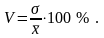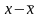5. Показатели вариации

Вариацией признака называется его изменение у единиц совокупности.

Показатели вариации – это показатели колеблемости вариант около средней величины.

Изучение вариации наряду с применением средних и относительных величин имеет большое практическое и научное значение. Например, данные о вариации возраста жителей в той или иной стране помогают охарактеризовать особенности возрастной структуры населения.

Вариация характеризует степень однородности совокупности по данному признаку.

Вариация присуща явлениям общества и природы.

Вариация существует в пространстве и во времени.

Значение показателей вариации заключается в следующем:

1. Показатели вариации дополняют средние величины, за которыми скрываются индивидуальные различия.

2. Показатели вариации характеризуют степень однородности статистической совокупности по данному признаку.

3. Показатели вариации характеризуют границы колеблемости признака.

4. Соотношение показателей вариации характеризует взаимосвязь между признаками.

1. Основные показатели вариации

Показатели вариации – это обобщающие показатели, которые измеряют вариацию в совокупности явлений.

В статистике применяются следующие показатели (меры) вариации:

• Размах вариации – R;

• Среднее линейное абсолютное отклонение - ;

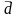• Дисперсия - ;

• Среднее квадратическое отклонение - ;

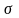• Коэффициент вариации – V.

Средние характеристики необходимо дополнять показателями, измеряющими отклонения от средних, показателями вариации признака.

1. Наиболее простым показателем вариации является показатель размаха вариации (R):

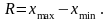
Размах вариации улавливает только крайние отклонения, но не отражает отклонений всех вариант в ряду распределения.

Пример 1. Имеются данные о выработке работников:

Порядковый № работника	Выработано за смену, дет.	Отклонение от средней выработки
	х
1 2 3 4 5	21 22 24 28 30	21 - 25 = - 4 - 3 - 1 + 3 + 5
Итого	125	0

Размах вариации представляет собой разность между максимальным и минимальным значениями признака:

дет.

2. Более точно отразит вариацию показатель, который исчисляется на базе всех значений признака в данной совокупности. Одним из таких показателей является среднее линейное отклонение ( ), которое представляет собой среднюю арифметическую из абсолютных значений отклонений вариант от средней величины:

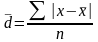
Для его определения необходимо исчислить среднюю величину по формуле средней арифметической простой:

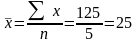дет.

Для того, чтобы дать обобщающую характеристику распределению следует исчислить «отклонение от средней», что означает разность между вариантой и средней арифметической в данной совокупности 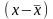. Данные отклонения приведены в таблице. Согласно свойству средней, положительные и отрицательные отклонения вариант от средней взаимно погашаются, т.е. .

Для примера среднее линейное отклонение имеет следующее значение:

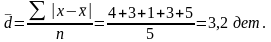
Среднее линейное отклонение бывает двух видов:

а) невзвешенное: ;

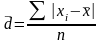б) взвешенное: .

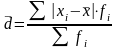Среднее линейное отклонение в статистике применяют очень редко.

3. Средний квадрат отклонения (дисперсия) - 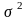часто применяется как в теории, так и в практике в качестве меры колеблемости признака.

Дисперсия бывает:

а) невзвешенной - ;

б) взвешенной - .

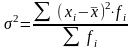4. Среднее квадратическое отклонение ( ) представляет собой корень квадратный из дисперсии.

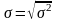
а) невзвешенное:

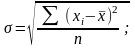
б) взвешенное:

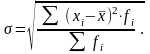
Учитывая, что среднее линейное отклонение и среднее квадратическое отклонение представляют собой абсолютные именованные величины, выраженные в тех же единицах измерения, что и варианты, для характеристики колеблемости признака используют относительные величины - коэффициенты.

1. Коэффициент вариации (V) – представляет собой отношение размаха вариации, среднего линейного отклонения или среднего квадратического отклонения к средней арифметической, выраженное в процентах (%) или в долях единицы.

а) Коэффициент осцилляции:

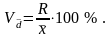
б) Линейный коэффициент вариации:

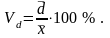
в) Коэффициент вариации: