
- •1.Числова функція. Область визначення і область значення функції. Способи задання функції
- •2. Графік функції. Найпростіші перетворення графіків функції
- •3) Властивості функцій. Монотонність функцій. Точки екстремуму функцій
- •1. Визначення Нехай безліч X - Це або безліч речових чисел , Або безліч комплексних чисел . Тоді послідовність елементів множини X називається числовою послідовністю.
- •5) Границя функції. Теореми про границі функції
- •Основні теореми про границі функцій
- •6) Тригонометричні функції числового аргументу. Основні співвідношення між тригонометричними функціями одного аргументу. Тригонометричні функції числового аргументу
- •Співвідношення між тригонометричними функціями одного аргументу
- •Формули зведення
- •8) Формули додавання. Формули зведення
- •8) Формули подвійного і половинного аргументу
- •Основні поняття, аксіоми, стереометрії та найпростіші наслідки з них
- •Взаємне розміщення двох прямих у просторі. Теореми про паралельні прямі
- •Паралельні прямі
- •Властивості паралельних прямих
- •Ознаки паралельності прямих
- •Паралельне проектування і його властивості. Зображення фігур в стереометрії
- •Паралельність площин. Ознака паралельності двох площин. Теорема про паралельні площини.
- •2. Аналітичне визначення
- •Ознака паралельності площин
- •Властивості паралельних площин
- •Перпендикулярність прямих у просторі. Теорема про перпендикулярні прямі
- •Перпендикулярність прямої і площин
- •Перпендикуляр і похила. Теорема про три перпендикуляри.
- •Властивості похилих, проведених з однієї точки до однієї площини
- •Перпендикулярність площин. Ознака перпендикулярність двох площин
- •Ознака перпендикулярності площин
- •Вимірювання відстаней у просторі
- •Вимірювання кутів у просторі
- •Вектори у просторі. Дії над вектором.
- •. Прямокутна система координат у просторі. Координати вектора. Дії над векторами, заданими своїми координатами
Паралельність площин. Ознака паралельності двох площин. Теорема про паралельні площини.
Якщо площину α паралельна кожній з двох пересічних прямих, що лежать в іншій площині β, то ці площини паралельні
Якщо дві паралельні площини пересічені третьої, то лінії їх перетину паралельні
Через точку поза даною площині можна провести площину, паралельну даної, і притому тільки одну
Відрізки паралельних прямих, обмежені двома паралельними площинами, рівні
Два кута з відповідно паралельними і однаково спрямованими сторонами рівні і лежать у паралельних площинах
2. Аналітичне визначення
Якщо площині
![]() і
і ![]()
паралельні,
то нормальні
вектори ![]() і
і ![]() колінеарні (і
назад). Тому умова
колінеарні (і
назад). Тому умова
Ознака паралельності площин
Теорема
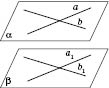
1. Якщо дві прямі однієї площини, які
перетинаються й відповідно паралельні
двом прямим другої площини (див. рисунок),
то ці площини паралельні.
 Теорема
2 (обернена). Якщо в одній площині є дві
прямі, які перетинаються, і ці прямі
паралельні другій площині, то такі
площини паралельні.
Зверніть
увагу: прямі мають обов’язково
перетинатися. Дійсно, в площині
може
бути скільки завгодно прямих, паралельних
прямій a (див.
рисунок нижче), а значить, і площині
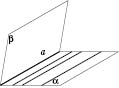
Теорема
2 (обернена). Якщо в одній площині є дві
прямі, які перетинаються, і ці прямі
паралельні другій площині, то такі
площини паралельні.
Зверніть
увагу: прямі мають обов’язково
перетинатися. Дійсно, в площині
може
бути скільки завгодно прямих, паралельних
прямій a (див.
рисунок нижче), а значить, і площині ![]() ,
і при цьому площини
і
не
будуть паралельними.
,
і при цьому площини
і
не
будуть паралельними.
 Теорема
3. Якщо пряма перетинає одну з двох
паралельних площин, то вона перетинає
й другу (див. рисунок).
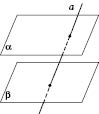
Теорема
3. Якщо пряма перетинає одну з двох
паралельних площин, то вона перетинає
й другу (див. рисунок).
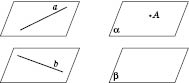
 Теорема
4. Через дві мимобіжні прямі можна
провести паралельні площини (рисунок
нижче зліва).
Теорема
5. Через точку поза даною площиною можна
провести площину, паралельну даній, і
до того ж тільки одну (рисунки
нижче).
Теорема
4. Через дві мимобіжні прямі можна
провести паралельні площини (рисунок
нижче зліва).
Теорема
5. Через точку поза даною площиною можна
провести площину, паралельну даній, і
до того ж тільки одну (рисунки
нижче).
 Теорема
6. Якщо дві площини паралельні третій,
то вони паралельні одна одній. [1] є
необхідна і достатня умова паралельності
або збігу.
Теорема
6. Якщо дві площини паралельні третій,
то вони паралельні одна одній. [1] є
необхідна і достатня умова паралельності
або збігу.
Властивості паралельних площин
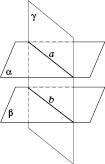 Теорема
1. Якщо дві паралельні площини перетинаються
третьою площиною (див. рисунок), то прямі
перетину паралельні.
На
рисунку:
Теорема
1. Якщо дві паралельні площини перетинаються
третьою площиною (див. рисунок), то прямі
перетину паралельні.
На
рисунку: ![]() ;
.
;
.
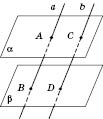 Теорема
2. Відрізки паралельних прямих, які
містяться між двома паралельними
площинами (див. рисунок), рівні. На
рисунку:
;
;
Теорема
2. Відрізки паралельних прямих, які
містяться між двома паралельними
площинами (див. рисунок), рівні. На
рисунку:
;
; ![]() .
.
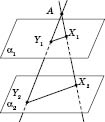 Теорема
3. Нехай площини
Теорема
3. Нехай площини ![]() і
і ![]() паралельні
(див. рисунок нижче) і є точка A,
яка не лежить у жодній із цих площин.
Через точку A проведено
довільну пряму. Нехай
паралельні
(див. рисунок нижче) і є точка A,
яка не лежить у жодній із цих площин.
Через точку A проведено
довільну пряму. Нехай ![]() і
і ![]() —
точки перетину прямої з площинами
і
.
Відношення довжини відрізків
—
точки перетину прямої з площинами
і
.
Відношення довжини відрізків ![]() не
залежить від узятої прямої (AY1
: AY2
= AX1
: AX2).
не
залежить від узятої прямої (AY1
: AY2
= AX1
: AX2).
Перпендикулярність прямих у просторі. Теорема про перпендикулярні прямі
Дві прямі на площині називаються перпендикулярними, якщо при перетині вони утворють 4 прямих кути. Дві прямі називаються перпендикулярними, якщо вони перетинаються під прямим кутом. Теорема 1. Якщо дві прямі, які перетинаються, паралельні відповідно двом іншим перпендикулярним прямим, то інші прямі теж перпендикулярні. Теорема 2. Через будь-яку точку прямої у просторі можна провести безліч перпендикулярних до неї прямих (див. рисунок). (Усі прямі лежать у площині, яка перпендикулярна до даної прямої і перетинає її у даній точці.)
В
аналітичному вигляді прямі, задані
лінійними функціями ![]() и
и ![]() будуть
перпендикулярними, якщо виконується
умова
будуть
перпендикулярними, якщо виконується
умова ![]() .
(Тут
.
(Тут ![]() —
кути нахилу прямої до горизонталі)
—
кути нахилу прямої до горизонталі)
Дві площини називаються перпендикулярними, якщо двогранний кут між ними дорівнює 90 градусам. Теорема 1. Якщо дві прямі, які перетинаються, паралельні відповідно двом іншим перпендикулярним прямим, то інші прямі теж перпендикулярні. Теорема 2. Через будь-яку точку прямої у просторі можна провести безліч перпендикулярних до неї прямих (див. рисунок). (Усі прямі лежать у площині, яка перпендикулярна до даної прямої і перетинає її у даній точці.)
Через будь-яку точку в просторі, що не належить даній прямій, можна провести пряму, перпендикулярну до даної, і тільки одну. Це буде та перпендикулярна до даної прямої пряма, яка лежить у площині, визначеній даними прямою й точкою:
Зверніть увагу, що в просторі дві прямі, перпендикулярні до однієї і тієї самої прямої, не обов’язково паралельні між собою. На рисунку ; .
Пряма, яка перетинає площину, називається перпендикулярною до цієї площини, якщо вона перпендикулярна до будь-якої прямої, що лежить у цій площині й проходить через точку перетину (див. рисунок).
Теорема 3. Якщо пряма перпендикулярна до двох прямих, які лежать у площині й перетинаються, то вона перпендикулярна до даної площини (див. рисунок).
Зверніть увагу: якщо пряма перпендикулярна до однієї прямої площини, то цього не досить для перпендикулярності прямої і площини. На рисунку , але a не перпендикулярна до , зокрема a не перпендикулярна до с.
Теорема 4. Через точку, яка не належить даній площині, можна провести пряму, перпендикулярну до даної площини, і тільки ¬одну. Теорема 5. Через дану точку площини можна провести одну, й тільки одну, перпендикулярну до неї пряму. Теорема 6. Через дану точку прямої можна провести одну, й тільки одну, перпендикулярну до неї площину. Теорема 7. Через точку, яка не лежить на прямій, можна провести одну, й тільки одну, площину, перпендикулярну до даної прямої. Теорема 8. Якщо площина перпендикулярна до однієї з двох паралельних прямих, то вона перпендикулярна й до другої. Теорема 9. Дві прямі, перпендикулярні до однієї й тієї самої площини, паралельні між собою.
