1. Визначення Нехай безліч X - Це або безліч речових чисел , Або безліч комплексних чисел . Тоді послідовність елементів множини X називається числовою послідовністю.

Границя числової послідовності — фундаментальне поняття математичного аналізу, число, до якого члени послідовності прямують зі збільшенням індекса в сенсі наступного означення:

Дійсне число a називається границею числової послідовності  , якщо  ^[1]

Позначення:   або 

При цьому також кажуть, що послідовність   збігається до числа a, або має границю a. Послідовність, що збігається до деякої границі називається збіжною, в інших випадках — розбіжною.

5) Границя функції. Теореми про границі функції

Нехай функція   визначена у всіх точках проміжку  , за винятком, можливо, деякої точки  . Побудуємо послідовність значень аргументу функції  :

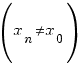,    , (1)

таку, щоб всі члени послідовності належали проміжку   і послідовність збігалась до точки  :

.

Тоді значення функції 

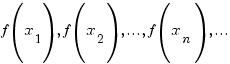. (2)

також утворять деяку числову послідовність.

Говорять, що число   є границею функції   при  , що прямує до  , якщо для будь-якої послідовності значень аргументу (1), яка збігається до числа  , послідовність значень функції (2) збігається до числа  , і пишуть

.

Примітка. Це визначення границі функції називається визначенням границі по Гейне.

Існує й інше, еквівалентне тому, що вище, визначення границі функції.

Говорять, що число   є границею функції   при  , що прямує до  , якщо для будь-якого додатнього числа   знайдеться таке додатне число  , яке залежить від  , що при всіх  , які задовільняють нерівність

,

виконується нерівність

.

Примітка. Це визначення границі функції називається визначенням границі по Коші.

Основні теореми про границі функцій

Теорема 1. Якщо функції   і   в точці   мають границі, то сума і добуток цих функцій також мають у цій точці границю, причому ; . Теорема 2. Якщо функції   і   в точці   мають границі й  , то й функція  має в цій точці границю, яка дорівнює . Теорема 3. Якщо при   функція   має границю A, то ця границя єдина. Приклади 1) . 2) . Зверніть увагу: скоротити дріб на   можна, тому що в означенні границі  . 3)  — перша визначeна границя. 4) . 5) . Урахуємо, що  , а функція   є обмеженою

6) Тригонометричні функції числового аргументу. Основні співвідношення між тригонометричними функціями одного аргументу. Тригонометричні функції числового аргументу

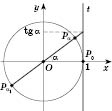
Розглянемо одиничне (тригонометричне) коло, центр якого розташований у точці   і радіус якого дорівнює 1 (див. рисунок). 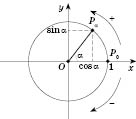Нехай точка P0 — це точка (1; 0). Кожну іншу точку кола можна дістати поворотомP0 навколо початку координат. Будемо вважати від’ємним напрямок повороту за годинниковою стрілкою, додатним — проти. Точку, яку дістанемо поворотом P0 навколо початку координат на кут  , назвемо  . Очевидно, що значення   можуть бути від   до  , причому кути, міри яких відрізняються на  ,  , дають на колі одну й ту саму точку. Наприклад: ,  . Введемо означення: ;  ; ;  . Значення  ,  ,  ,   залежить тільки від кута  . Для   ці означення дають той самий результат, що й означення за допомогою елементів прямокутного трикутника. Якщо означення  ,  ,  ,   уведені таким чином, то очевидно, що ми дістали числові функції. Дійсно, кожному значенню   відповідає єдине значення   і  . Також кожному дійсному значенню  ,  , відповідає єдине значення   і кожному значенню  , , відповідає єдине значення  . Проведемо дотичну t до одиничного кола в точці   (див. рисунок нижче). Вона називається лінією тангенсів, тому що ордината точки перетину прямої   із прямою t дорівнює тангенсу кута    . 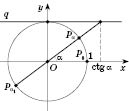Проведемо дотичну q до одиничного кола в точці   (див. рисунок на с. 73). Для довільного числа  , , абсциса точки перетину прямої   з прямою q дорівнює котангенсу кута  . Тому пряма q називається лінією котангенсів.