3.2 Алгоритм поворота изображения

На сканированном изображении нотный стан вместе со всеми элементами на нем, может сместиться на некоторый угол относительно своего первоначально положения на исходном изображении. Поэту необходимо реализовать метод поворота изображения, дабы облегчить задачу распознавания нот. Потребуется найти и рассчитать угол отклонения относительно верхней границы изображения либо относительно левого края изображения. Для решения этой проблемы можно обратиться к свойствам прямоугольного треугольника, так как, если провести прямую линию от верхнего угла отклонившегося нотного стана и прямую от второго угла, который ниже первого угла, получается прямоугольный треугольник. Пример приведен на рисунке 3.2.1.

Рисунок 3.2.1 – Пример аналогии отклонённого нотного стана и прямоугольно треугольника

Из рисунка 3.2.1 можно заметить, что верхняя линия нотного стана является гипотенузой прямоугольного треугольника, а две линии проведенных из верхнего и нижнего углов нотного стана – катетами.

Для поворота изображения используется функция C#, входными параметрами которой являются изображение и угол, на который будет происходить поворот картинки. Для того, чтобы найти угол поворота требуется высчитать длину двух катетов, которые являются прямыми проведенные из верхнего и нижнего угла первой полосы нотного стана.

Рисунок 3.2.3 – Искомый угол поворота изображения

Где С – гипотенуза треугольника, а также первая полоса нотного стана;

 - искомый угол поворота;

x1,x2 – нижняя и верхняя точки первой полосы нотного стана;

b, c – катеты прямоугольника;

Значение длины катета а = х2.х – х1.х. Значение длины катета b = х1.у – х2.у. Для нахождения гипотенузы следует воспользоваться теоремой Пифагора. Значение  = arcsin(sin) = arcsin(b/c).

Рисунок 2.3.4 – Входное перевернутое изображение

Рисунок 2.3.5 – Выходное изображение после поворота

3.3 Алгоритм сегментации нотного стана

Задача выделения нотного стана сводиться к нахождению верхних и нижних граней строк стана, изображённого на исходной картинке. Алгоритм сегментации основывается на том, что средняя яркость в изображениях межполосных промежутках существенно ниже средней яркости в изображениях строк нотного стана.

Сначала для всех пиксельных строк исходного изображения находится их средние значения яркости, согласно формуле: .

Затем определяем среднее значение яркости всего изображения, согласно формуле: .

Средняя яркость в межполосных промежутках нотного стана должна быть невелика. Поэтому яркость верхней границы полосы нотного стана можно выразить через среднюю яркость изображения: S^t=k^t*S(B), где 0<k^t<1 – коэффициент.

Аналогично яркость нижней границы полосы нотного стана, также может быть выражена через среднюю яркость всего изображения: S^b=k^b*S(B), где 0<k^b<1 – коэффициент.

Работа алгоритма сегментации строк заключается в последовательном просмотре массива средних значений (s₁,...,s_m) и выявлении множества пар индексов (s^t_i,s^b_i) пиксельных строк, соответствующих верхней s^t_i и нижней s^b_i граням изображения строки номер i.

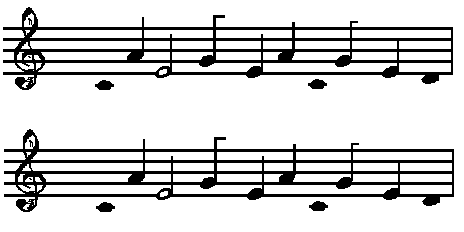
Рисунок 3.3.1 – Результат сегментации нотного стана.

3.4 Алгоритм сегментации скрипичного ключа

Для сегментации скрипичного ключа был разработан алгоритм. Находится первый верхний черный пиксель с левой стороны изображения, затем находится первый нижний черный пиксель с левой стороный изображения (рис. 3.4.1)

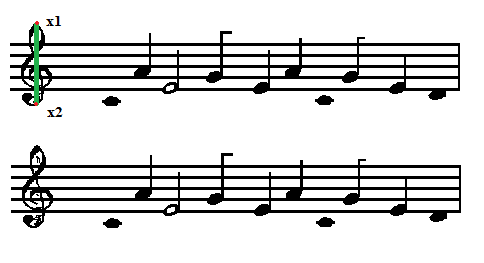
Рисунок 3.4.1 – Нахождение верхней и нижней точки скрипичного ключа

После того, как были найдены верхнии и нижнии точки скрипичного ключа, находится высота скрипичного ключа. Так как у каждой точки есть кординаты по оси х и у, то высота скрипичного ключа h = x2.y-x1.y. Далее находится ширина скрипичного ключа, w= h/2. После этого, в прямоугольнике с размером w на h просматривается каждый пискель и проверяется его цвет, если он черный, то в данном пикселе устанавливается желтый цвет, иначе цвет остается неизменнным.

Рисунок 3.4.2 – Результат сегментирования скрипичного ключа