1.1.4.Приведение матричной игры к задаче линейного программирования

Обозначим через S_A=(p₁, p₂, …, p_n) оптимальную смешанную стратегию игрока A. Требуется найти вероятности и определить цену игры при условии, что известна платёжная матрица игры. Допустим, что игрок B выбирает чистую стратегию B₁. Тогда средний выигрыш для игрока A будет равен a₁₁p₁+a₂₁p₂+…+a_n1p_n. Этот выигрыш должен быть не меньше цены игры v, следовательно, a₁₁p₁+a₂₁p₂+…+a_n1p_n≥v.

Если игрок B выберет стратегию B₂, то и в этом случае средний выигрыш игрока A должен быть не меньше цены игры v, следовательно, a₁₂p₁+a₂₂p₂+…+a_n2p_n≥v.

Какую бы стратегию ни выбирал игрок B, выигрыш игрока A всегда должен быть не меньше цены игры v. Поэтому мы можем записать следующую систему из m неравенств (напоминаем, что m — число чистых стратегий игрока B):

a ₁₁p₁+a₂₁p₂+…+a_n1p_n≥v;

a₁₂p₁+a₂₂p₂+…+a_n2p_n≥v;

………………………… (1)

a_1mp₁+a_2mp₂+…+a_nmp_n≥v.

При этом p₁+p₂+…+p_n=1. (2)

Введя обозначения x₁=p₁/v, x₂=p₂/v, … x_n=p_n/v, перепишем (1) и (2) в виде

a ₁₁x₁+a₂₁x₂+…+a_n1x_n≥1;

a₁₂x₁+a₂₂x₂+…+a_n2x_n≥1;

………………………… (3)

a_1mx₁+a_2mx₂+…+a_nmx_n≥1;

x₁+x₂+…+x_n=1/v. (4)

Нам желательно, чтобы цена игры была максимальной, следовательно, 1/v должна быть минимальной. Таким образом, поиск оптимальной смешанной стратегии свёлся к решению следующей задачи линейного программирования: надо найти неотрицательные величины x_i такие, чтобы они удовлетворяли неравенствам (3) и обращали в минимум сумму x₁+x₂+…+x_n, т.е.

L= x₁+x₂+…+x_n→min,

при ограничениях

a ₁₁x₁+a₂₁x₂+…+a_n1x_n≥1;

a₁₂x₁+a₂₂x₂+…+a_n2x_n≥1;

…………………………

a_1mx₁+a_2mx₂+…+a_nmx_n≥1;

x_i≥0, i=1, 2, …, n/

Задача. Самолёты против зениток. Найдём оптимальную смешанную стратегию некоторой конкретной игры. Предположим, что сторона A нападает на сторону B. У стороны A имеются два самолёта, несущие мощное поражающее средство. У стороны B имеются четыре зенитки, при помощи которых осуществляется оборона важного объекта. Чтобы объект оказался разрушенным, достаточно, чтобы к нему прорвался хотя бы один самолёт. Для подхода к объекту самолёты могут выбрать любой из четырёх воздушных коридоров (см. рис. 2).

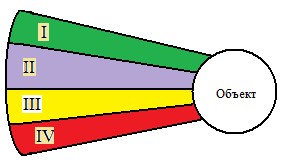
Рис. 2. Воздушные коридоры и объект

У стороны A есть две чистые стратегии: стратегия A₁ — самолёты посылаются в разных воздушных коридорах (безразлично, каких именно), стратегия A₂ — оба самолёта посылаются в каком-то одном из коридоров. Возможные стратегии стороны B таковы: B₁ — поставить по зенитке на каждый коридор, B₂ — поставить по две зенитки на какие-то два коридора (остальные два коридора остаются неохраняемыми, B₃ — поставить две зенитки на один из коридоров и по одной зенитке ещё на два коридора, B₄ — поставить три зенитки на один из коридоров и одну зенитку ещё на один коридор, B₅ — поставить все четыре зенитки на один из коридоров. Стратегии B₄ и B₅ заведомо невыгодны хотя бы потому, что три, а тем более четыре зенитки в пределах одного коридора не нужны, ведь у стороны A всего два самолета. Поэтому ограничимся стратегиями B₁, B₂, B₃.

Предположим, что сторона A выбрала стратегию A₁, сторона B — стратегию B₁. Ясно, что тогда ни один самолёт не прорвётся к объекту — выигрыш стороны есть нуль (a₁₁=0). Пусть выбраны стратегии A₁ и B₂. В этой ситуации, какие бы два коридора ни выбирала сторона B для размещения пар зениток, у самолётов всегда будут шесть равновероятных вариантов и только один проигрышный. Таким образом, при выборе стратегий A₁ и B₂ вероятный выигрыш стороны A составляет 5/6 (a₁₂=5/6). Рассуждая подобным образом, найдём остальные элементы платёжной матрицы данной игры (см. табл. 6). Нижняя цена игры равна ½, верхняя ¾. Седловой точки нет, оптимальное решение лежит в области смешанных стратегий.

Табл. 6. Платёжная матрица игры

B A	В1	В2	В3	min
А1	0	5/6	1/2	0
А2	1	1/2	3/4	1/2
max	1	5/6	3/4

Чтобы найти оптимальную смешанную стратегию, воспользуемся платёжной матрицей (см. табл. 6) и соотношениями (3) и (4). В результате получим следующую задачу линейного программирования:

x₁+x₂→min

, x₁≥0, x₂≥1

Решение удобно представить графически. Для этого построим область допустимых решений D (см. рис. 3). Уравнение x₁+x₂=const описывает семейство параллельных прямых, которые на рисунке показаны штриховыми линиями. Из всех прямых, имеющих хотя бы одну точку в пределах допустимой области, наименьшей сумме x₁+x₂ соответствует прямая FF. Точка G соответствует оптимальной смешанной стратегии. Координаты этой точки: x₁=3/5; x₂=1. Отсюда v=5/8, p₁=3/8, p₂=5/8. Итак, оптимальная смешанная стратегия стороны A предполагает использование стратегии A₁ с вероятностью 3/8 и стратегии A₂ с вероятностью 5/8.

Как воспользоваться этой рекомендацией на практике? Если игра происходит один раз, то стороне A следует, по-видимому, избрать стратегию A₂, ведь p₂>p₁. Предположим, что игра совершается многократно (например, по отношению к многим объектам, подлежащим бомбардировке). Если игра повторяется раз N (N»1), то в 3N/8 случаях сторона A должна избрать стратегию A₁, а в 5N/8 случаях стратегию A₂.

Рассмотрим поведение стороны B. При выборе стороной A оптимальной смешанной стратегии её средний выигрыш оказывается в пределах между верхней ценой игры, раной ¾, и ценой игры v=5/8. При неразумном поведении стороны B выигрыш стороны A может оказаться равным верхней цене игры (и даже может стать больше). Если сторона B, в свою очередь, будет придерживаться

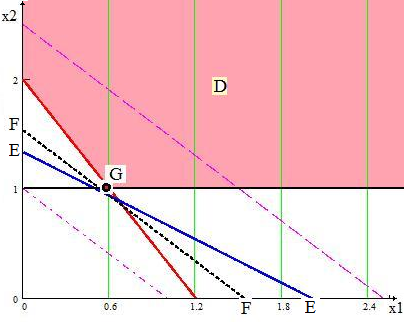
Рис. 3. Допустимая область D (область красного цвета) и решение G.

оптимальной смешанной стратегии, то выигрыш игрока A окажется равным цене игры v. Оптимальная смешанная стратегия стороны B сводится к тому, что эта сторона вообще не применяет стратегию B₃, стратегию B₁ использует с вероятностью ¼, а стратегию B₂ с вероятностью ¾. Нецелесообразность применения стратегии B₃ усматривается из рисунка: соответствующая этой стратегии прямая EE не имеет общих точек с красной областью. Для определения вероятностей, с какими должны использоваться стратегии B₁ и B₂, воспользуемся уже найденным значением цены игры (v=5/8): q₁0+q₂5/6=5/8. Отсюда видно, что q₁=1/4, q₂=3/4. [Тарасов Л. В. Мир, построенный на вероятности. – М.: Просвещение, 1984. – 191 с.].

При решении произвольной конечной игры размера n × m рекомендуется придерживаться следующей схемы:

1. Исключить из платежной матрицы заведомо невыгодные стратегии по сравнению с другими стратегиями. Такими стратегиями для игрока А (игрока В) являются те, которым соответствуют строки (столбцы) с элементами, заведомо меньшими (большими) по сравнению с элементами других строк (столбцов).

2. Определить верхнюю и нижнюю цены игры и проверить, имеет ли игра седловую точку. Если седловая точка есть, то соответствующие ей стратегии игроков будут оптимальными, а цена совпадает с верхней (нижней) ценой.

3. Если седловая точка отсутствует, то решение следует искать в смешанных стратегиях. Для игр размера m × n рекомендуется симплексный метод, для игр размера 2×2, 2×m, m×2 возможно геометрическое решение.

Фактическое решение некоторых классов антагонистических игр сводится к решению дифференциальных и интегральных уравнений, а матричных игр — к решению стандартной задачи линейного программирования. Разрабатываются приближённые и численные методы решения игр. Для многих игр оптимальными оказываются так называемые смешанные стратегии, то есть стратегии, выбираемые случайно (например, по жребию).

Теория игр, созданная для математического решения задач экономического и социального происхождения, не может в целом сводиться к классическим математическим теориям, созданным для решения физических и технических задач. Однако в различных конкретных вопросах теория игр широко используются весьма разнообразные классические математические методы. Кроме этого, теория игр связана с рядом математических дисциплин внутренним образом. В теория игр. систематически и по существу употребляются понятия теории вероятностей. На языке теория игр можно сформулировать большинство задач математической статистики. Необходимость при анализе игры количественного учёта неопределённости предопределяет важность и тем самым связь И. т. с теорией информации и через её посредство — с кибернетикой. Кроме того, теория игр, будучи теорией принятия решений, может рассматриваться как существенная составная часть математического аппарата операций исследования.

Теория игр применяется в экономике, технике, военном деле и даже в антропологии. Основные трудности практического применения теория игр связаны с экономической и социальной природой моделируемых ею явлений и недостаточным умением составлять такие модели на количественном уровне.