Пересечение поверхности с прямой линией

Подробнее…/Почуева Ю. А. Поверхности (стр. 14 – 30)

С л у ч а й 1. Прямая линия — проецирующая прямая,

кривая поверхность — непроецирующая

Задачи

39. Определить точки пересечения прямой (АВ) с заданными поверхностями (рис.60). Установить видимость на эпюре.

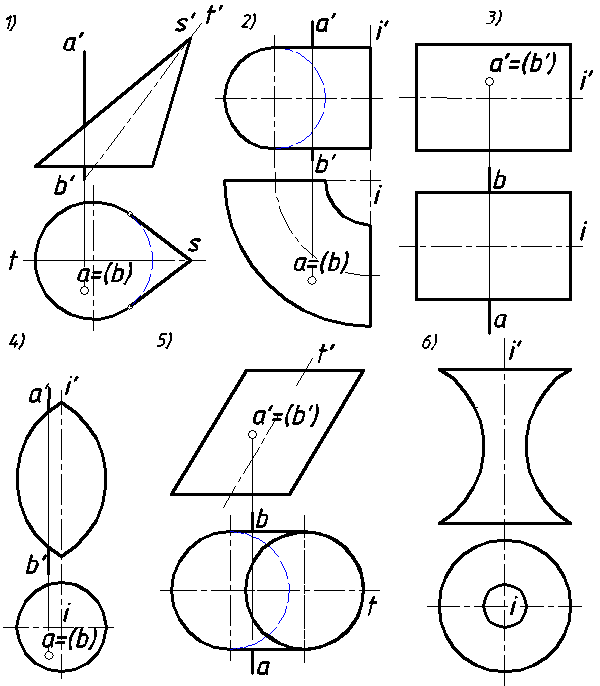
Рис. 60.

С л у ч а й 2. Поверхность — проецирующая,

прямая — непроецирующая

Проецирующими являются любые цилиндрические поверхности, образующие которых перпендикулярны какой-либо плоскости проекций, и призматические поверхности, ребра которых являются проецирующими прямыми.

Задачи

40. Определить точки пересечения прямой (АВ) с заданными поверхностями :

1) прямого кругового цилиндра;

2) эллиптического цилиндра;

3) прямой треугольной призмы.

Установить видимость на эпюре (рис. 61).

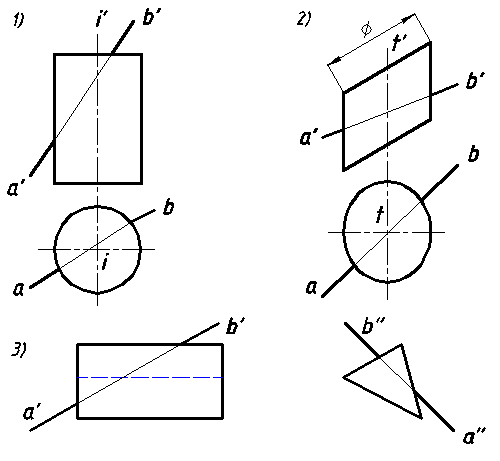
Рис. 61.

С л у ч а й 3. Кривая поверхность и линия не являются проецирующими

Задачи такого рода решаются по алгоритму. (См . Почуева Ю. А. Поверхности стр. 47).

Задачи

41. Определить точки пересечения прямой (АВ) с заданными поверхностями :

1) отсека открытого тора;

2) кругового конуса;

3) открытого тора.

Установить видимость на эпюре (рис. 62).

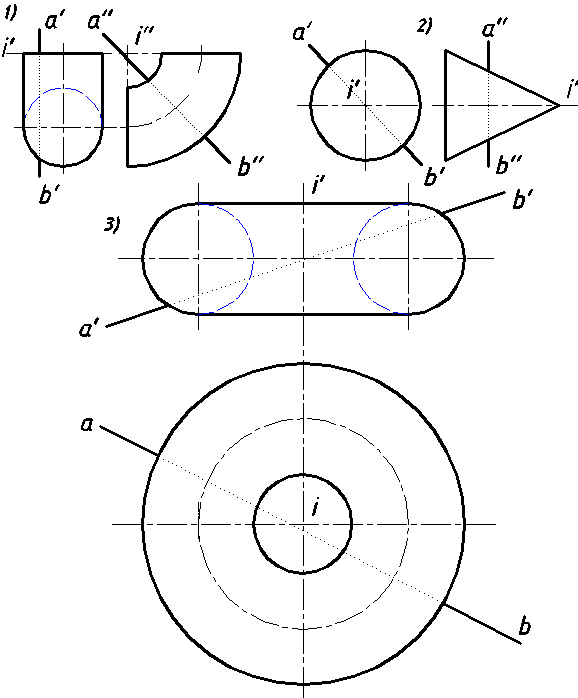
Рис. 62.

Пересечение кривых поверхностей

Рассмотрим случай, когда одна из заданных поверхностей — проецирующая.

Примечание. В этом случае задача по определению линии пересечения поверхностей сводится к умению брать точку на непроецирующей поверхности. Подробнее…/Почуева Ю. А. Поверхности (стр. 60 – 69)

Задачи

42. Построить линию пересечения заданных поверхностей. Установить их взаимную видимость на эпюре (рис. 63).

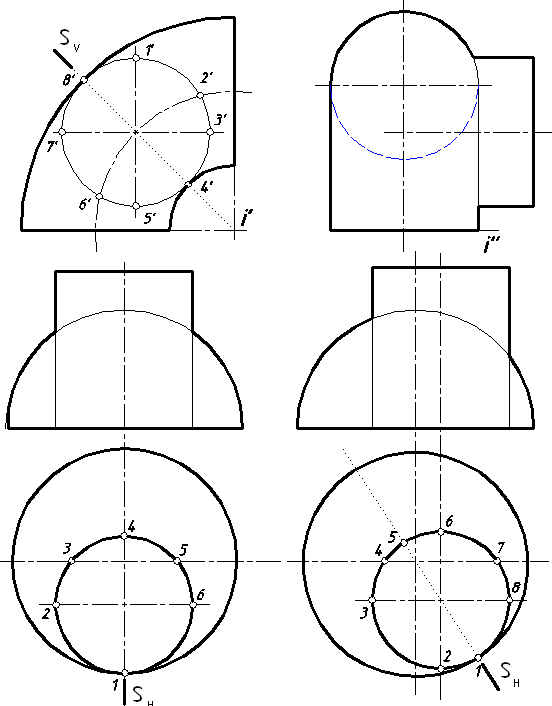
Рис. 63.

Пересечение кривых поверхностей

Применение вспомогательных поверхностей – посредников.

Способ вспомогательных секущих плоскостей

Подробнее…/Почуева Ю. А. Поверхности Стр. 72 – 80

Задачи

43. Построить линию пересечения заданных поверхностей. Установить их взаимную видимость на эпюре (рис. 64).

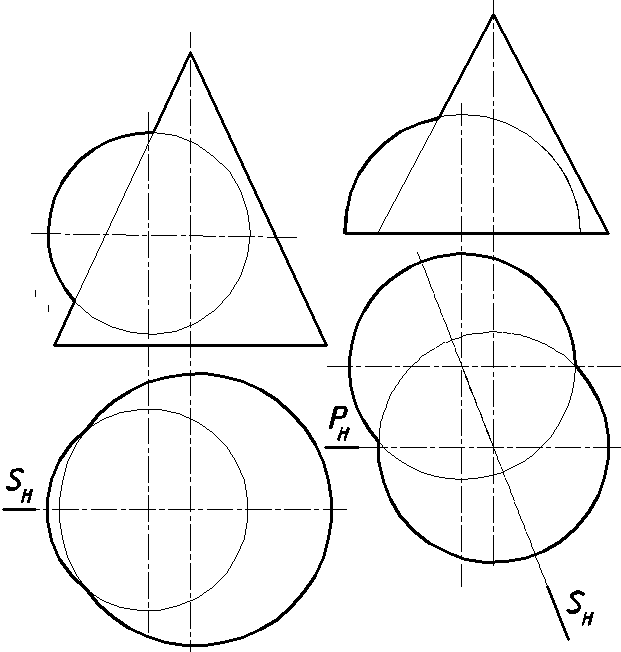
S — общая плоскость симметрии заданных поверхностей;

P — граница видимости точек искомой линии пересечения на фронтальной проекции

Рис. 64.

Способ вспомогательных концетрических сфер

Подробнее…/Почуева Ю. А. Поверхности Стр. 77 – 80

Лемма. Соосные поверхности вращения пересекаются по окружности столько раз, сколько пересекаются их главные полумеридианы.

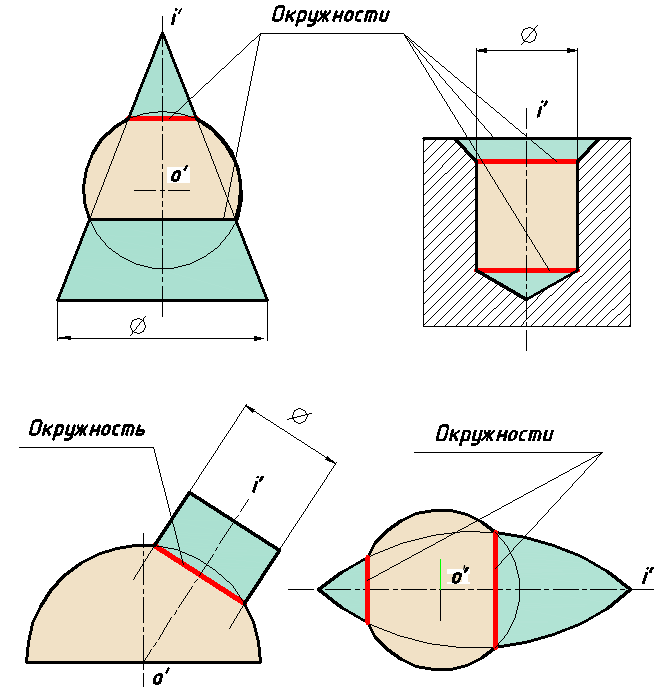
Рис. 65.

На рис. 65 приведены примеры применения леммы.

Задачи

44. Построить линию пересечения заданных поверхностей. Установить их взаимную видимость на эпюре (рис. 66).

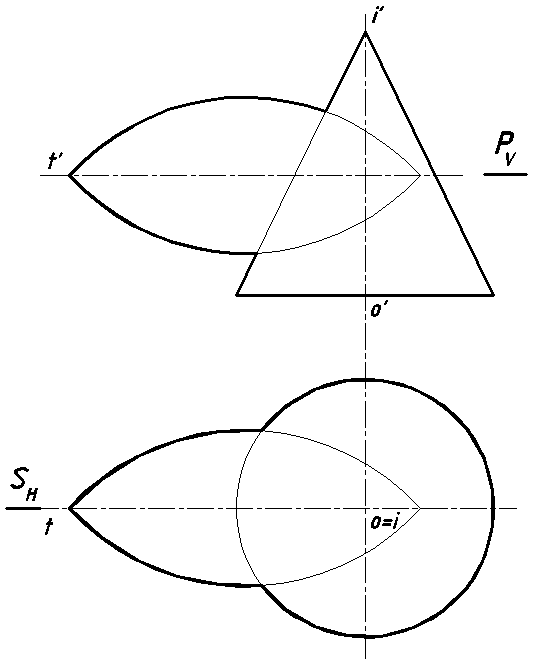
Рис. 66.

I ∩ T = O

S — общая плоскость симметрии заданных поверхностей;

P — граница видимости точек искомой линии пересечения на горизонтальной проекции

45. Построить линию пересечения заданных поверхностей. Установить их взаимную видимость на эпюре (рис. 67).

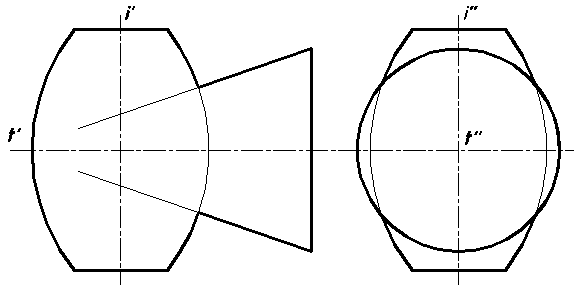
Рис. 67.

С разделами Циклические поверхности и Способ эксцентрических сфер ознакомиться самостоятельно ./ Почуева Ю. А. Поверхности Стр. 90– 97