Прямые общего и частного положения

Прямая, не параллельная и не перпендикулярная ни к одной из плоскостей проекций — прямая общего положения (рис. 8).

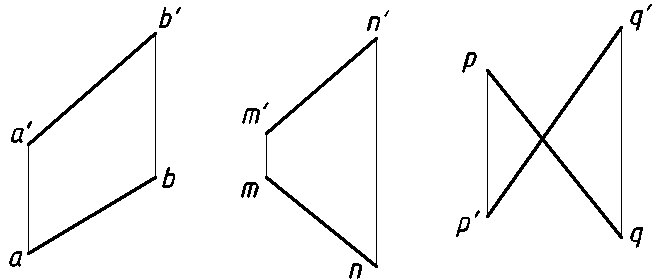
Рис. 8

Прямые частного положения делятся на две группы:

1) проецирующие прямые — прямые, перпендикулярные какой-либо плоскости проекций (рис. 9):

а) прямая, перпендикулярная плоскости Н — горизонтально-проецирующая прямая;

б) прямая, перпендикулярная плоскости V — фронтально-проецирующая прямая;

в) прямая, перпендикулярная плоскости W — профильно-проецирующая прямая

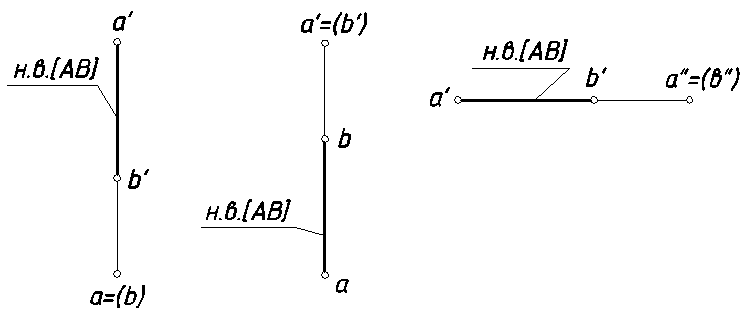
Рис. 9.

2) прямые уровня — прямые, параллельные какой-либо плоскости проекций (рис.10):

а) прямая, параллельная плоскости Н — горизонтальная прямая;

б) прямая, параллельная плоскости V — фронтальная прямая;

в) прямая, параллельная плоскости W — профильная прямая

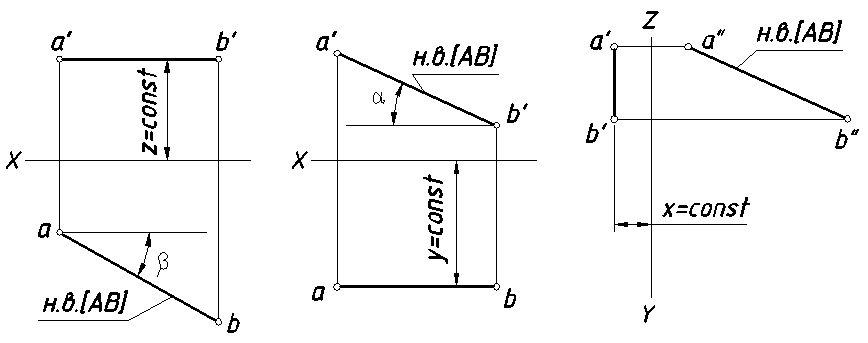
Рис.10.

Прямая. Взаимное положение прямых. Задачи

7. Определить взаимное положение отрезков прямых [AB] и [CD], ответы записать в строки 1), 2), 3) и 4) математическими символами (рис. 11).

.

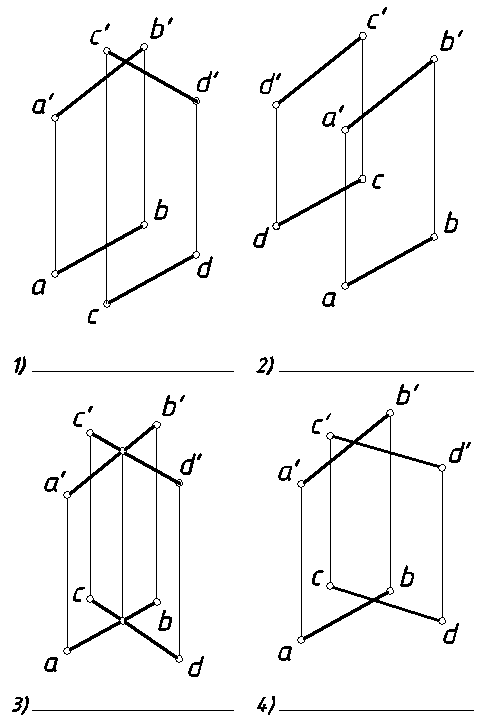
Рис. 11.

8. Через точку С провести прямую, параллельную отрезку [AB] и горизонтальную прямую, пересекающую данный отрезок (рис. 12).

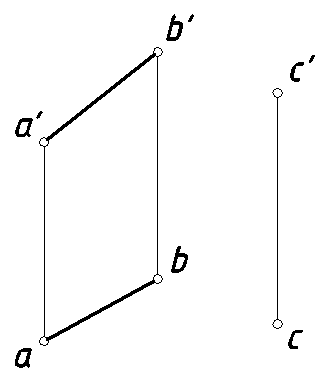
Рис. 12.

9. Через точку С провести прямую, параллельную плоскости H и пересекающую ось Z (рис. 13).

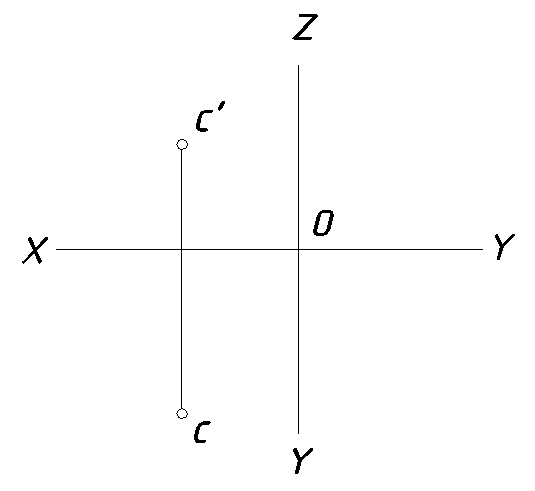
Рис. 13.

Основные задачи на прямую:

1) Деление отрезка прямой в заданном отношении (осуществляется на основании теоремы Фалеса);

2) Нахождение натуральной величины отрезка прямой общего положения (способ прямоугольного треугольника)

Задачи

10. Разделить отрезок [AB] в отношении 1:2, а отрезок [CD] в отношении m:n (рис. 14).

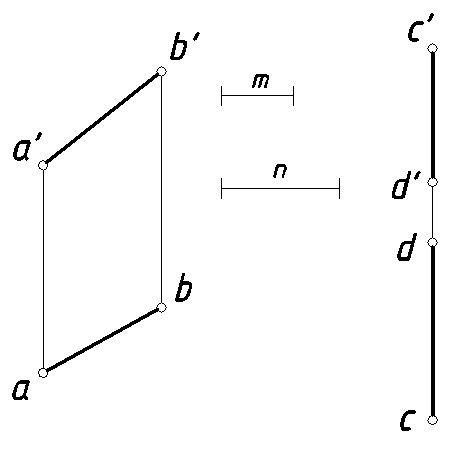
Рис. 14.

11. Построить усеченную пирамиду так, чтобы верхнее основание делило боковые ребра полной пирамиды в отношении 2 : 3, начиная от ее вершины (рис. 15).

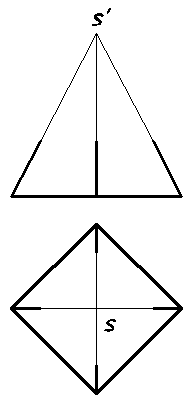
Рис.15.

Правило прямоугольного треугольника

Для нахождения натуральной величины отрезка прямой общего положения необходимо построить прямоугольный треугольник, одним катетом которого является горизонтальная (фронтальная) проекция отрезка, а другим разность высот (глубин) концов отрезка. Гипотенуза построенного треугольника будет являться натуральной величиной отрезка (рис. 16).

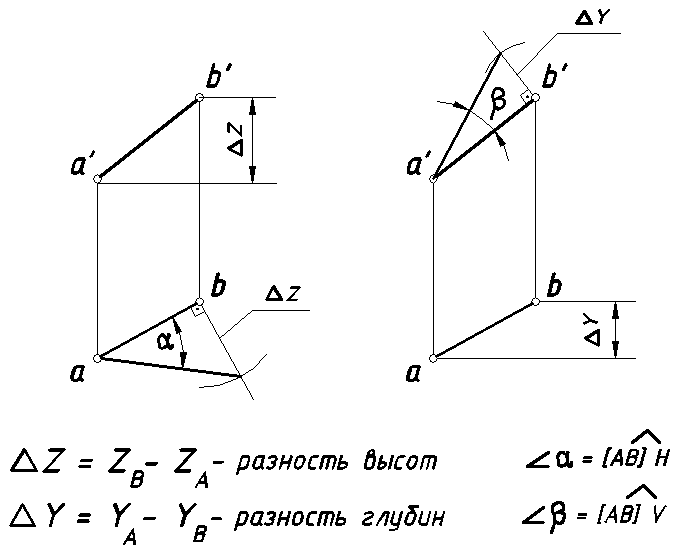
Рис. 16.

Задачи

12. Построить фронтальную проекцию отрезка [AB], составляющего с плоскостью H угол 30◦. Сколько решений имеет задача? (рис. 17).

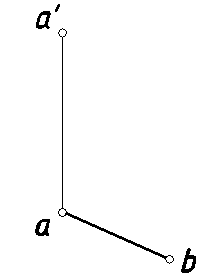
Рис. 17.

13. Построить горизонтальную проекцию отрезка [АВ], длина которого 60 мм. Определить угол наклона отрезка [АВ] к плоскости проекций V (рис. 18).

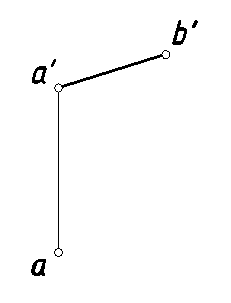
Рис. 18.

Теорема о частном проецировании прямого угла она плоскость

Если одна сторона прямого угла параллельна какой-либо плоскости, а другая не перпендикулярна ей – прямой угол проецируется на эту плоскость в виде прямого угла.

Задачи

14. Определить расстояние от точки С до прямой (АВ) (рис.19).

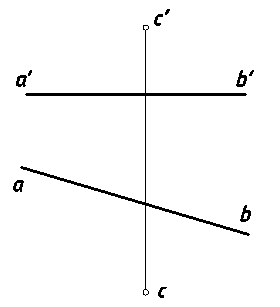
Рис. 19.

15. [СM] – высота равнобедренного Δ ABC. [СM] ║ H. Точка А принадлежит плоскости Н, точка В принадлежит плоскости V (рис. 20).

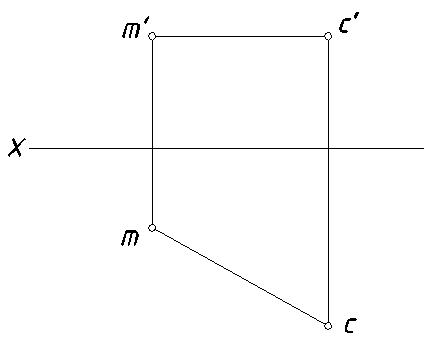
Рис. 20.

16. Найти недостающую проекцию точки С, отстоящей от отрезка [АВ] на 30 мм (рис. 21).

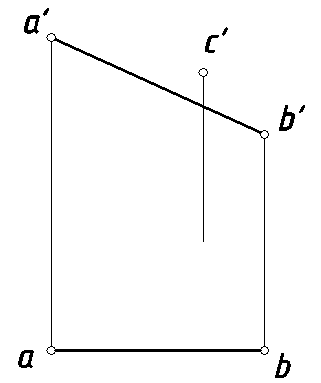
Рис. 21.