
- •Конспект лекций по информатике
- •1 Семестр Содержание
- •Тема 5 Модели решения функциональных и вычислительных задач 45
- •Тема 1 введение в информатику
- •Лекция 1 основные понятия информатики
- •Появление и развитие информатики
- •Предмет, задачи и методы информатики
- •Структура информатики
- •Тема 2 информация и информационные процессы
- •Лекция 2 информация и информационные процессы
- •Понятие информации. Развитие представлений об информации
- •Методы воспроизведения и обработки данных
- •Свойства информации
- •Основные процессы преобразования данных. Информационный обмен
- •Измерение количества информации
- •Классификация электронных вычислительных машин
- •Понятие архитектуры и структуры эвм
- •Персональные компьютеры. Типовой комплект персонального компьютера
- •Структура персонального компьютера (пк)
- •Системная (материнская плата)
- •Тема 4 программные средства реализации информационных процессов
- •Лекция 5 общая характеристика программного обеспечения
- •Основные понятия программного обеспечения
- •Постановка задачи Алгоритмизация решения задачПрограммирование
- •Категории специалистов, занятых разработкой и эксплуатацией программ
- •Характеристика программного продукта
- •Жизненный цикл программного продукта
- •Защита программных продуктов
- •Программные системы защиты от несанкционированного копирования
- •Правовые методы защиты программных продуктов и баз данных
- •Классификация программных продуктов
- •Лекция 6 системное программное обеспечение
- •Структура системного программного обеспечения
- •Понятие операционной системы и её функции
- •Состав операционной системы
- •Характеристики операционной системы
- •Классификация операционных систем
- •Операционные системы семейства Windows
- •Операционные системы семейства Unix, операционная система Linux
- •Основные тенденции развития ос
- •Сервисное системное программное обеспечение
- •Тема 5 Модели решения функциональных и вычислительных задач
- •Лекция 7 Логические основы компьютера
- •Виды логических функций (операций)
- •Лекция 8 системы счисления
- •Понятие системы счисления. Виды систем счисления.
- •Если справа - прибавляется.
- •В позиционных системах счисления основание системы равно количеству цифр (знаков в ее алфавите) и определяет, во сколько раз различаются значения одинаковых цифр, стоящих в соседних позициях числа.
- •Позиция цифры в числе называется разрядом. Разряд числа возрастает справа налево, от младших разрядов к старшим.
- •В двоичной системе счисления основание равно 2, а алфавит состоит из двух цифр (0 и 1).
- •Перевод чисел в позиционных системах счисления Правила перевода целых чисел
- •Правила перевода дробных чисел
- •Необходимо записать число в развернутой форме и вычислить его значение.
- •2.2. Перевод чисел из десятичной системы в двоичную, восьмеричную и шестнадцатеричную
- •Алгоритм перевода целого десятичного числа в двоичное будет следующим:
- •Представление информации в эвм
Тема 5 Модели решения функциональных и вычислительных задач
Лекция 7 Логические основы компьютера
План лекции:
1. Виды логических функций (операций).
2. Таблицы истинности логических функций (операций).
3. Приоритет выполнения логических функций. Примеры решения задач.
Логические системы предназначены для описания и получения правильных рассуждений, представляющих собой цепь умозаключений в логически последовательной форме.
Элементарные объекты, участвующие в рассуждениях это логические высказывания, истинность которых можно установить.
Логическим выражением называется утверждение, в отношении которого, всегда можно сказать истинно оно или ложно.
Например:
«6 – четное число» - истинное высказывание.
«Брянск – областной центр Смоленской области» – ложное высказывание.
Не являются логическими высказываниями вопросительные утверждения и высказывания типа: «Студент первого курса», «Сложный вопрос».
Определите, является ли высказыванием выражение:
«В городе N- миллион жителей»?
Значения истинно или ложь называются логическими значениями.
В разных системах они могут обозначаться по-разному:
Истина Ttrue 1
Ложь False 0
Сами логические высказывания принято обозначать буквами латинского алфавита: А, B, C и т.д.
Элементарные логические высказывания, обозначенные буквами латинского алфавита и независящие друг от друга, которые могут принимать значения истина или ложь называют логическими переменными.
Каждая логическая операция, которая производится над логическими переменными, имеет свое название и обозначение.
Операции над одной переменной называются унарными. Операции над двумя переменными называются бинарными.
Виды логических функций (операций)
• логическое сложение +, или дизъюнкция V;
• логическое умножение •, или конъюнкция &;
• отрицание (по первой переменной) a (с чертой над символом);
• отрицание (по второй переменной) b (с чертой над символом) ;
• импликация, или функция следования - левая → (с чертой над символом) и правая ← (с чертой над символом);
функция тождества, или эквивалентность ~; и др.;
Значение каждой логической функции описывается таблицей истинности.
Таблица истинности представляет собой таблицу, устанавливающую соответствие между возможными значениями наборов переменных и значениями функции.
Таблицы истинности логических функций позволяют определять значение, которые принимают эти функции при различных значениях переменных, сравнивать функции между собой, определять, удовлетворяют функции заданным свойствам.
Таблицы истинности логических функций (операций)
Логическое сложение а+b, или дизъюнкция аVb или or или v или |
Читается эта запись как "а плюс б" или "а дизъюнкция б".
Дизъюнкция двух слагаемых ложна тогда и только тогда, когда ложны оба слагаемых.
Таблица истинности логического сложения следующая:
-
а
b
а + b
0
0
0
0
1
1
1
0
1
1
1
1
Логическое умножение а • b, или конъюнкция а & b или ^ или and
•Запись читается как "а b" или "а конъюнкция b".
Конъюнкция двух сомножителей истинна тогда и только тогда, когда истинны оба сомножителя.
Таблица истинности у этой функции следующая:
а |
b |
а * b |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
Отрицание
а,
¬,
![]()
Запись читается как "не-а".
Отрицание лжи есть истина, отрицание истины, есть ложь. Таблица истинности у отрицания следующая:
а |
|
0 |
1 |
1 |
0 |
Импликация,
или функция следования: левая а
![]() b
и правая а
b
и правая а
![]() b
b
Запись а b читается как "а импликация б " или из " а следует б ", а запись а b читается как "б импликация а" или "из б следует а".
Для функции импликации из лжи следует все что угодно, a из истинности только истина.
Таблица истинности левой импликации определяется следующим образом:
а |
b |
а b |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
Для правой импликации таблица истинности такова;
А |
b |
|
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
Функция тождества, или эквивалентность а ~ b
Запись читается как "а эквивалентно б". Функция истинна тогда и только тогда, когда значения переменных совпадают.
Таблица истинности функции такова:
-
а
b
a~b
0
0
1
0
1
0
1
0
0
1
1
1
Приоритет выполнения логических операций:
Отрицание;
Логическое умножение ;
Логическое сложение;
Импликация;
Следование;
Эквивалентность.
Пример. Составить таблицу истинности для выражения: ¬(AvB)
A |
B |
¬(AvB) |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
Вопросы для самоконтроля:
Что такое «логическое высказывание» и «логическое выражение».
Что такое «таблица истинности»?
Какие логические функции вы знаете?
Как принято обозначать логические операции: сложение, умножение, отрицание, эквивалентность, следования?
Каков приоритет выполнения логических операций?
Составьте таблицу истинности для выражения: ¬С v (¬A v B) & А v В
Составьте таблицу истинности для выражения: С v ¬ (A v B) v С & ¬В
Примеры тестовых заданий:
Логические устройства ЭВМ проектируются на основе математического аппарата:
аналитической геометрии
теории графов
реляционной алгебры
булевой алгебры
Логическая операция А ^ В называется:
инверсия (логическое отрицание)
дизъюнкция (логическое сложение, "или")
импликация ("если …, то …")
конъюнкция (логическое умножение, "и")
Указанная таблица истинности соответствует операции:
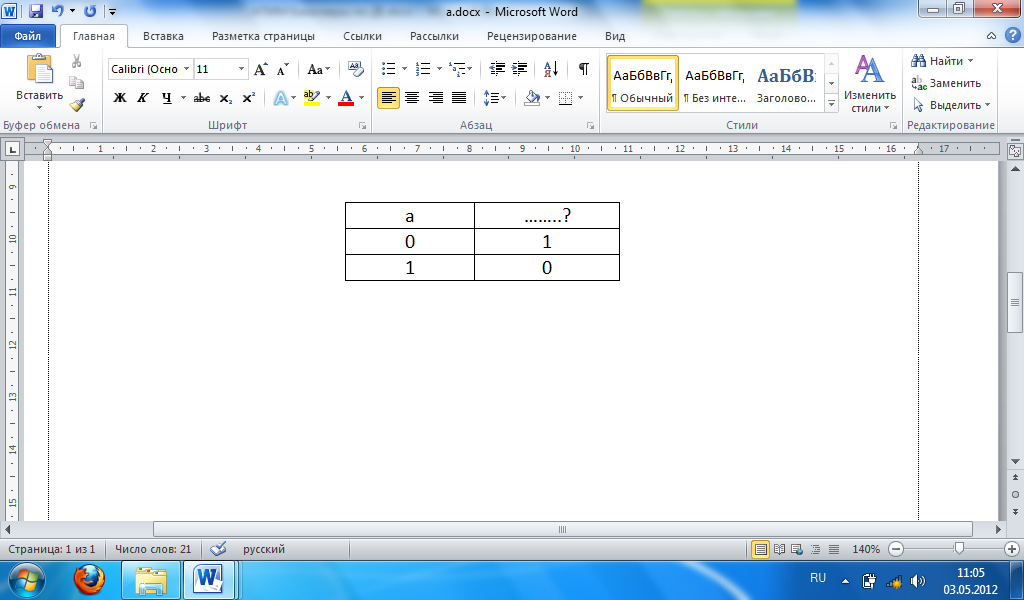
логического умножения
отрицания
эквивалентности
импликации
Указанная таблица истинности соответствует операции:
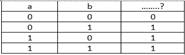
логического сложения
логического умножения
эквивалентности
импликации
Указанная таблица истинности соответствует операции:
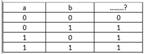
логического сложения
логического умножения
эквивалентности
импликации
