3 Расчет переходного процесса в гидромеханической системе без учета сжимаемости жидкости.

Запишем уравнение движения выходного элемента гидродвигателя для гидромотора:

, где

- угловое перемещение вала гидромотора, рад;

- приведенный момент инерции, ;

- движущий момент на валу гидромотора, ;

- момент сопротивления вала гидромотора, ;

;

Тогда уравнение примет вид

, где

Из уравнения расхода выразим и подставим в уравнение выше:

;

- момент инерции исполнительного органа, ;

- момент инерции вала гидромотора, ;

- приведенный момент инерции жидкости напорного трубопровода, ;

- приведенный момент инерции жидкости сливного трубопровода, ;

Найдем приведенный момент инерции жидкости напорного и сливного трубопроводов, используя уравнение кинетической энергии жидкости.

, где

- длины участков напорного трубопровода, ;

- площади участков напорного трубопровода, ;

- длины участков сливного трубопровода, ;

- площади участков сливного трубопровода, ;

Тогда будет равно

Подставим все значения в уравнение движения выходного элемента гидродвигателя для гидромотора:

И приведем к виду:

,

- установившееся значение скорости вала гидромотора;

, где

Таблица 2

t	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1	1,1	1,2	1,3
	0	0,57	0,85	0,96	0,98	0,99	0,99	0,99	0,99	0,99	1	1	1	1
V	0	92,2	138	154,6	159,2	160,5	160,8	160,9	160,9	160,9	161	161	161	161

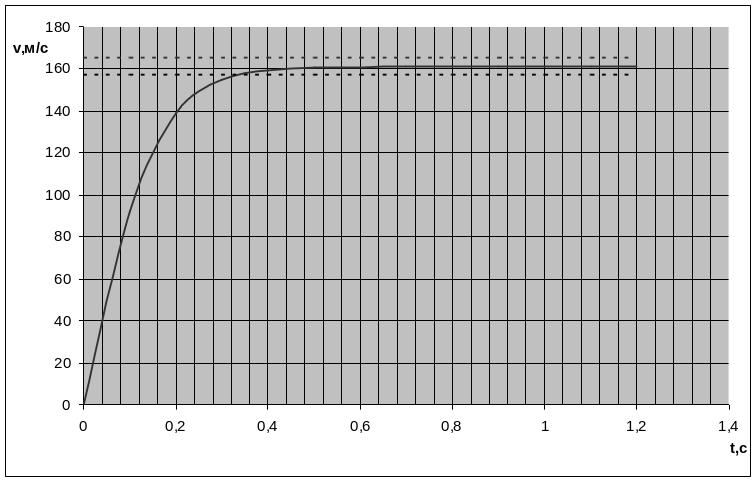
Рисунок 4- График переходного процесса в гидромеханической системе при ступенчатом изменении расхода и без учета сжимаемости жидкости.

Время переходного процесса определяем по графику (Рис. 4) – время достижения установившегося значения скорости выходного элемента гидродвигателя. На графике это время фиксируется в момент вхождения кривой в пятипроцентное отклонение от установившегося значения скорости:

4 Расчет переходного процесса в гидромеханической системе с учетом сжимаемости жидкости.

Для упрощения математической модели линеаризуется нелинейная зависимость суммарных потерь давления в напорной и сливной гидролинии от скорости выходного элемента гидродвигателя.

- приведенный суммарный коэффициент сопротивления трубопровода;

Таблица 3

Рис.4- График зависимости суммарных потерь давления от скорости выходного элемента гидродвигателя

Для линеаризации расходной характеристики определим коэффициент расхода дросселя:

Линеаризованное уравнение расходной характеристики, полученной из разложения в ряд Тейлора

Уравнение расхода с учетом сжимаемости жидкости:

, где

, ;

- суммарный объем напорного трубопровода, ;

;

- приведенный модуль упругости системы «жидкость – напорный трубопровод», Па;

, где

- средний радиус напорного трубопровода, м;

- модуль упругости материала стенки трубопровода, Па;

Па;

- толщина стенки трубопровода, м;

- коэффициент Пуассона;

- адиабатический модуль упругости жидкости, Па;

- адиабатическая скорость звука в жидкости, ;

Определим :

;

Па;

;

;

МПа;

Па;

Определим суммарный объем напорного трубопровода:

Из уравнения движения выражаем :

Запишем это выражение с учетом линеаризованных соотношений:

Определим первую производную давления по времени:

Подставим полученные выше выражения в уравнение расхода с учетом сжимаемости жидкости:

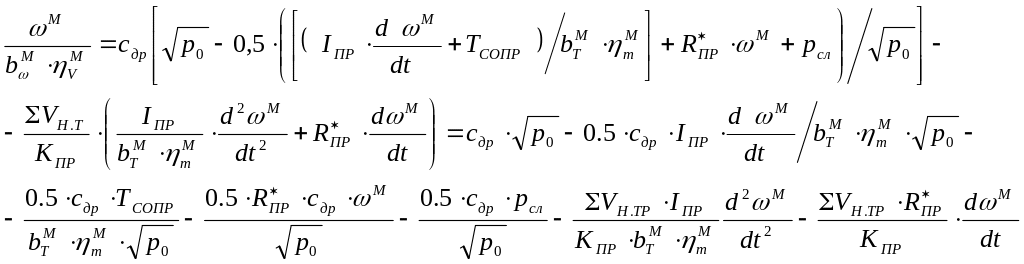
Упростим выражение выше, принимая:

Получили

И приведем к виду неоднородного дифференциального уравнения второго порядка с правой частью: (*),

где

Уравнение (*) приводим к виду: ,

где - общее решение дифф. уравнения второго порядка с правой частью;

- общее решение однородного уравнения (*); ;

- частное решение неоднородного уравнения при и , определяемое зависимостью .

.

и - сопряженные комплексные числа, поэтому

Определим коэффициенты и . Для этого продифференцируем по времени величину и используем граничные условия вида , при .

При :

;

.

Тогда:

Таблица 4

Строим график переходного процесса в гидромеханической системе при ступенчатом изменении расхода сжимаемой жидкости (рис. 5). Этот график представляет собой колебательный затухающий процесс с учетом сжимаемости рабочей жидкости и демпфированием колебаний.

Рис.5 - График переходного процесса в гидромеханической системе при ступенчатом изменении расхода сжимаемой жидкости.

Список использованных источников:

1. Свешников В.К. Станочные гидроприводы: Справочник: Библиотека конструктора. – 4-е изд. перераб. и доп. – М.: Машиностроение, 2004. – 512с.: ил.

2. Квашнин А.И. Статический и регулирование гидро- и пневмосистем. Статический расчет и расчет переходных процессов в гидромеханической системе: учеб.-метод. пособие / А.И. Квашнин. – Пермь: Изд-во Перм. гос. техн. ун-та, 2007.- 28 с.

3. Механика жидкости. Гидравлические машины и основы гидропривода агрегатов ракетных комплексов/ Ю. М. Орлов. – Министерство обороны РФ – Пермь: Пермский военный институт ракетных войск. Пермь, 2001. – 380 с

20