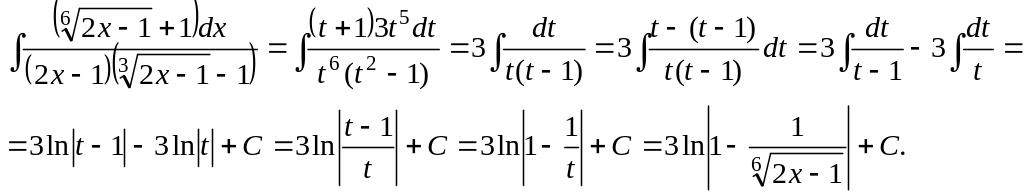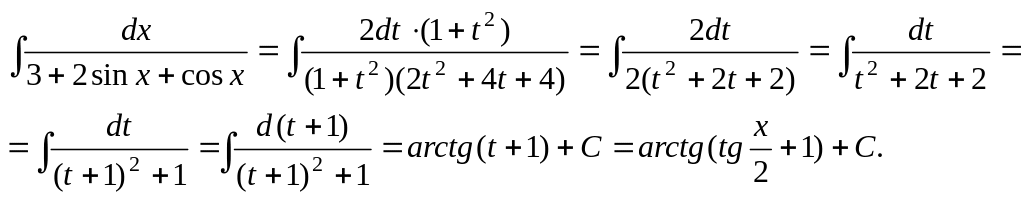8.4.3. Интегрирование некоторых видов иррациональностей

При интегрировании иррациональных функций основная задача заключается в выборе такой подстановки, которая данное подынтегральное выражение преобразует в рациональное.

Рассмотрим интеграл вида

.

Этот интеграл рационализируется с помощью подстановки .

Пример. Вычислить интеграл . Под знаком интеграла содержатся корни с разными показателями, но с одним и тем же подкоренным выражением. Наименьшее общее кратное показателей корней равно 6, поэтому используем подстановку . Отсюда . Заменяя переменную в интеграле, получим:

Рассмотренный интеграл является частным случаем интеграла

.

В этом случае подстановка сводит интеграл к интегралу от рациональной функции.

В общем случае интеграл имеет вид:

,

где — рациональные числа.

Для решения необходимо найти общий знаменатель дробей и воспользоваться подстановкой .

Пример. Вычислить интеграл . Используем подстановку , тогда Подставляя полученные выражения в исходный интеграл, получим:

8.4.4. Интегрирование тригонометрических функций

Рассмотрим интегралы вида: , где — рациональная функция от и .

Такие интегралы всегда рационализируются с помощью универсальной подстановки

Тогда .

Пример. Вычислить интеграл . Воспользуемся универсальной подстановкой , тогда получим: Заменив переменную, вычислим интеграл.

Универсальная подстановка во многих случаях приводит к громоздким выкладкам, поэтому рассмотрим некоторые частные подстановки, упрощающие вычисления.

• Подынтегральная функция является нечётной относительно , то есть В этом случае используется подстановка .

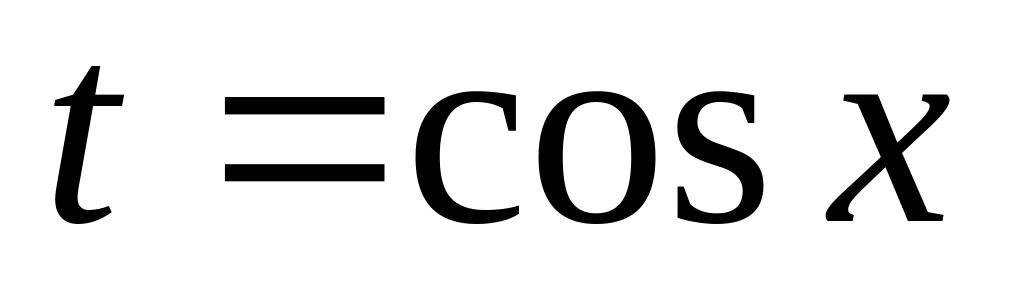• Подынтегральная функция является нечётной относительно , то есть В этом случае используется подстановка .

• Если подынтегральная функция зависит нечётным образом и от , и от , то можно использовать подстановки или или .

• Если подынтегральная функция зависит чётным образом и от , и от , тогда используем подстановку . Отсюда:

;

Пример. Вычислить интеграл . В данном случае имеем: Воспользуемся подстановкой , откуда . Тогда имеем:

8.5. Примеры вычисления неопределенных интегралов

1. Вычислить интеграл .

Интегрируем по частям:

Имеем:

Полученный интеграл ещё раз интегрируем по частям:

Окончательно получим:

2. Вычислить интеграл .

Интегрируем по частям:

.

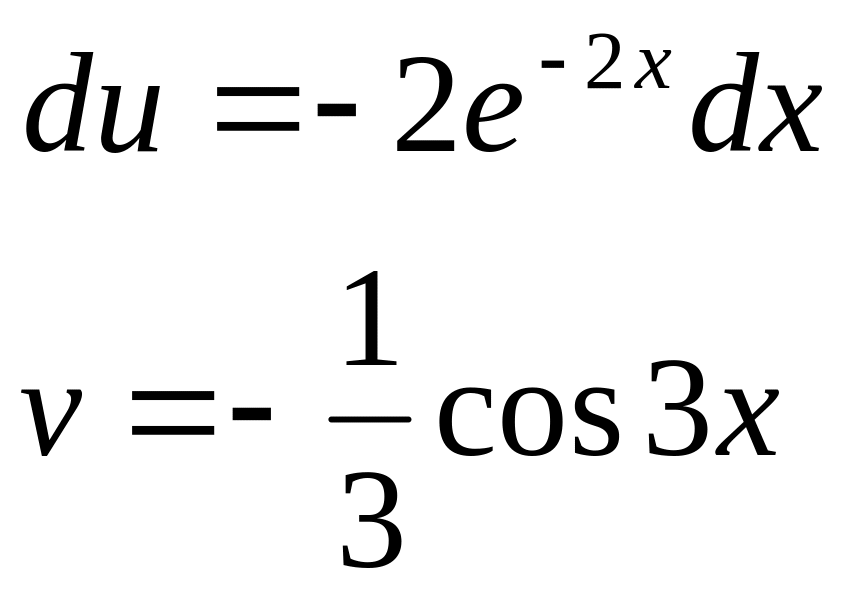Имеем:

.

Мы получили интеграл той же сложности, что и исходный. Проинтегрируем его ещё раз по частям:

,

Тогда:

.

Отсюда получим:

.

Перенесём интеграл из правой части последнего равенства в левую и найдём его как из уравнения:

Тогда окончательно:

3. Вычислить интеграл .

Сделаем подстановку , тогда . Тогда интеграл примет вид

.

При решении этой задачи можно рассуждать иначе. Введём множитель под знак дифференциала, тогда получим

.

4. Вычислить интеграл

Запишем интеграл в виде , тогда удобно сделать замену , .

Интеграл примет вид

.

5. Вычислить интеграл .

Числитель напоминает дифференциал от Кроме того, легко выражается через : , т. е. целесообразна подстановка , тогда

.

6. Вычислить интеграл .

Так как , то корни вещественные и

Разложим дробь , следовательно . Пусть тогда ; пусть , тогда .

Таким образом:

.

7. Вычислить интеграл .

После деления числителя на знаменатель, получаем частное и в остатке 3, так, что

.

Разложим дробь

, при , , при , .

Тогда

.

Значит исходный интеграл будет иметь вид

.

8. Вычислить интеграл .

Воспользуемся подстановкой:

Тогда получим

9. Вычислить интеграл .

Подынтегральная функция чётным образом зависит и от , и от , поэтому применяем подстановку .

Разделим числитель и знаменатель дроби на и введём под знак дифференциала множитель .

В итоге получим:

10. Вычислить интеграл .

Преобразуем подынтегральную функцию. Так как и , то:

.

Тогда

.

Воспользуемся этим преобразованием для вычисления исходного интеграла

.

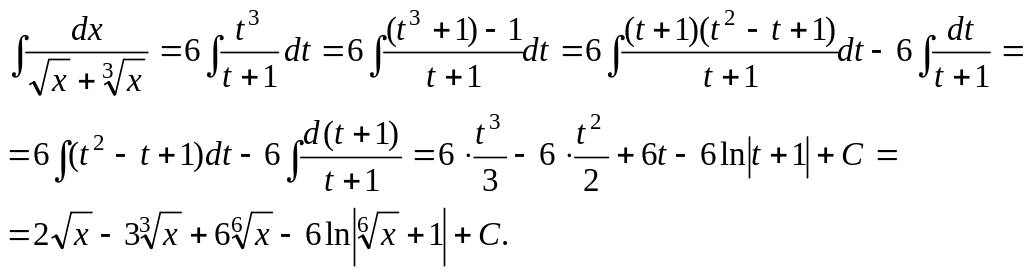
12