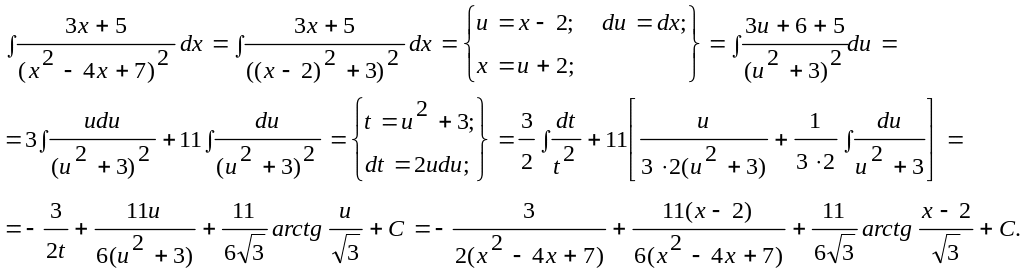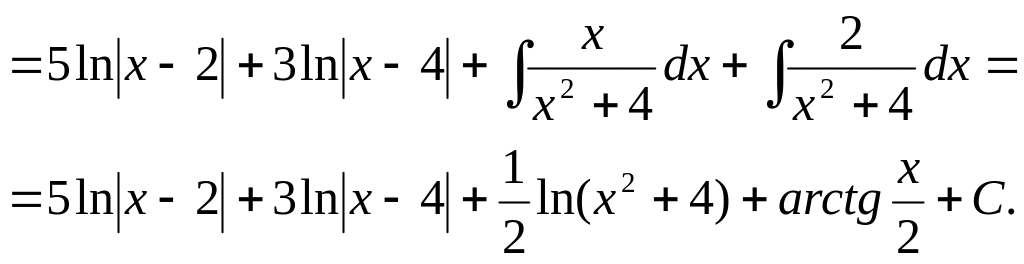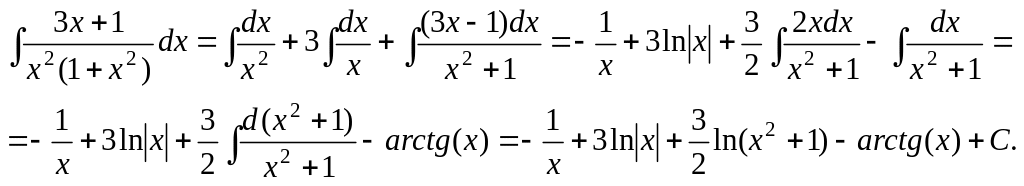8.3.3. Метод замены переменной (метод подстановки)

Метод замены переменной является одним из основных методов интегрирования. Он базируется на следующей теореме.

Теорема. Если требуется найти интеграл (но сложно отыскать первообразную), то замена x = (t) и dx = (t)dt приводит к интегралу следующего вида:

.

Пример. Вычислить интеграл . Выполним подстановку , тогда , откуда . Заданный интеграл преобразуется теперь к табличному . Возвращаясь к первоначальной переменной , получим

Замечание (частный случай). Пусть , тогда

.

Пример. Вычислить интеграл . .

Замечание. Если подынтегральное выражение содержит , то удобно применить подстановку или подстановку .

Если подынтегральное выражение содержит , то удобно применить подстановку или подстановку .

Если подынтегральное выражение содержит , то удобно применить подстановку или подстановку .

Пример. Вычислить интеграл . Так как под интегралом есть радикал , то сделаем подстановку ; откуда . Имеем: . .

8.4. Интегрирование некоторых классов функций

8.4.1. Интегрирование элементарных дробей

Определение. Элементарными называются дроби следующих четырех типов:

• 

• 

• 

• ,

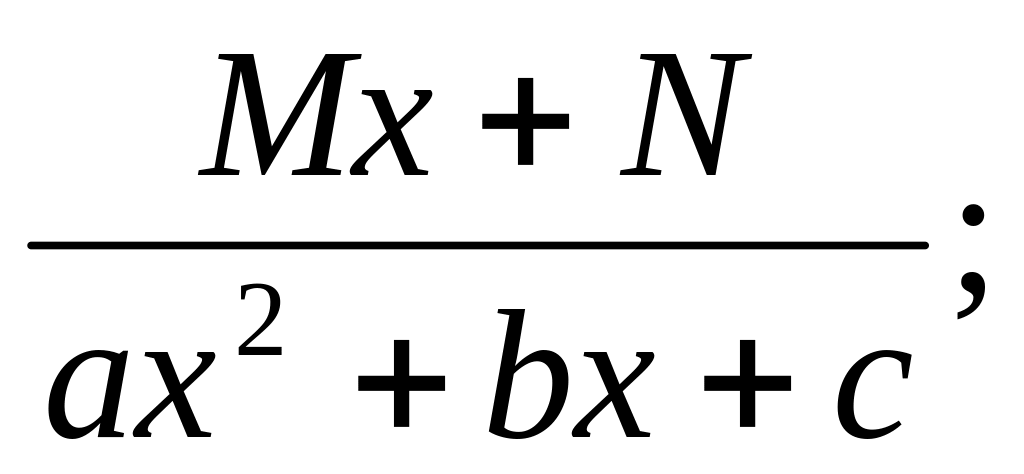
где m, n – натуральные числа (m  2, n  2) и b² – 4ac <0.

Первые два типа интегралов от элементарных дробей приводятся к табличным подстановкой вида . То есть:

Рассмотрим метод интегрирования элементарных дробей третьего вида.

Интеграл дроби третьего вида может быть представлен следующим образом:

Таким образом, интеграл третьего вида приводится к двум табличным интегралам.

Пример. Вычислить интеграл .

Для вычисления интеграла четвертого вида сначала необходимо воспользоваться следующим преобразованием:

.

После этого необходимо воспользоваться следующей заменой переменных:

В полученном равенстве первый интеграл с помощью подстановки t = u² + s приводится к табличному , а ко второму интегралу применяется рекуррентная формула:

Если применить эту формулу n-1 раз, то получится табличный интеграл .

Пример. Вычислить интеграл .

8.4.2. Интегрирование рациональных функций

Для того, чтобы проинтегрировать рациональную дробь необходимо разложить ее на элементарные дроби. Рассмотрим рациональную функцию , где — многочлен степени , — многочлен степени .

Если , то есть дробь неправильная, то её можно представить в виде , где - правильная дробь. Взятие интеграла от первого слагаемого не вызывает сложностей. Второе слагаемое - правильная дробь может быть разложена на элементарные дроби указанных выше четырех видов. Для разложения правильной дроби необходимо воспользоваться следующей теоремой.

Теорема. Если - правильная рациональная дробь, знаменатель которой представлен в виде произведения линейных и квадратичных множителей (отметим, что любой многочлен с действительными коэффициентами может быть представлен в таком виде: = (x - a)^…(x - b)^(x² + px + q)^…(x² + rx + s)^ ), то эта дробь может быть разложена на элементарные по следующей схеме:

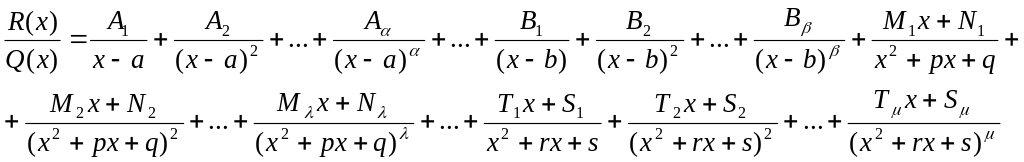
где A_i, B_i, M_i, N_i, Т_i, S_i – некоторые постоянные величины.

Для нахождения величин A_i, B_i, M_i, N_i, Т_i, S_i применяют так называемый метод неопределенных коэффициентов (суть которого состоит в том, что для того, чтобы два многочлена были тождественно равны, необходимо и достаточно, чтобы были равны коэффициенты при одинаковых степенях х).

Пример. Вычислить интеграл . Так.как знаменатель может быть разложен следующим образом: ( , то на основании теоремы правильная дробь будет записана в виде: Приводя правую часть соотношения к общему знаменателю и приравнивая числители правой и левой частей, получаем: Группируя коэффициенты при одинаковых степенях х, получаем: Приравнивая коэффициенты при одинаковых степенях х правой и левой частей соотношения,:имеем: Таким образом, после использования теоремы исходный интеграл свелся к следующим трем интегралам, которые могут быть вычислены: Пример. Вычислить интеграл . Разложим подынтегральную дробь на простейшие. . Найдём числа с помощью метода неопределённых коэффициентов. Приведём правую часть последнего равенства к общему знаменателю. . Освобождаясь от знаменателей, получим: . Приравнивая коэффициенты при одинаковых степенях в обеих частях равенства, получим систему уравнений для определения коэффициентов Таким образом, мы получили разложение рациональной дроби на простейшие . Интегрируя, получим: