8. Неопределённый интеграл

Определение. Функция называется первообразной для на некотором промежутке , если для всех

.

Теорема. Если и — первообразные для функции в , то найдется такое число , что справедливо равенство

.

Из теоремы следует, что, если — первообразная для функции , то задает все возможные первообразные для .

Определение. Множество всех первообразных для функции на промежутке называется неопределённым интегралом для и обозначается , то есть , где — произвольная постоянная.

Вычислить неопределённый интеграл — это значит найти множество всех первообразных для подынтегральной функции.

Замечание. Очевидно, что задача интегрального исчисления является обратной к задаче дифференциального исчисления.

8.1. Основные свойства неопределённого интеграла

• Дифференциал от неопределённого интеграла равен подынтегральному выражению:

• Неопределённый интеграл от производной некоторой функции равен этой функции, сложенной с некоторой произвольной постоянной:

• Постоянный множитель k можно выносить за знак неопределённого интеграла:

• Неопределённый интеграл алгебраической суммы равен алгебраической сумме интегралов слагаемых:

8.2. Таблица интегралов

Для удобства значения неопределенных интегралов большинства элементарных функций собраны в специальные таблицы интегралов, которые могут быть весьма объемными. В них включены различные наиболее часто встречающиеся комбинации функций. Ниже приводятся самые распространенные табличные интегралы.

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. 

14. 

15. 

16. .

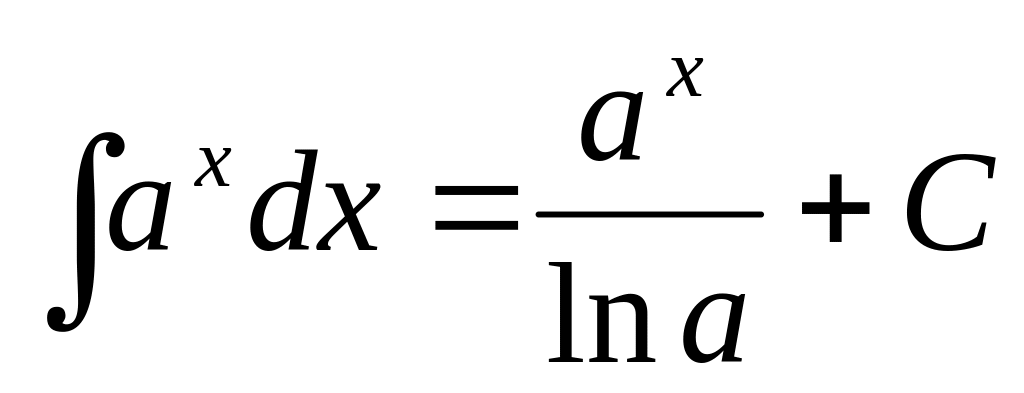
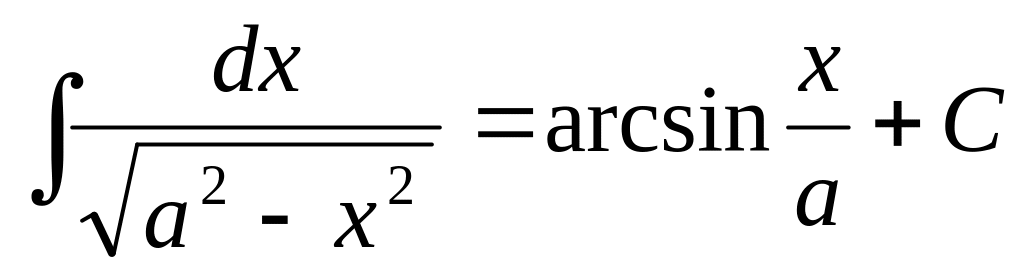
8.3. Методы интегрирования

Нахождение значения неопределенного интеграла связано главным образом с нахождением первообразной функции. Для некоторых функций это достаточно сложная задача. Ниже рассматриваются способы нахождения неопределенных интегралов для основных классов функций.

8.3.1. Метод непосредственного интегрирования

Метод непосредственного интегрирования основан на предположении о возможном значении первообразной функции с дальнейшей проверкой этого значения дифференцированием. Этот метод интегрирования опирается на таблицу основных интегралов и простейшие правила интегрирования.

Пример. Вычислить интеграл . Разделим почленно числитель подынтегральной функции на знаменатель. Применяя свойства интегралов и таблицу интегралов, получим: .

8.3.2. Метод интегрирования по частям

Метод интегрирования по частям основан на формуле

которая называется формулой интегрирования по частям.

Применяя этот метод, необходимо вначале представить подынтегральное выражение в виде произведения одной функции на дифференциал другой функции. Пользуясь указанной формулой, необходимо следить за тем, чтобы подынтегральное выражение было не сложнее, чем подынтегральное выражение .

При вычислении можно пользоваться следующими практическими советами. Если подынтегральное выражение представляет собой произведение либо тригонометрической функции на многочлен, либо показательной на многочлен, то за следует принимать этот многочлен.

Если в подынтегральное выражение входит множителем либо одна из обратных тригонометрических функций, либо функция , то за следует выбирать одну из указанных функций.

Пример. Вычислить интеграл . Положим Используя формулу интегрирования по частям, получим