
- •II. Механические свойства полимеров
- •II.1.Деформационные свойства полимеров при малых нагрузках и деформациях
- •II.1.1. Мгновенные упругие (гуковские и высокоэластические) деформации и установившееся вязкое течение аморфных полимеров.
- •II.1.2. Вязко-упругость и упруго-вязкость полимеров: процессы механической релаксациив полимерах при различных временных режимах нагружения/деформирования (феноменологическое описание)
- •II.2.1. Квазистатические режимы
- •II.2.2. Динамические режимы
- •II.1.3. Реологические состояния аморфных полимеров и релаксационные (механические реологические) переходы в них.
- •3.2. Обобщенные механические релаксационные спектры полимеров в однофазном аморфном состоянии
- •II.1.4. Возможности и примеры применения механической релаксационной спектрометрии для исследования молекулярного теплового движения и релаксационных переходов в полимерах
а) Формально-кинетическое описание
При малом удалении от равновесия любой системы, в том числе при малых нагрузках и деформациях полимеров, кинетика релаксационного процесса характеризуется скоростью уменьшения его движущей силы как меры отклонения системы от равновесного состояния, причем в случае так называемой линейной релаксации, или процесса первого порядка эта скорость пропорциональна величине движущей силы [Рел.св-ва. с, с.129,13]:
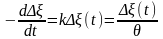 (2.1а)
(2.1а)
где Δξ(t) - движущая сила
процесса, т.е.отклонение некоторого
убывающего во времени параметра системы
ξ(t), выведенной из
равновесия, от его равновесного, или
остаточного значения ξе:
 ;
k – константа скорости
процесса, обратная величина которой
соответствует характерному времени
процесса (времени релаксации) θ.
Интегрирование уравнения (2.1а) от 0
до t дает экспоненциальную
интегральную функцию уменьшения (спада)
движущей силы во времени t
от его начального значения (при t=0)
Δξ0:
;
k – константа скорости
процесса, обратная величина которой
соответствует характерному времени
процесса (времени релаксации) θ.
Интегрирование уравнения (2.1а) от 0
до t дает экспоненциальную
интегральную функцию уменьшения (спада)
движущей силы во времени t
от его начального значения (при t=0)
Δξ0:
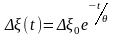 , (2.2а)
, (2.2а)
Движущей силой релаксационного процесса
в режиме релаксации нагрузки в
любой момент времени при заданной
деформации является величина нагрузки
в данный момент Р(t) за
вычетом остаточной нагрузки в условиях
равновесия P∞ (при t→∞):
ΔР=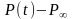 .
Cкорость релаксации
нагрузки, или уменьшения движущей силы
в этом случае описывается уравнением
(2.1а) в виде:
.
Cкорость релаксации
нагрузки, или уменьшения движущей силы
в этом случае описывается уравнением
(2.1а) в виде:
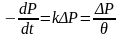 (2.1б)
(2.1б)
Интегрирование этого уравнения по времени дает интегральное выражение для релаксации нагрузки во времени:
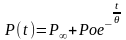 (2.2б)
(2.2б)
Движущей силой релаксационного процесса
в режиме ползучести в любой
момент времени t при
заданной нагрузке является предельное
значение деформации в условиях равновесия
R∞ (при t→∞)
за вычетом величины отклика в данный
момент времени R(t)
и мгновенного отклика R0
(при t →0): ΔR= .
При этом выражение для скорости уменьшения
движущей силы и нарастания отклика в
соответствие с уравнением (2.1а)
имеет вид:
.
При этом выражение для скорости уменьшения
движущей силы и нарастания отклика в
соответствие с уравнением (2.1а)
имеет вид:
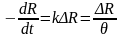 (2.1в)
(2.1в)
Интегрирование этого уравнения дает интегральное выражение для изменения деформации (ползучести) во времени:
 ) (2.2в)
) (2.2в)
Отношения Р(t)/R∞ и R(t)/P∞ называют релаксационным модулем М(t) и податливостью при ползучести J(t) соответственно. В этом случае уравнения (2.2б) и (2.2в) записываются в виде:
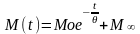 (2.3а)
(2.3а)
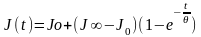 (2.3б)
(2.3б)
б) Подход механики деформирования сплошных сред
В механике сплошных конденсированных твердых и жидких сред механическое воздействие в простейшем случае характеризуется напряжением при растяжении/сжатии σ, простом сдвиге τ или объемном сжатии р и соответствующим откликом (смещением, или деформацией) ε, γ или κ, а также скоростями нагружения и деформирования (их производными по времени). В линейной механике деформирования соотношения между напряжениями и деформациями, а также между напряжениями и скоростями деформирования линейны, что соответствует, законам Гука и Ньютона для идеально упругих (твердых) и идеально вязких (жидких) сред. Коэффициенты пропорциональности в законах Гука и Ньютона (модули упругости Е, G, К или податливости J, Jl, JV и вязкости η, ηl, ηV при растяжении/сжатии, простом сдвиге и объемном сжатии соответственно) не зависят от величины напряжения, деформации и скорости деформирования при малых их значениях, т.е. в условиях малого отклонения от равновесного состояния, и связаны между собой при различных видах нагружения или деформирования через коэффициент Пуассона ν:
E=2G(1+
ν)=3K(1-2 ν);
 ; ηl=2η(1+
ν) = 3ηv(1-2
ν) (2.4)
; ηl=2η(1+
ν) = 3ηv(1-2
ν) (2.4)
Эти соотношения позволяют переходить от параметров упругости и вязкости при одном виде нагружения или деформирования к другому. В данном разделе используются преимущественно параметры напряжения, деформации, скорости деформирования, модуля упругости, податливости и вязкости при простом сдвиге (τ, γ, dγ/dt=γ∙, G, J и η соответственно). В большинстве случаев приводимые ниже феноменологические соотношения, описывающие релаксационные процессы, протекающие при сдвиге в вязко-упругих и упруго-вязких средах, сочетающих линейное упругое и вязкое поведение, с использованием этих параметров имеют аналогичный вид для соответствующих параметров при других видах нагружения или деформирования или могут быть переведены для этих параметров с помощью соотношений (2.4).
Феноменологическое описание процессов механической релаксации в линейной механике деформирования сплошных сред базируется на представлениях о линейном вязко-упругом (для твердых тел) и упруго-вязком (для жидких сред) поведении как об одновременном проявлении мгновенной и замедленной упругости, т.е., соответственно, быстрого и медленного обратимого установления предельных равновесных значений деформации, прямо пропорциональных приложенной внешней нагрузке, и вязкого течения - установившегося необратимого процесса деформирования с постоянной скоростью, пропорциональной приложенному напряжению. К вязко-упругому относится поведение сред преимущественно с упругими (мгновенными и замедленными, или высокоэластическими) деформациями при отсутствии вязкого течения, а к упруго-вязкому – преимущественно с деформациями вязкого течения и незначительным проявлением мгновенной и(или) замедленной упругости. Линейное поведение вязко-упругих и упруго-вязких сред проявляется только при малых по величине напряжениях, деформациях и скоростях деформирования. Нелинейное поведение таких сред, проявляющееся при больших напряжениях, деформациях и скоростях деформирования, т.е. в условиях, далеких от равновесия (нелинейная вязко-упругость, упруго-пластичность, турбулентность) в данном разделе не рассматривается.
Обобщенное феноменологическое описание линейного вязко-упругого и упруго-вязкого поведения в механике сплошных сред носит название теории линейной вязко-упругости, в основе которой лежит принцип суперпозиции (наложения) Больцмана, постулирующий независимость и суммируемость (аддитивность) всех воздействий (напряжений) и откликов (деформаций) с учетом разности их хода во времени при линейном соотношении между напряжениями и деформациями и их скоростями и независимости коэффициентов пропорциональности в этих соотношениях от величины напряжений, деформаций и скоростей деформирования []. В соответствии с теорией линейной вязко-упругости в квазистатическом режиме релаксации нагрузки после мгновенного изменения деформации на заданную величину γ уравновешивающее напряжение τ является убывающей функцией времени τ(t). Отношение τ(t)/γ называется релаксационным модулем G(t), который также является убывающей функцией времени. В квазистатическом режиме задержки отклика (релаксации деформации, или ползучести) при действии постоянного напряжения τ деформация является возрастающей функцией времени γ(t), также как и ее отношение к τ, называемое податливостью при ползучести J(t). При этом функции τ(t), G(t), γ(t) и J(t) не зависят от величины задаваемой деформации или напряжения соответственно.
При последовательной серии деформаций γ0,γ1, …, γi, …, γn-1, γn в моменты времени t΄0=0, t΄1,…,t΄i,…,t΄n-1, t΄n в режиме релаксации напряжения, напряжение, создаваемое каждой из этих последовательных деформаций, в соответствие с принципом суперпозиции Больцмана суммируется во времени следующим образом [Тоб. с.112]:
 ,
(2.5а)
,
(2.5а)
где τ(t) – напряжение в заданный момент времени t›t’; Gr(Δt) – релаксационный модуль, ядро или функция релаксации напряжения в момент времени t-t’i=Δti; Δγi=γi-γi-1.
Для непрерывного процесса деформирования уравнение (2.5а) записывается в интегральной форме:
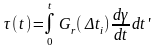 , (2.5б)
, (2.5б)
где t – заданное время (постоянное при интегрировании); t΄ – текущее время деформирования, отсчитываемое от момента задачи начальной деформации.
Аналогично, в режиме ползучести при последовательном воздействии напряжений τ0, τ1,…, τi,…τn-1, τn в моменты времени t΄0=0, t΄1,…,t΄i,…,t΄n-1, t΄n деформации, создаваемые каждым из этих последовательных напряжений, суммируются во времени в соответствие с принципом суперпозиции Больцмана следующим образом [Тоб. с.112]:
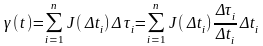 ,
(2.6а)
,
(2.6а)
где γ(t) - деформация в заданный момент времени t›t΄; J(Δti) – податливость при ползучести (ядро или функция ползучести) в момент времени t-t΄i=Δti; Δτi=τi-τi-1.
Для непрерывного процесса нагружения уравнение (2.6а) записывается в интегральной форме:
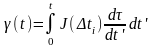 , (2.6б)
, (2.6б)
где t – заданное время (постоянное при интегрировании); t΄ – текущее время нагружения, отсчитываемое от начального момента приложения нагрузки.
Уравнения (2.5б) и (2.6б), являющиеся однозначными следствиями друг друга, в теории линейной вязко-упругости называют интегралами Больцмана-Вольтерра, т.к. они выведены из принципа суперпозиции Больцмана, а теорию таких интегралов разработал Вольтерра. Выбор функций, или ядер релаксации напряжения и ползучести в этих интегралах является произвольным с единственным условием, что функция Gr(Δti)является убывающей, J(Δti) – возрастающей. Исходя из формальных представлений кинетики релаксационных процессов первого порядка такими функциями применительно к линейным вязко-упругим и упруго-вязким средам при квазистатических режимах нагружения могут служить экспоненциальные функции (1.2б) и (1.3б) соответственно. Функции Gr(Δti) и J(Δti) могут быть выбраны в более сложной форме, исходя из формальной кинетики процессов n-го порядка, например, в виде степенных функций с несколькими константами скоростей [Фр.с.208, Аск.с.112].
в) Механическое моделирование линейного вязко-упругого и упруго-вязкого поведения
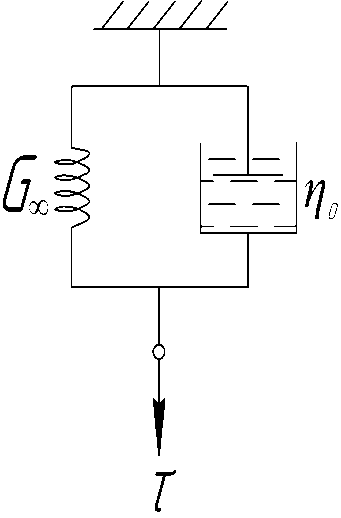
Использование механических моделей является наиболее простым и наглядным методом обобщенного феноменологического описания процессов механической релаксации в упруго-вязких и вязко-упругих средах, в том числе определения функций релаксации напряжения и ползучести. Эти модели представляют собой сочетание упругих пружин, подчиняющихся при нагружении закону Гука для мгновенных упругих деформаций, и поршней в цилиндрах с вязкой жидкостью (демпферов), поведение которых под нагрузкой подчиняется закону течения Ньютона. Последовательное и параллельное соединение таких элементов дает простейшие модели линейного вязко-упругого и упруго-вязкого поведения – модели Максвелла и Кельвина-Фойгта соответственно (Рис.2.1):

(а) (б)
Рис.2.1. Модели Максвелла (а) и Кельвина-Фойгта (б) линейных вязко-упругих и упруго-вязких сред.
Модель Максвелла характеризует линейное упруго-вязкое поведение среды без замедленной упругости, а модель Кельвина-Фойгта – наоборот вязко-упругое поведение с замедленной упругостью без течения и мгновенной упругости. Реологические уравнения состояния этих моделей, описывающие соотношения между напряжениями, деформациями и скоростями их изменения, имеют вид соответственно:
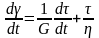 (2.7)
(2.7)
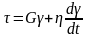 (2.8)
(2.8)
Решение этих уравнений для заданных временных условий нагружения или деформирования в квазистатических режимах дают соотношения для временных зависимостей параметров механической релаксации, в том числе функций релаксации напряжения и ползучести, аналогичных полученным из формально-кинетического описания линейной релаксации. Реологическое уравнение состояния модели Максвелла решается только для режима релаксации напряжения и дает (в терминах напряжения и деформации сдвига, т.е. при М=G) выражение для функции релаксации, аналогичное выражению (2.3а):
 , (2.9)
, (2.9)
где
 - время релаксации напряжения.
- время релаксации напряжения.
Уравнение состояния модели Кельвина-Фойгта, наоборот, решается только для режима ползучести и дает выражение для функции ползучести, аналогичное выражению (2.3 б) при J0=0:
 ), (2.10)
), (2.10)
где
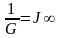 - предельная податливость,
- время запаздывания деформации.
- предельная податливость,
- время запаздывания деформации.
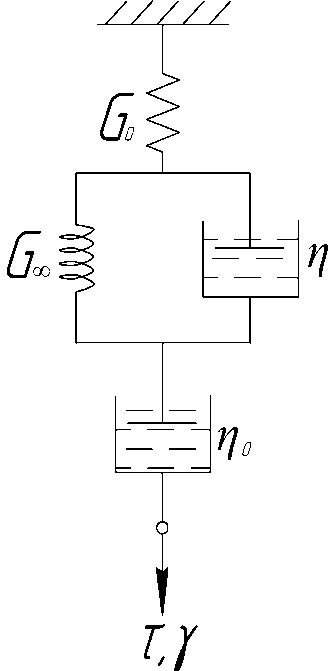
Для более полного описания поведения линейных вязко-упругих и упруго-вязких сред, в том числе применительно к полимерам и полимерным композициям, используются более сложные механические модели, представляющие собой различные комбинации последовательного и параллельного сочетания упругих и вязких элементов. Важнейшими из них являются трехэлементная модель стандартного вязко-упругого тела без необратимой текучести и четырехэлементная модель стандартного упруго-вязкого тела с необратимой текучестью (Рис.2.2а,б соответственно):

(а) (б)
Рис.2.2. Трех (а) и четырех (б) элементные механические модели вязко-упругого и упруго-вязкого тела
Трехэлементная модель (Рис.2.2а) представляет собой сочетание модели Максвелла и параллельно соединенной с ней мягкой упругой пружины с равновесными модулем упругости G∞‹‹G. Решение реологического уравнения состояния этой модели в квазистатическом режиме для релаксации напряжения дает функцию релаксации с начальным напряжением, пропорциональным G0, или начальным модулем, равным G0, и с остаточным напряжением, пропорциональным G∞, или остаточным модулем, равным G∞, при одном времени релаксации [Тоб.с.118,123]:
 , (2.11)
, (2.11)
а для ползучести - функцию ползучести с мгновенной податливостью J0=1/G0, предельной податливостью J∞=1/G∞, полностью обратимой деформацией и одним временем задержки деформации, практически равным времени релаксации напряжения:
 ,
(2.12)
,
(2.12)
где
 - время релаксации напряжения и задержки
деформации. Так как G∞‹‹G0,
то
- время релаксации напряжения и задержки
деформации. Так как G∞‹‹G0,
то
 ,
т.е. в этой модели проявляется
однокомпонентное время релаксации..
,
т.е. в этой модели проявляется
однокомпонентное время релаксации..
Приведенные на Рис.2.3 схематические изображения функций (2.11) и (2.12) в логарифмических координатах показывают, что наиболее резкое изменение этих функций наблюдается в пределах одного десятичного порядка вблизи отношения t/θ=1:
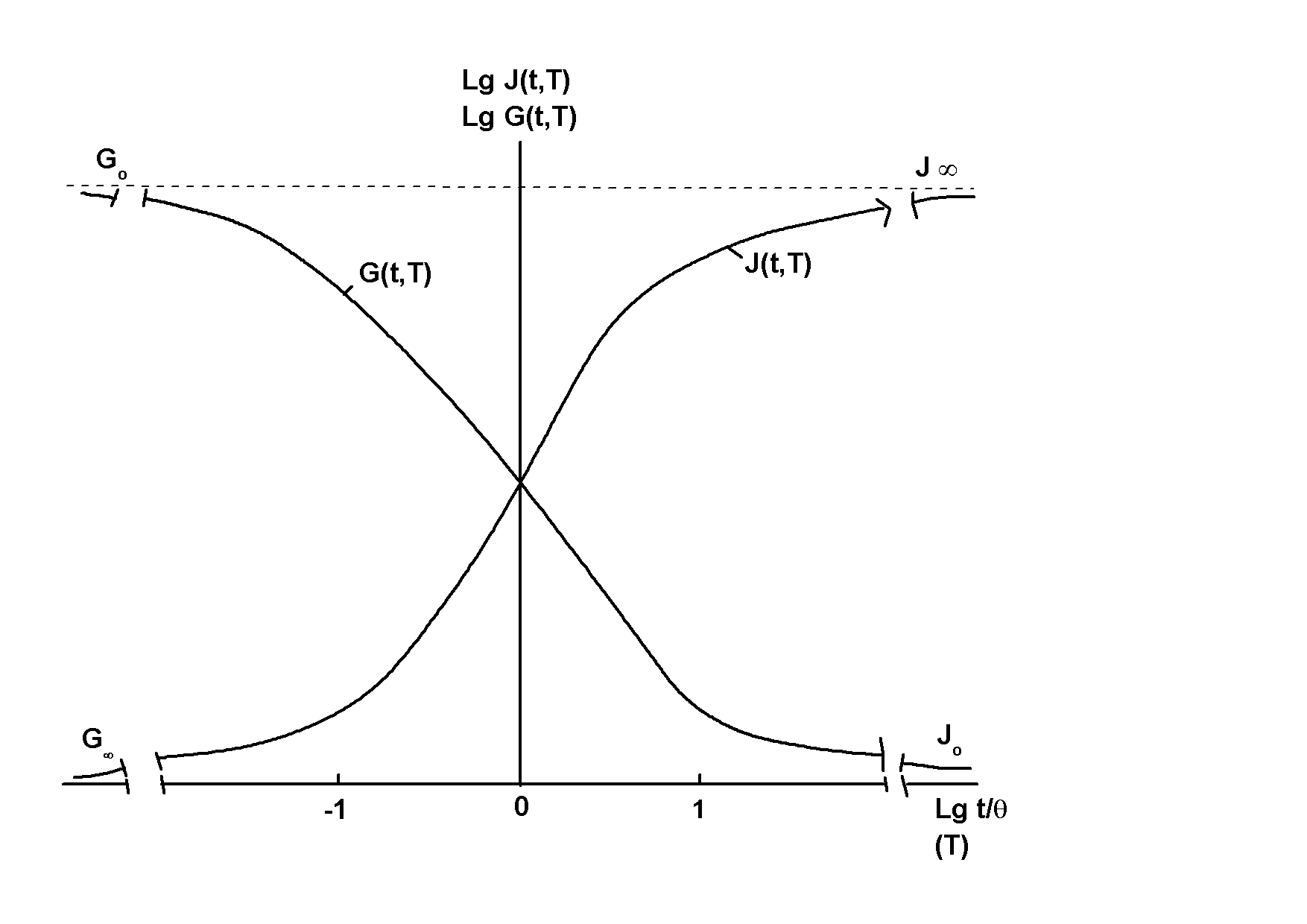
Рис.2.3. Схематическое изображение функций G(t) и J(t) для модели стандартного вязко-упругого тела без остаточных деформаций в логарифмической шкале времени (lgt/θ): при t››θ G(t)→ G∞, J(t)→ J∞, при t‹‹θ G(t) → G0, J(t) → J0.
При этом в указанном интервале соотношений t/θ для вязко-упругой модели (среды) наблюдается переход от преимущественно мгновенно упругих к преимущественно замедленным упругим деформациям, т.е. переход из одного реологического состояния в другое. С точки зрения кинетики релаксационного процесса этот переход соответствует переходу от бесконечно большого (по отношению к времени нагружения) времени релаксации (t‹‹θ) к бесконечно малому времени релаксации по отношению к времени нагружения (t››θ), т.е. переходу из одного релаксационного (реологического) состояния в другое, или релаксационному, реологическому, или кинетическому переходу. Так как в этом случае проявляется только одно время релаксации, то в узком интервале изменений соотношения t/θ возможен только один реологический переход: от преимущественно мгновенно упругих к преимущественно замедленным упругим деформациям.
Четырехэлементная модель (Рис.2.2б) представляет собой последовательное соединении элементов Максвелла и Кельвина-Фойгта, т.е. в дополнение к трехэлементной модели содержит последовательно соединенный вязкий элемент, что проявляется в наличии двух компонентов времени релаксации напряжения, обусловленных замедленной упругостью и вязким течением соответственно, и в отсутствии остаточного напряжения или модуля G∞ в функции релаксации, получаемой при решении реологического уравнения состояния этой модели:
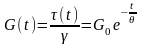 ,
(2.13)
,
(2.13)
В функции ползучести для этой модели, помимо двух компонентов времени задержки, обусловленных замедленной упругостью и вязким течением соответственно, при наличии мгновенной (J0=1/G0) и предельной (J∞=1/G∞) податливостей содержится член, учитывающий необратимую деформацию течения вязкого элемента (t/η0):
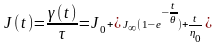 , (2.14)
, (2.14)
где
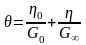 время релаксации напряжения и задержки
деформации. Хотя и в этой модели G∞‹‹G0,
но в этом случае макроскопическая
вязкость η0 намного больше
внутренней (сегментальной) вязкости η,
поэтому время релаксации является
двухкомпонентным. Соответственно, в
4-х элементной упруго-вязкой модели, в
которой проявляется два компонента
времени релаксации, в отличие от 3-х
элементной, где проявляется только одно
время релаксации, обусловленное
замедленной упругостью, в достаточно
узких интервалах изменений соотношений
t/θ возможны
два релаксационных, реологических или
кинетических перехода: от преимущественно
мгновенно упругих к преимущественно
замедленным упругим деформациям и от
преимущественно замедленных упругих
деформации к деформациям вязкого
течения.
время релаксации напряжения и задержки
деформации. Хотя и в этой модели G∞‹‹G0,
но в этом случае макроскопическая
вязкость η0 намного больше
внутренней (сегментальной) вязкости η,
поэтому время релаксации является
двухкомпонентным. Соответственно, в
4-х элементной упруго-вязкой модели, в
которой проявляется два компонента
времени релаксации, в отличие от 3-х
элементной, где проявляется только одно
время релаксации, обусловленное
замедленной упругостью, в достаточно
узких интервалах изменений соотношений
t/θ возможны
два релаксационных, реологических или
кинетических перехода: от преимущественно
мгновенно упругих к преимущественно
замедленным упругим деформациям и от
преимущественно замедленных упругих
деформации к деформациям вязкого
течения.
Комбинации бесконечно большого числа параллельно соединенных элементов Максвелла c одной мягкой упругой пружиной с равновесным модулем G∞ и последовательно соединенных элементов Кельвина-Фойгта с одной жесткой пружиной с мгновенной податливостью J0 и одним демпфером с вязкостью ηο позволяют получить, соответственно, уравнения типа (2.11) и (2.12) с дискретным набором (спектром) времен релаксации, соответствующих набору процессов механической релаксации [Тоб.]:
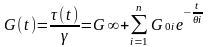 , (2.15)
, (2.15)
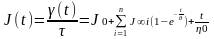 , (2.16)
, (2.16)
где G0i , J∞i – мгновенный модуль упругости и равновесная податливость i-х элементов Максвелла и Кельвина-Фойгта в обобщенных моделях соответственно.
Уравнения (2.15) и (2.16) записывают в интегральной форме, задавая для полного набора значений времен релаксации напряжения и запаздывания деформации, лежащих в интервале от 0 до ∞, непрерывные (нормированные) функции распределения F(θ) и Φ(θ) соответственно:
 , (2.17)
, (2.17)
 (2.18)
(2.18)
Уравнения (2.15) и (2.16) тождественны уравнениям Больцмана (2.5а) и (2.6а), а уравнения (2.17) и (2.18) - интегралам Больцмана-Вольтерра в теории линейной вязко-упругости соответственно [Тоб.с.120].
В обобщенной модели Максвелла при G∞=0 в режиме ползучести важный вклад в деформацию дает необратимое течение, и ее упруго-вязкое поведение может быть выражено через вязкость как функцию времени при дискретном и непрерывном спектре времен релаксации:
 (1.19)
(1.19)
Функции распределения времен релаксации и задержки F(θ) и Φ(θ) являются обобщенными характеристиками вязко-упругости и упруго-вязкости среды и представляют собой набор точек с аргументом θk и ординатами Gk и Jk, причем произведения F(θ)dθ и Φ(θ)dθ имеют размерность модуля и податливости соответственно. Хотя интегрирование функций F(θ) и Φ(θ) в уравнениях (2.17) и (2.18) производится по всему набору времен релаксации и задержки от 0 до ∞, на практике их значения могут исчезать при значениях θ, меньших некоторых минимальных (θmin) и больших некоторых максимальных (θmax) значений. Известные функции F(θ) и Φ(θ) позволяют предсказывать линейное вязко-упругое и упруго-вязкое поведение реальных систем в любых квазистатических режимах нагружения или деформирования. Определяют эти функции по известным кривым G(t) или J(t) с использованием преобразований Лапласа в интервалах θ от θmin до θmax. В свою очередь, кривые G(t) и J(t) в широком интервале t можно получить по экспериментальным данным для сравнительно узкого интервала t в широком интервале температур с использованием принципа температурно-временной аналогии и построением так называемых «обобщенных» кривых релаксации напряжения или ползучести. При построении таких кривых в логарифмической шкале времени уравнения (2.17) и (2.18) записываются с использованием логарифмических функций распределения времен релаксации H(θ) и задержки L(θ):
 ,
(2.20)
,
(2.20)
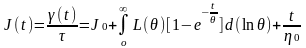 , (2.21)
, (2.21)
При этом H(θ)=θF(θ)
и L(θ)=θΦ(θ).
Для приближенной оценки функций
F(θ),Φ(θ),H(θ)
и L(θ) по
кривым G(t)
и J(t)
экспоненциальные функции в подинтегральных
выражениях (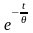 и 1-
)
уравнений (2.20) и (2.21) заменяют на ступенчатую
функцию, равную единице при t≤θ
и нулю при t≥θ. Тогда
функции F(θ),Φ(θ),H(θ)
и L(θ)
определяют, соответственно, по наклону
кривых G(t),
G(lnt), J(t) и J(lnt) в точке, в которой t=θ
[Тоб.с.126]:
и 1-
)
уравнений (2.20) и (2.21) заменяют на ступенчатую
функцию, равную единице при t≤θ
и нулю при t≥θ. Тогда
функции F(θ),Φ(θ),H(θ)
и L(θ)
определяют, соответственно, по наклону
кривых G(t),
G(lnt), J(t) и J(lnt) в точке, в которой t=θ
[Тоб.с.126]:
 ;
;
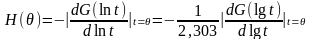 (2.22)
(2.22)
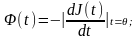
 (2.23).
(2.23).
II.2.2. Динамические режимы
К динамическим механическим режимам нагружения и деформирования относятся, в первую очередь, циклические режимы: малоамплитудные вынужденные гармонические колебания, циклы нагружения и разгрузки с заданной скоростью приложения и снятия нагрузки, а также свободно-затухающие колебания и распространение затухающих упругих колебаний и волн. Поведение вязко-упругих и упруго-вязких сред при таких режимах, аналогично квазистатическим, феноменологически описываются теорией линейной вязко-упругости, базирующейся на принципе суперпозиции Больцмана, а также решением реологических уравнений состояния линейных вязко-упругих и упруго-вязких механических моделей. В данном разделе эти подходы и методы обобщены применительно к основным типам динамических механических режимов, причем основное внимание уделено вынужденным гармоническим колебаниям, параметры которых связаны простыми соотношениями с соответствующими параметрами вязко-упругого и упруго-вязкого поведения при других динамических режимах.
а) Вынужденные гармонические колебания.
При динамических условиях нагружения и деформирования в режиме вынужденных гармонических колебаний процессы механической релаксации в вязко-упругих и упруго-вязких средах проявляются в отставании по фазе периодической деформации от прикладываемого напряжения и в опережении по фазе периодическим напряжением задаваемой деформации с обратимым накоплением упругой энергии деформирования и необратимым рассеянием ее части в виде тепла (диссипацией энергии, или механическими потерями) в каждом цикле колебаний. Взаимосвязи между периодическим напряжением и деформацией описываются в терминах комплексных чисел, что облегчает математические выкладки [Малк.с.72]. Как и в предыдущем разделе здесь основные соотношения даются в параметрах сдвига, связи которых с параметрами других видов нагружения и деформирования даны в соотношениях (2.4).
Если в вязко-упругой или упруго-вязкой
среде задается периодическая деформация,
изменяющаяся по гармоническому закону
косинуса или синуса
 ,
где γ0 – амплитудное значение
деформации, ω - круговая частота, связанная
с периодической частотой соотношением
ω=2πν, то реакцией среды является
возникновение переменного напряжения,
опережающего по фазе задаваемую
деформацию. При этом переменное
напряжение разлагается на два компонента
– совпадающий по фазе с изменением
деформации и опережающий ее на угол δ:
,
где γ0 – амплитудное значение
деформации, ω - круговая частота, связанная
с периодической частотой соотношением
ω=2πν, то реакцией среды является
возникновение переменного напряжения,
опережающего по фазе задаваемую
деформацию. При этом переменное
напряжение разлагается на два компонента
– совпадающий по фазе с изменением
деформации и опережающий ее на угол δ:
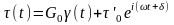 , (2.24)
, (2.24)
где G0 - мгновенный
модуль упругости; τ΄0 - амплитудное
значение компонента напряжения,
опережающего о фазе деформации на угол
δ. В качестве основных параметров
вязко-упругости при этом используются
реальный (G΄) и мнимый
(G΄΄) компоненты комплексного
динамического модуля G*,
а также отношение ,
не зависящие от амплитудных значений
τ и γ и являющиеся (в изобарно-изотермических
условиях и при соблюдении условий
линейной вязко-упругости) функцией
частоты:
,
не зависящие от амплитудных значений
τ и γ и являющиеся (в изобарно-изотермических
условиях и при соблюдении условий
линейной вязко-упругости) функцией
частоты:
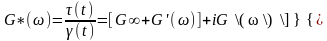 , (2.25)
, (2.25)
где G∞ - равновесный
(остаточный) модуль упругости, не
зависящий от частоты. При переходе к
тригонометрическим функциям: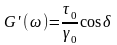 ,
,
 .
Абсолютное значение комплексного модуля
при этом равно:
.
Абсолютное значение комплексного модуля
при этом равно:
 (2.26)
(2.26)
Если к вязко-упругой и упруго-вязкой
среде по гармоническому закону
прикладывается напряжение
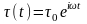 ,
где τ0 – его амплитудное значение,
то развиваемая переменная деформация
складывается из трех компонентов:
,
где τ0 – его амплитудное значение,
то развиваемая переменная деформация
складывается из трех компонентов:
а) мгновенной деформации γ0,
совпадающей по фазе с напряжением и
равной произведению J0
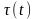 ,
где J0 - мгновенная
податливость;
,
где J0 - мгновенная
податливость;
б) деформации, запаздывающей по
отношению к напряжению на угол δ и
равной
 ,
где γ΄0 – амплитудное значение
этой деформации;
,
где γ΄0 – амплитудное значение
этой деформации;
в) деформации вязкого ньютоновского
течения, противоположной по фазе
напряжению и равной
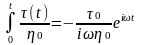 ,
где η0 – коэффициент начальной
вязкости.
,
где η0 – коэффициент начальной
вязкости.
Алгебраическая сумма этих компонентов дает выражение для периодической деформации:
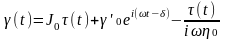 (2.27)
(2.27)
Для обобщенного описания динамического
поведения вязко-упругой и упруго-вязкой
сред при этом используется реальный
(J’) и мнимый (J”)
компоненты комплексной динамической
податливости J* а также
отношение ,
также как в случае приложения переменной
деформации не зависящие от амплитудных
значений τ и γ и являющиеся (в
изобарно-изотермических условиях и при
соблюдении условий линейной вязко-упругости)
функцией частоты:
,
также как в случае приложения переменной
деформации не зависящие от амплитудных
значений τ и γ и являющиеся (в
изобарно-изотермических условиях и при
соблюдении условий линейной вязко-упругости)
функцией частоты:
 (2.28)
(2.28)
При переходе к тригонометрическим
функциям:
 ,
,
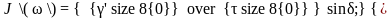
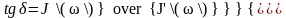 .
Очевидно, что
.
Очевидно, что
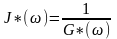 ,
однако J΄(ω)≠
,
однако J΄(ω)≠ и J΄΄(ω)≠
и J΄΄(ω)≠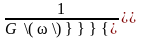 .
Если при заданной частоте J0‹‹J΄,
G∞‹‹G΄ и
.
Если при заданной частоте J0‹‹J΄,
G∞‹‹G΄ и
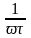 ‹‹J
, то для этой частоты получаются следующие
соотношения между компонентами
комплексной податливости и комплексного
модуля:
‹‹J
, то для этой частоты получаются следующие
соотношения между компонентами
комплексной податливости и комплексного
модуля:
 ;
;  (2.29)
(2.29)
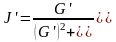

При приложении по гармоническому закону напряжения к резко выраженной упруго-вязкой среде в качестве обобщенной характеристики ее упруго-вязких свойств удобнее использовать комплексную вязкость η* и ее реальный и мнимый компоненты как функции частоты, связанные между собой соотношением:
 , (2.30)
, (2.30)
где η΄(ω)= sinδ
- параметр динамической упругости;
η΄΄(ω)=
cosδ
и
sinδ
- параметр динамической упругости;
η΄΄(ω)=
cosδ
и
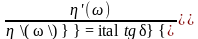 – параметры динамической вязкости и
механических потерь соответственно.
– параметры динамической вязкости и
механических потерь соответственно.
Компоненты комплексной вязкости связаны с компонентами комплексного модуля простыми соотношениями:
η’(ω)= ;
η”(ω)=
;
η”(ω)= (2.31)
(2.31)
Таким образом, определяемые в динамических режимах реальные компоненты комплексного динамического модуля и податливости, а также мнимый компонент комплексной динамической вязкости характеризуют линейные соотношения между совпадающими по фазе компонентами напряжения и деформации, т.е. упругие свойства вязко-упругих и упруго-вязких сред, и определяют величину обратимо накапливаемой и превращаемой в работу упругой энергии, равной для единицы объема за один цикл колебаний:
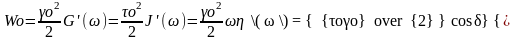 (2.32)
(2.32)
Мнимые компоненты комплексного динамического модуля и податливости, а также реальный компонент комплексной динамической вязкости характеризуют линейные соотношения между несовпадающими по фазе компонентами напряжения и деформации, т.е. вязко-текучесть вязко-упругих и упруго-вязких сред, и определяют величину необратимо рассеиваемой энергии, равной для единицы объема за один цикл колебаний:
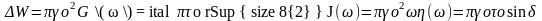 , (2.33)
, (2.33)
где γ0 и τ0 - амплитудные
значения периодических напряжений и
деформаций соответственно. Отношение
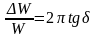 .
.
Так как компоненты комплексного динамического модуля, податливости и вязкости связаны между собой, далее их частотные зависимости и другие соотношения даются только для компонентов комплексного динамического модуля.
Функции G΄(ω) и G΄΄(ω) могут быть получены в теории линейной вязко-упругости Фурье-преобразованием соотношений Больцмана-Вольтерра для квазистатических режимов (уравнения 2.5-2.6). Фурье-преобразования позволяют при этом получать соотношения, связывающие комплексные динамические модули, податливости, коэффициент вязкости и их компоненты как функции частоты с соответствующими квазистатическими параметрами как функциями времени. Так, функция G*(ω)) связана с функцией G(t) соотношением:
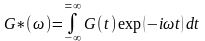 (2.33а)
(2.33а)
Связь функций G΄(ω) и G΄΄(ω) с G(t) через синус- и косинус-преобразования Фурье:
 (2.33б)
(2.33б)
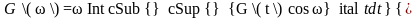 , (2.34в)
, (2.34в)
что позволяет рассчитывать динамические вязко-упругие функции по известным квазистатическим. Обратное преобразование Фурье дает функции, связывающие G(t) с G*(ω), G΄(ω) и G΄΄(ω):
 (2.35а)
(2.35а)
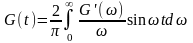 (2.35б)
(2.35б)
 (2.36)
(2.36)
Учет времени релаксации в функциях G΄(ω) и G΄(ω) наиболее просто осуществляется решением реологических уравнений состояния линейных вязко-упругих или упруго-вязких моделей для периодически прикладываемого напряжения или деформации. Так, для трех элементной модели стандартного вязко-упругого тела (см. Рис.2.2) при отсутствии вязкого течения и при одном времени релаксации θ эти функции имеют вид:
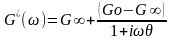 (2.37а)
(2.37а)
 ; (2.37б)
; (2.37б)
 ; (2.38)
; (2.38)
 (при G∞=0
(при G∞=0
 ), (2.39)
), (2.39)
где
 .
.
Вид этих функций, схематически изображенных на Рис.2.4 в логарифмической шкале, показывает, что наиболее резко частотные зависимости G΄(ω), G΄΄(ω) и tgδ проявляются в пределах одного десятичного порядка вблизи произведения ωθ=1, где функция G΄(ω) претерпевает перегиб. При ω→0 она стремится к G∞, а при ω→∞ - к G0 , т.е. в области частот или времен релаксации, в которой произведение ωθ→1, вязко-упругие модели, по аналогии с квазистатическими условиями нагружения и деформирования, претерпевают релаксационный переход из одного реологического состояния в другое (от преимущественно мгновенно упругих к преимущественно замедленным упругим деформациям).
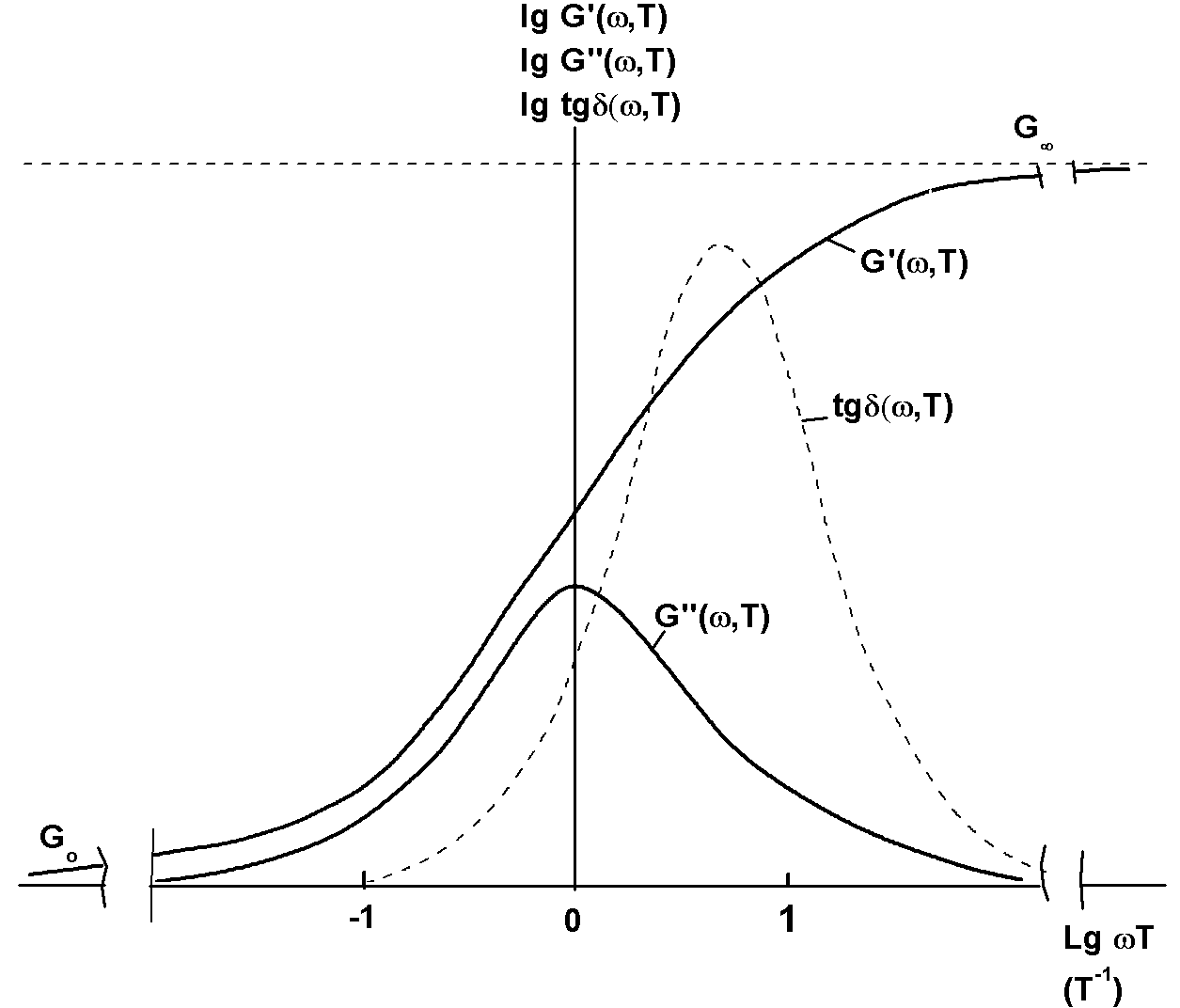
Рис.2.4. Схематическое изображение функций G’(ω), G”(ω) и tgδ(ω) вязко-упругого тела с одним временем релаксации в логарифмических координатах.
Функции G”(ω) и tgδ(ω)
при ωθ, близком к единице, проходят
через максимум, а при ω→0 и ω→∞ стремятся
к 0. Максимум функции G΄΄(ω)
соответствует ωθ=1, а его высота
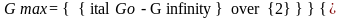 .
Максимум функции tgδ(ω)
соответствует ωθ1=1, где
.
Максимум функции tgδ(ω)
соответствует ωθ1=1, где
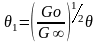 ,
а его высота
,
а его высота
 .
.
Для обобщенной модели линейного вязко-упругого тела, представляющей собой бесконечное число параллельно соединенных элементов Максвелла и одной мягкой пружины с модулем G∞ и имеющей бесконечный набор (спектр) времен релаксации, функции G΄(ω) и G΄΄(ω), аналогично квазистатическим функциям G(t), выражают или в дискретной, или интегральной формах (см. уравнения 2.15 и 2.17), соответственно, как сумму вкладов отдельных элементов или с использованием подинтегральной непрерывной функции распределения времен релаксации F(θ):
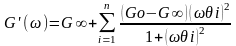 (2.40)
(2.40)
 (2.41а)
(2.41а)
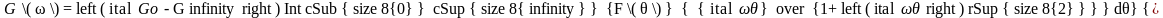 (2.42а)
(2.42а)
Функция распределения времен релаксации F(θ), как уже указывалось при анализе квазистатических режимов (см.с.7-8), представляет собой набор точек с аргументом θk и ординатами G΄k и G΄΄k и является обобщенной характеристикой вязко-упругости среды при динамических гармонических режимах, причем выражение F(θ)dθ имеет размерность модуля. Определить эту функцию при динамических режимах можно по известным кривым G΄(ω) или G΄΄(ω) в широком интервале частот, которые, в свою очередь, можно получить по экспериментальным данным для сравнительно узкого интервала ω, но в широком интервале температур с использованием принципа температурно-временной аналогии для построения так называемых «обобщенных» кривых G΄(ω) или G΄(ω) (см.раздел….). При использовании таких кривых в логарифмической шкале частот уравнения (2.41а) и (2.42а) записываются с использованием логарифмической функции распределения времен релаксации H(θ), равной θF(θ):
 (2.41б)
(2.41б)
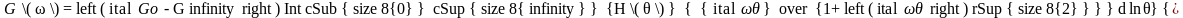 (2.42б
(2.42б
Для приближенной оценки функций F(θ) и H(θ) по кривым G΄(ω) или G΄(lnω) подинтегральное выражение в уравнении (1.38) заменяют на ступенчатую функцию, и функции F(θ) и H(θ) определяют по наклону кривых G΄(ω) или G΄(lnω) в точке, в которой ωθ=1. [Тоб.с.126].
б) Монотонная нагрузка/разгрузка с заданной скоростью
При монотонном нагружении с постоянной скоростью деформирования Vd кривая напряжение – деформация τ(γ) для модели стандартного вязко-упругого тела (см.Рис.2.2а) описывается соотношением [Фр.с.218]:
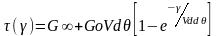 (2.43)
(2.43)
В полном цикле нагрузки/разгрузки кривые τ(γ) образуют гистерезисную петлю, площадь которой соответствует энергии деформирования ΔW, необратимо рассеиваемой за цикл, а общая площадь под кривой разгрузки – упругой энергии W, обратимо накапливаемой в цикле нагружения:
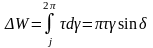 ;
;
 (2.44)
(2.44)
Отношение ΔW к W определяет коэффициент гистерезисных потерь κ, связанный с тангенсом угла механических потерь при гармонических колебаниях соотношением:
 , (2.45)
, (2.45)
т.к. при малом δ sinδ ≈ tgδ.
Кажущийся модуль упругости в цикле
нагрузки/разгрузки определяется по
наклону касательной к соответствующей
кривой в заданной точке. Коэффициент
гистерезисных потерь и кажущийся модуль
упругости являются функциями скорости
деформирования при нагружении или
разгрузке. При
 ,
где γ – заданная относительная деформация,
θ – время релаксации напряжения,
наблюдается максимум коэффициента
гистерезисных потерь и перегиб на кривой
G(Vd).
При Vd→0
G(Vd)→G∞,
а при Vd→∞
G(Vd)→G0.
Коэффициент κ(Vd)
в обоих случаях стремится к 0.
,
где γ – заданная относительная деформация,
θ – время релаксации напряжения,
наблюдается максимум коэффициента
гистерезисных потерь и перегиб на кривой
G(Vd).
При Vd→0
G(Vd)→G∞,
а при Vd→∞
G(Vd)→G0.
Коэффициент κ(Vd)
в обоих случаях стремится к 0.
в) Свободно-затухающие колебания
Свободно-затухающие колебания описываются как колебания классического осциллятора единичного объема, связанного с внешней массой m. На практике режимы свободно-затухающих колебаний обычно реализуют с помощью крутильных или изгибных («язычковых») маятников. В резко выраженных упруго-вязких средах затухание таких колебаний происходит практически мгновенно, поэтому эти режимы для их исследований не применяются. Применительно к вязко-упругой среде в виде модели стандартного вязко-упругого тела (см. Рис.2.2а) уравнение движения при свободных затухающих колебаниях имеет вид [Тоб.с.109]:
 , (2.47)
, (2.47)
где ηd и Gd - динамические вязкость и модуль упругости как функции скорости деформирования или частоты колебаний.
Решение уравнения (2.47) для деформации как функции времени после придания модели начальной деформации γ(0) имеет вид:
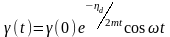 ,
(2.48)
,
(2.48)
В этом уравнении круговая частота свободно-затухающих колебаний, не зависящая для линейной вязко-упругой модели от амплитуды колебаний, связана с Gd и ηd соотношением:
 (2.49)
(2.49)
При малом вкладе вязкого компонента (ηd→0) для заданной частоты:
Gd= =G΄=η”ω (2.50)
=G΄=η”ω (2.50)
Отношение амплитуд последовательных колебаний системы описывается экспонентой:
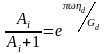 (2.51)
(2.51)
Натуральный логарифм этого отношения называется логарифмическим декрементом затухания свободных колебаний Δ:
 (2.52)
(2.52)
Декремент затухания для линейной вязко-упругой модели связан с коэффициентом гистерезисных потерь при циклической нагрузке/разгрузке κ и tgδ при гармонических колебаниях следующими соотношениями:
Δ =κ=2πtgδ (2.53)
Непосредственная связь параметров вязко-упругости в режиме свободно затухающих колебаний для линейных вязко-упругих тел с соответствующими параметрами динамических механических свойств в режиме гармонических колебаний позволяет перенести все соотношения для частотных зависимостей этих свойств на параметры свободно-затухающих колебаний.
г) Распространение и поглощение упругих (звуковых и ультразвуковых) колебаний (волн)
При распространении упругих колебаний в линейной вязко-упругой среде в направлении оси x уравнение, описывающее смещение частиц среды в этом направлении Y(x), имеет вид уравнения движения плоской волны со скоростью с [Френк.с.230]:
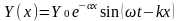 , (2.54)
, (2.54)
где Y0 – начальная амплитуда колебаний; α –коэффициент затухания волны (поглощения звука) по расстоянию; ω – круговая частота (ω=2πν, ν – периодическая частота); k =2π/λ – волновое число (λ – длина волны).
Скорость распространения упругих волн при этом равна: с=νλ (2.55)
Ее величина в изобарно-изотермических условиях определяется упругими параметрами среды, зависящими от частоты, а также типом упругих колебаний – продольных (с растяжением/сжатием среды) и поперечных (сдвиговых). В неограниченной сплошной среде, в которой реализуется объемно-напряженное (плоско-деформированное) состояние, скорости продольных (сl) и сдвиговых (сt) волн равны и связаны с реальными компонентами динамических комплексных модулей при объемном растяжении/сжатии (К΄) и при сдвиге (G΄), а также с плотностью среды ρ соотношением:
 (2.56)
(2.56)
При распространении упругих колебаний в тонких стержнях, в которых реализуется плоско-напряженное состояние, скорость распространения продольных и поперечных волн определяются только соответствующими динамическими модулями упругости (E΄ и G΄ соответственно) и плотностью среды:
 ;
;
 (2.57)
(2.57)
Для сдвиговых волн с учетом функции G΄(ω) (уравнение 2.37) при условии что G∞<G0 выражение для частотной зависимости скорости звука имеет вид:
 (2.58)
(2.58)
где
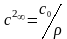 ;
;
 - скорости звука при очень высоких (ω→∞)
и низких(ω→0) частотах. Эта функция, как
и G΄(ω) претерпевает перегиб
при ωθ=1.
- скорости звука при очень высоких (ω→∞)
и низких(ω→0) частотах. Эта функция, как
и G΄(ω) претерпевает перегиб
при ωθ=1.
Коэффициент вязко-упругого затухания упругих колебаний и волн по расстоянию α также является функцией частоты и при заданной частоте связан с параметрами механических потерь при гармонических колебаниях следующими соотношениями:
 (2.59)
(2.59)
С учетом уравнений (2.38) и (2.59) функцию α(ω) можно получить в следующем виде:
 , (2.60)
, (2.60)
где
 - коэффициент затухания звука как функция
частоты на одну длину волны. Эта функция,
как и показатели механических потерь
при гармонических колебаниях, проходит
через максимум при ωθ=1.
- коэффициент затухания звука как функция
частоты на одну длину волны. Эта функция,
как и показатели механических потерь
при гармонических колебаниях, проходит
через максимум при ωθ=1.
Кроме коэффициента затухания звука по расстоянию используется также показатель, характеризующий затухание звуковых колебаний и волн во времени – коэффициент β(ω). Коэффициенты α и β связаны между собой (при одинаковой частоте) соотношением:
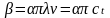 (2.61).
(2.61).
II.1.3. Реологические состояния аморфных полимеров и релаксационные (механические реологические) переходы в них.
Реологические состояния ПМ в однофазном аморфном состоянии характеризуют типы их деформационного поведения и определяются преимущественным проявлением (доминированием) при заданных температурно-временных условиях нагружения или деформирования одного из трех основных видов деформаций: вязкого течения, замедленных и мгновенных упругих деформаций. Преимущественное проявление вязкого течения определяет вязко-текучее состояние, а замедленных и мгновенных упругих деформаций, соответственно, высокоэластическое и стеклообразное состояния.
Как следует из феноменологических и молекулярно-кинетических представлений об обобщенном механическом деформационном поведении полимеров как вязко-упругих и упруго-вязких сред, с кинетической, или релаксационной точки зрения их реологические состояния определяются соотношениями временных условий (длительности t или частоты ) нагружения или деформирования и характерного временного параметра (времени релаксации) процесса, обусловливающего соответствующий вид деформации. Замедленные упругие (высокоэластические) деформации и деформации вязкого течения полимеров в аморфном однофазном состоянии определяются наиболее медленными крупномасштабными формами молекулярного теплового движения – кооперативным сегментальным движением, или α-формой с временем релаксации θα и связанным с ним макроброуновским движением цепей как целого с макроскопическим временем релаксации θm соответственно, а мгновенно упругие – быстрыми мелкомасштабными формами молекулярного теплового движения, в первую очередь высокочастотными тепловыми колебаниями. Очевидно, что в таком случае вязко-текучее состояние ПМ в аморфном однофазном состоянии соответствует условиям проявления макроброуновского движения (t/θm>1 или ωθm<1), высокоэластическое - отсутствию (заторможенности) макроброуновского движения и проявлению α-формы сегментального движения (t/θm<1 или t/θα>1 и ωθm>1 или ωθα<1 соответственно), а стеклообразное - заторможенности α-формы сегментального движения (t/θα<1 или ωθα>1). При этом вязко-текучее состояние может проявляться только в случае линейных или разветвленных макромолекул при отсутствии непрерывной сетки физических зацеплений цепей, а высокоэластическое, наоборот, в случае полимеров со стабильной сетчатой структурой, образованной соединением цепей ковалентными связями («химические» сетки) или термодинамически стабильными физическими узлами («физические» сетки). В стеклообразном состоянии могут находиться полимеры любой молекулярной топологии. После замораживания α-формы сегментального движения в стеклообразном состоянии сохраняющиеся мелкомасштабные формы микроброуновского движения (β,γ,δ) могут обусловливать дополнительные реологические подсостояния стеклообразного состояния: β ( при t/θβ>1 или ωθβ<1), γ (при t/θγ>1 или ωθγ<1) и δ (при t/θδ>1 или ωθδ<1). Истинно стеклообразное состояние с проявлением мгновенно упругих деформаций возможно только после замораживания всех форм сегментального движения.
Изменения доминирующего типа и характера деформаций при изменении временных условий нагружения или деформирования или вследствие изменении типа и характера протекающих релаксационных процессов и, соответственно, изменения времен релаксации приводят к релаксационному переходу из одного реологического состояния в другое. В соответствие с феноменологическими представлениями (см. раздел 2.1) изменение типа и характера деформаций в вязко-упругих средах проявляется при соотношении t/θ или произведении ωθ, близком к 1 (в пределах одного десятичного порядка), поэтому за условие релаксационного перехода принято равенство единице отношения t/θ или произведения ωθ. В этом случае условиями основных релаксационных переходов (из вязко-текучего в высокоэластическое состояние, т.е l,l–перехода, проявления или потери текучести и из высокоэластического в стеклообразное, т.е. α-перехода, стеклования или размягчении) являются t/θm=1 или ωθm=1 и t/θα=1 или ωθα=1 соответственно. Релаксационные переходы, связанные с мелкомасштабными формами микроброуновского движения (β,γ,δ), относятся к дополнительным, или вторичным переходам в стеклообразном состоянии, и их условиям являются равенства единице отношений t или произведений ω на соответствующие времена β,γ и δ релаксации .
Из t/θ и ωθ условий нахождения в различных реологических состояниях и релаксационных переходов в полимерах в аморфном однофазном состоянии следует, что эти состояния и переходы могут обусловливаться как временами релаксации соответствующих форм сегментального теплового движения, зависящими от термодинамических параметров состояния (температуры, давления, состава) и структурных превращений при их изменении, так и временными условиями нагружения или деформирования (t,ω), т.е. как термодинамическими и структурными (геометрическими), так и чисто кинетическими факторами.
При заданных временных условиях
нагружения или деформирования, которые
в реальных условиях соответствуют
временам t больше с
и частотам ω меньше
с
и частотам ω меньше Гц,
реологические состояния и релаксационные
переходы в полимеров в аморфном однофазном
состоянии с заданной молекулярной
топологией определяются только
термодинамическими факторами, в первую
очередь температурой, влияющей (при
отсутствии термохимических превращений)
на молекулярную подвижность непосредственно
или вследствие микроструктурных
превращений на надмолекулярном уровне
при ее изменении. С классической
молекулярно-кинетической точки зрения
при понижении температуры все формы
теплового движения замедляются, т.е.
увеличиваются их времена релаксации,
вследствие чисто температурных эффектов,
связанных с уменьшением энергии теплового
движения по отношению к потенциальному
барьеру (энергии активации) процесса
ΔЕ в соответствие с уравнением Аррениуса
[ ]:
Гц,
реологические состояния и релаксационные
переходы в полимеров в аморфном однофазном
состоянии с заданной молекулярной
топологией определяются только
термодинамическими факторами, в первую
очередь температурой, влияющей (при
отсутствии термохимических превращений)
на молекулярную подвижность непосредственно
или вследствие микроструктурных
превращений на надмолекулярном уровне
при ее изменении. С классической
молекулярно-кинетической точки зрения
при понижении температуры все формы
теплового движения замедляются, т.е.
увеличиваются их времена релаксации,
вследствие чисто температурных эффектов,
связанных с уменьшением энергии теплового
движения по отношению к потенциальному
барьеру (энергии активации) процесса
ΔЕ в соответствие с уравнением Аррениуса
[ ]:
 , (3.1)
, (3.1)
где: θ0 – предэкспоненциальный множитель, соответствующий периоду элементарного акта данного процесса. Применительно к наиболее крупномасштабной α-форме сегментального движения в полимерах лучше температурную зависимость времени релаксации по сравнению с активационной теорией дает теория свободного объема, в соответствие с которой уменьшение времени релаксации сегментального движения с понижением температуры обусловлено уменьшением флуктуационного свободного объема, или объема, в котором совершается данная форма теплового движения.
Базирующееся на этой теории уравнение Вильямса, Ланделла и Ферри (ВЛФ) для α-формы сегментального движения имеет вид [ ]:
 (3.2)
(3.2)
где: θα(Т) и θα(Тr) – времена релаксации α формы сегментального движения при температуре Т и температуре отсчета (приведения) Tr соответственно; С1, С2 – универсальные постоянные, не зависящие от типа полимера и определяемые выбором Тr: при Тr, равной температуре, при которой доля свободного объема данного полимера (φv) равна 0,025 (в теории свободного объема эта температура соответствует замораживанию сегментального движения, т.е. экспериментально наблюдаемой температуре стеклования Тg) C1=17,44, а С2 =51,6 К, а при Тr, равной температуре Ts, при которой доля свободного объема φv данного полимера равна этой доле в полиизобутилене при 243 К, C1=8,86, а С2 =101,6К [Тоб. с.93].
Вблизи критических точек Tcr, в одной из которых формируется непрерывная сетка полимерных цепей в результате их связывания за счет механических зацеплений или в твердоподобных кластерах с проявлением l,l-переход (вблизи Тm), а в другой формируется непрерывный кластера или плотная упаковка твердоподобных доменов и проявляется структурное стеклование (вблизи То или Т2), соответствующие времена релаксации макроброуновского движения (θm) и α-формы сегментального движения (θα) зависят от температуры по степенной функции с универсальным показателем степени ν, близким к единице (уравнению Фогеля, Фалчера и Таммана, ФФТ )[ ]:
 (3.3)
(3.3)
Это свидетельствует о том, что образование вблизи критических точек Тm,То или Т2 непрерывных кластеров (сетки связанных цепей и упаковки твердоподобных доменов соответственно) являются, в соответствие с теорией протекания, или перколяции, перколяционными переходами, а сами кластеры имеют фрактальную структуру, и в соответствие с принципом масштабной инвариантности их поведение описывается скейлинговыми соотношениями.
При температуре выше гипотетической температуры фазового перехода 1-го рода Тf1 и критической температуры Тm вплоть до температуры начала деструкции цепей, т.е. в термодинамически стабильном состоянии до формирования непрерывной сетки физических лабильных узлов, или зацеплений цепей в ПМ в аморфном однофазном состоянии с линейной или разветвленной макромолекулярной топологией основным видом деформаций при заданных временных условиях нагружения или деформирования является вязкое течение и, соответственно, фазы находятся в вязко-текучем реологическом состоянии. При этом уравнение Аррениуса достаточно хорошо описывает температурную зависимость макроскопического времени релаксации θm. При приближении к критической температуре Тm макроскопическое время релаксации θm или связанное с ним «время жизни» зацеплений в соответствие с уравнением ФТТ (уравнением 3.3) сингулярны, т.е. стремятся к бесконечности, поэтому очевидно, что при любых реальных условиях эксперимента условия релаксационного перехода из вязко-текучего в высокоэластическое состояние (t/θm=1 или m=1) достигаются при некоторой температуре (температуре потери текучести Тт), которая всегда выше критической температуры Тm. Таким образом, структурная (геометрическая) природа потери текучести в результате образования непрерывной сетки зацеплений и перехода в высокоэластическое состояние в реальных условиях экспериментов, в том числе в методах МР, скрыта кинетическими эффектами.
В высокоэластическом состоянии при ограниченном макроброуновском движении в результате образования стабильной непрерывной сетки основной формой теплового движения является кооперативное сегментальное движение (α-форма) и, соответственно, проявляются процессы α-релаксации. ПМ в аморфном однофазном состоянии с линейной или разветвленной макромолекулярной топологией переходят в это состояние при температуре ниже Тт и находятся в нем вплоть до стеклования. Однофазные аморфные ПМ с сетчатой макромолекулярной топологией находятся в этом состоянии при любой температуре выше Тс вплоть до температуры начала деструкции. При Т›Тf1, т.е. в термодинамически стабильном состоянии, температурная зависимость времени релаксации α-формы сегментального теплового движения описывается уравнением Аррениуса, причем энергии активации этой формы сегментального движения близка по величине к энергии активации макроброуновского движения в вязко-текучем состоянии, что свидетельствует об определяющей роли сегментальной подвижности в движении цепей в целом. При Т‹Тf1 и особенно при приближении к Тс, т.е. в метастабильном состоянии, эти зависимости лучше описываются теорией свободного объема и уравнением ВЛФ (уравнением 3.2), т.к. наличие твердоподобных доменов в этом состоянии резко повышает энергию активации сегментального движения и делают ее зависимой от температуры.
В сильно переохлажденном метастабильном состоянии с приближением к критической температуре Т0 или Т2, при которой в соответствие с термодинамическими представлениями резко возрастает вероятность образования в ПМ в аморфном однофазном состоянии непрерывного кластера или плотной упаковки твердоподобных доменов, зависимость θα(Т) описывается уравнением ФФТ (3.3)[ ], и при Т→ Tcr время релаксации θα→∞. Поэтому очевидно, что при любых временных условиях эксперимента условия стеклования (t/θα=1 или =1) выполняются при некоторой температуре (Тс), которая всегда выше критической температуры, т.е. термодинамически обусловленные структурные эффекты в реальных условиях экспериментов, в том числе в методах МР, в процессе стеклования перекрываются кинетическими эффектами и могут проявляться только косвенно в условиях длительного отжига при температуре ниже Тс.
После перехода в стеклообразное состояние с замораживанием кооперативного сегментального движения температурные зависимости времен релаксации сохранившихся мелкомасштабных (β,γ,δ) форм микроброуновского движения обычно описываются уравнением Аррениуса, причем энергия активации этих форм сегментального теплового движения значительно меньше, чем макроброуновского и кооперативного сегментального теплового движения, и соответствующие им β-, γ- и δ-релаксационные переходы значительно меньше по масштабу по сравнению с α-переходом.
Таким образом, полимеры в аморфном
однофазном термодинамически стабильном
и метастабильном состояниях в зависимости
от температуры при заданных временных
условиях механического воздействия,
давлении и составе могут находиться в
трех основных реологических состояниях:
вязко-текучем, высокоэластическом и
стеклообразном и способны претерпевать
при охлаждении два основных релаксационных
перехода: из вязко-текучего в
высокоэластическое состояние (l,l-переход,
или потеря/появление текучести) и из
высокоэластического в стеклообразное
состояние (α-переход, или стеклование/
размягчение) и несколько дополнительных,
или вторичных релаксационных переходов
в стеклообразном состоянии. Значительный,
но скрытый вклад в реологическое
поведение и релаксационные переходы
за счет резкого замедления основных
форм молекулярного теплового движения
в однофазных аморфных ПМ в метастабильном
состоянии вносят термодинамически
обусловленные структурные превращения
- образование непрерывной сетки полимерных
цепей за счет зацеплений, или лабильных
узлов и связывания цепей в твердоподобных
доменах, а также образование непрерывного
кластера или плотной упаковки таких
доменов вблизи критической точки. При
этом типы и количество реологических
состояний и релаксационных переходов
в решающей степени определяются
топологией и длиной полимерных цепей
(Рис. 3.1).
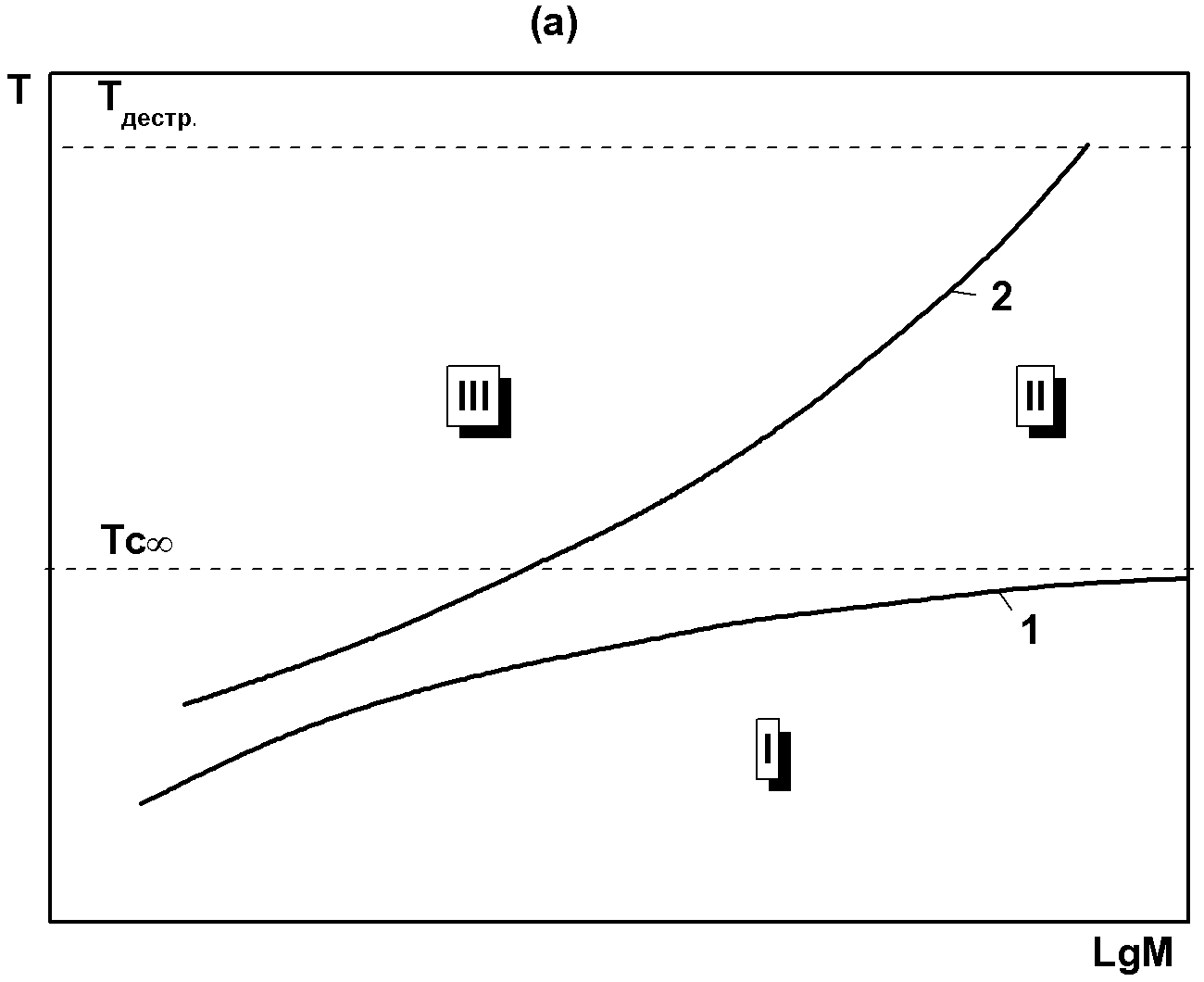
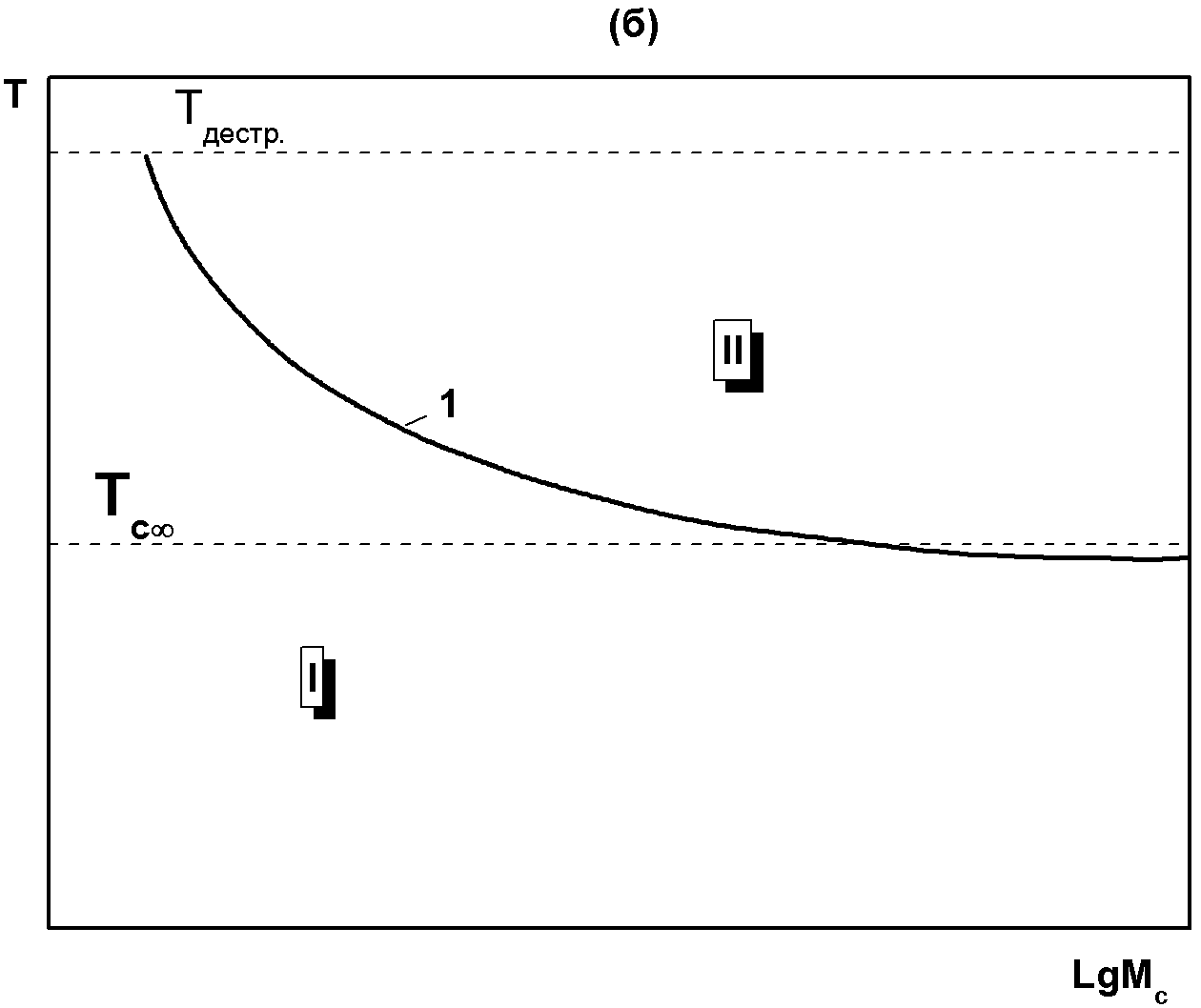
Рис.3.1. Схематические диаграммы реологических состояний (I, II, III– области стеклообразного, высокоэластического и вязко-текучего состояния соответственно) и температурных переходов (1,2 - линии стеклования и l,l-перехода соответственно) в термодинамически стабильном и метастабильном состояниях однофазного аморфного линейного (а) и сетчатого (б) полимеров в координатах температура - молекулярная масса (Мn и Мс соответственно), где Мn - молекулярная масса линейных макромолекул, Мс – молекулярная масса цепей между узлами сетки сетчатых полимеров при заданных временных условиях нагружения или деформирования.
В случае линейных и разветвленных макромолекул (см. Рис.3.1а) возможны все основные реологические состояния и релаксационные переходы, причем существование высокотемпературных состояний и переходов лимитируется только соотношением температуры перехода и температуры термической или термоокислительной деструкции макромолекул. Температура l,l-перехода, или температура текучести Tт неограниченно возрастает с увеличением молекулярной массы, а температура α-перехода (Tα), т.е. экспериментально наблюдаемая температура стеклования (Тс), возрастает до некоторого предельного значения Тс∞ при М→∞. Очевидно, что решающую роль при этом играет уменьшение числа концевых, более подвижных по сравнению с центральными, звеньев. Сетчатые аморфные фазы ПМ и ПМК могут находиться только в стеклообразном или высокоэластическом состояниях с переходом между ними (см. Рис. 1.6б), если их Тс меньше температуры деструкции, а если она выше этой температуры – то только в стеклообразном состоянии. Экспериментально наблюдаемая температура стеклования резко возрастает с уменьшением длины цепей между узлами сетки (увеличением ее густоты) от своего наименьшего значения Тс∞ при Мс→∞, очевидно, за счет увеличения количества связанных концов цепей при уменьшении их длины.
Релаксационные переходы в термодинамически стабильном и метастабильном состояниях аморфных фаз ПМ, обусловленные изменениями соответствующих времен релаксации при заданных временных условиях нагружения или деформирования, возможны не только при изменении температуры (при постоянном давлении и составе), но и при изменении состава, например в результате химических превращений (при постоянных температуре и давлении). На рис. 3.2 схематически изображена обобщенная диаграмма реологических состояний и релаксационных переходов, обусловленных химическими превращениями, так называемая хемореологическая диаграмма отверждаемых, или сшиваемых по ступенчатому механизму реакционноспособных полимерных композиций, претерпевающих переходы из вязко-текучего в высокоэластическое состояние (при Т›Тс композиции) при возникновении непрерывной полимерной сетки (в точке гелеобразования) и из высокоэластического состояния в стеклообразное при достижении температурой стеклования композиции в результате возрастания молекулярной массы полимера (до точки гелеобразования) и густоты сетки (после точки гелеобразования) величины, равной температуре отверждения или больше ее.
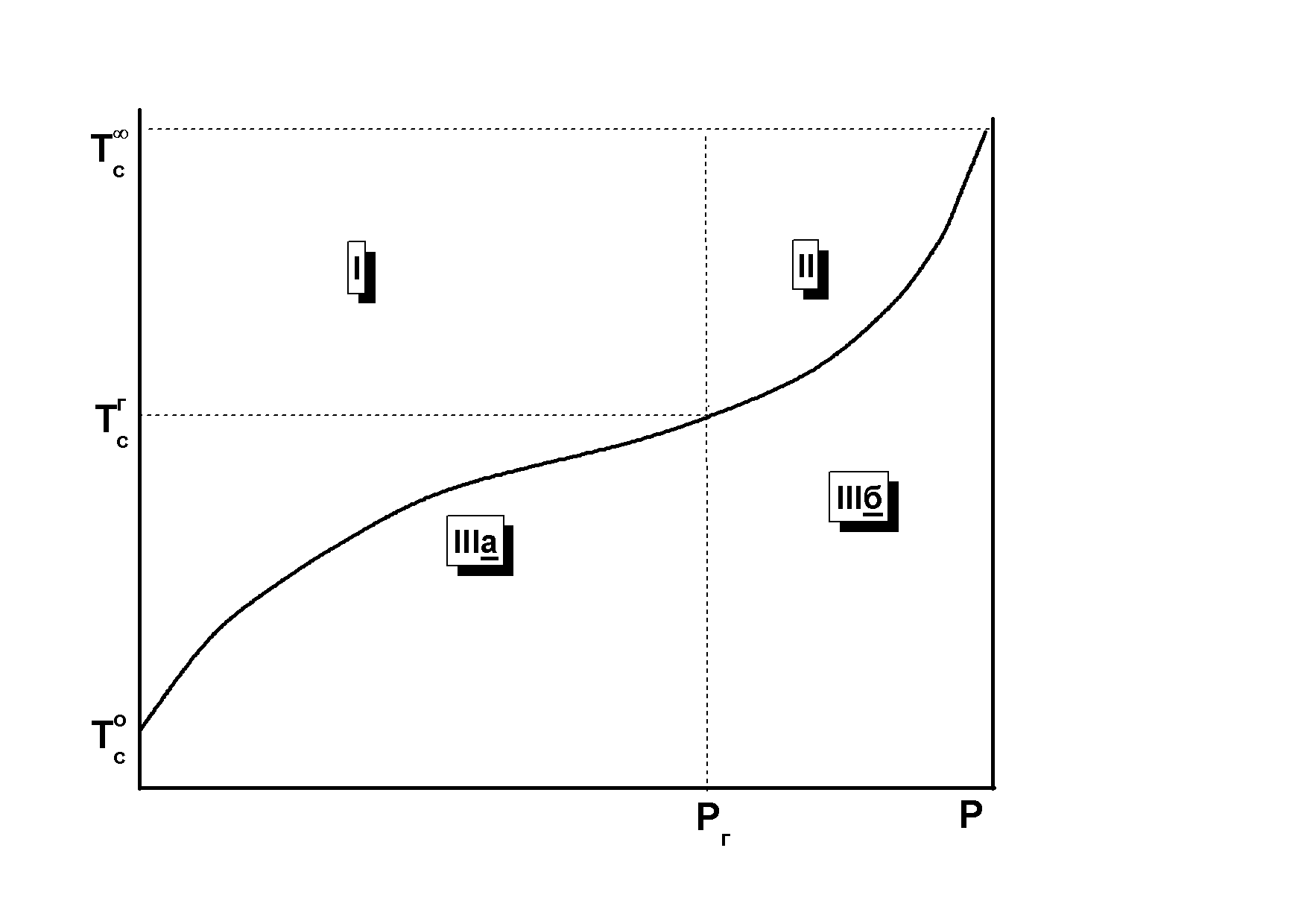
Рис.3.2. Схема обобщенной диаграммы реологических состояний (I, II, IIIа и IIIб -области вязко-текучего, высокоэластического и стеклообразного состояний до и после точки гелеобразования соответственно) и релаксационных переходов (1,2 - линии потери текучести, или гелеобразования и стеклования соответственно) в координатах температура Т – степень превращения р для реакционноспособных полимерных композиций, отверждаемых по ступенчатому механизму: Тс0 , Тсг и Тс∞ - характерные температуры стеклования композиции в начальный момент, в точке гелеобразования и на предельной стадии отверждения соответственно.
Аналогичный вид должна иметь обобщенная диаграмма реологических состояний и релаксационных переходов для растворов линейных или разветвленных полимеров при удалении растворителя в отсутствие фазовых превращений. При этом р должна соответствовать доле полимера в растворе, а Тс0, Тс∞ и Тсг - характерным температурам стеклования растворителя, полимера и концентрированного раствора при возникновении непрерывной сетки зацеплений соответственно.
Поскольку реологические состояния и релаксационные переходы в аморфных полимеров и, соответственно, их вязко-упругое и упруго-вязкое поведение определяются отношением характерного времени нагружения t или произведением частоты приложения нагрузки или деформации ω и времени релаксации соответствующего процесса θ, зависящего только от термодинамических параметров состояния (температуры, давления и состава) и структурных превращений при их изменении, то очевидно, что при заданных термодинамических параметрах состояния изменение реологического состояния, т.е релаксационный переход может происходить по чисто кинетическим причинам, когда условия такого перехода (отношения t/θ или произведения ωθ) достигаются за счет изменения временных условий нагружения или деформирования при заданном времени релаксации соответствующей формы теплового движения. Так, при проявлении макроброуновского и кооперативного сегментального движения с заданными временами релаксации θm и θα соответственно (при Т>Тт) изменение временных условий нагружения или деформирования в широких пределах может сопровождаться чисто кинетическими релаксационными переходами из вязко-текучего состояния в высокоэластическое при t/θm≤1 или ωθm≥1 и в стеклообразное при t/θα≤1 или ωθα≥1. При проявлении только α- формы сегментального движения с заданным θα (при Т>Тс) резкое уменьшение t или увеличение ω может сопровождаться чисто кинетическим релаксационным переходом из высокоэластического в стеклообразное состояние при t/θα≤1 или ωθα≥1, а резкое увеличение t или уменьшение ω – из высокоэластического в вязко-текучее (при конечной форме макромолекул). При замороженном кооперативном сегментальном движении (в стеклообразном состоянии) изменение временных условий нагружения или деформирования в широких пределах может вызывать чисто кинетически только вторичные релаксационные β-,γ- и δ-переходы. Переходы в высокоэластическое и вязко-текучее состояние при этом теоретически возможны только при бесконечно большом времени t или малой частоте ω.
Таким образом, в общем случае к описанию реологических состояний и релаксационных переходов в аморфных полимерах применим принцип соответствия, или аналогии эффектов изменения параметров состояния Т, р и с (при отсутствии структурных превращений) и временных условий внешних воздействий (t или ω), в частности принцип температурно-временной (T-t) или температурно-частотной (Т-) аналогии. В соответствии с этим принципом понижение температуры, увеличивающее время релаксации, дает при прочих равных условиях эффект, аналогичный уменьшению характерного времени внешнего воздействия или увеличению частоты, и наоборот. Этот принцип позволяет, в частности, выявлять влияние временных условий нагружения или деформирования на температуру релаксационных переходов, определяемых методами МР (повышение температуры перехода при уменьшении характерного времени t или повышении частоты ω), а по характерным временам (частотам) внешнего воздействия или температурах, при которых проявляются релаксационные переходы при заданных температурах или временах (частотах) соответственно, определять параметры молекулярного теплового движения. В заданном реологическом состоянии принцип T-t или Т- аналогии позволяет получать обобщенные кривые параметров вязко-упругих или упруго-вязких свойств аморфных фаз ПМ и ПМК в широком интервале t или при выбранной температуре по экспериментальным данным, полученные в узком интервале t или при большом наборе температур (времен релаксации), и наоборот (см. Раздел 2.3.3).
3.2. Обобщенные механические релаксационные спектры полимеров в однофазном аморфном состоянии
Из предыдущего раздела следует, что полимеры в однофазном аморфном состоянии, обладая широким набором форм (спектром) молекулярного теплового движения различного масштаба и многообразными релаксационными переходами, зависящими от термодинамических параметров состояния (температуры, давления и состава) и временных (частотных) условий механического воздействия, должны отличаться сложным реологическим поведением, т.е. иметь сложные механические релаксационные спектры - зависимости вязко-упругих или упруго-вязких свойств от времени или частоты механических воздействий при заданных термодинамических параметрах состояния (временные или частотные спектры) и от температуры, степени превращения или концентрации компонентов при заданных временных или частотных условиях механического воздействия (температурные, хемореологические или концентрационные спектры соответственно). Обобщенные схемы таких спектров приведены на Рис.3.3а,б в логарифмических координатах квазистатических и динамических параметров вязко-упругих свойств и соотношений t/θα и ωθα соответственно:
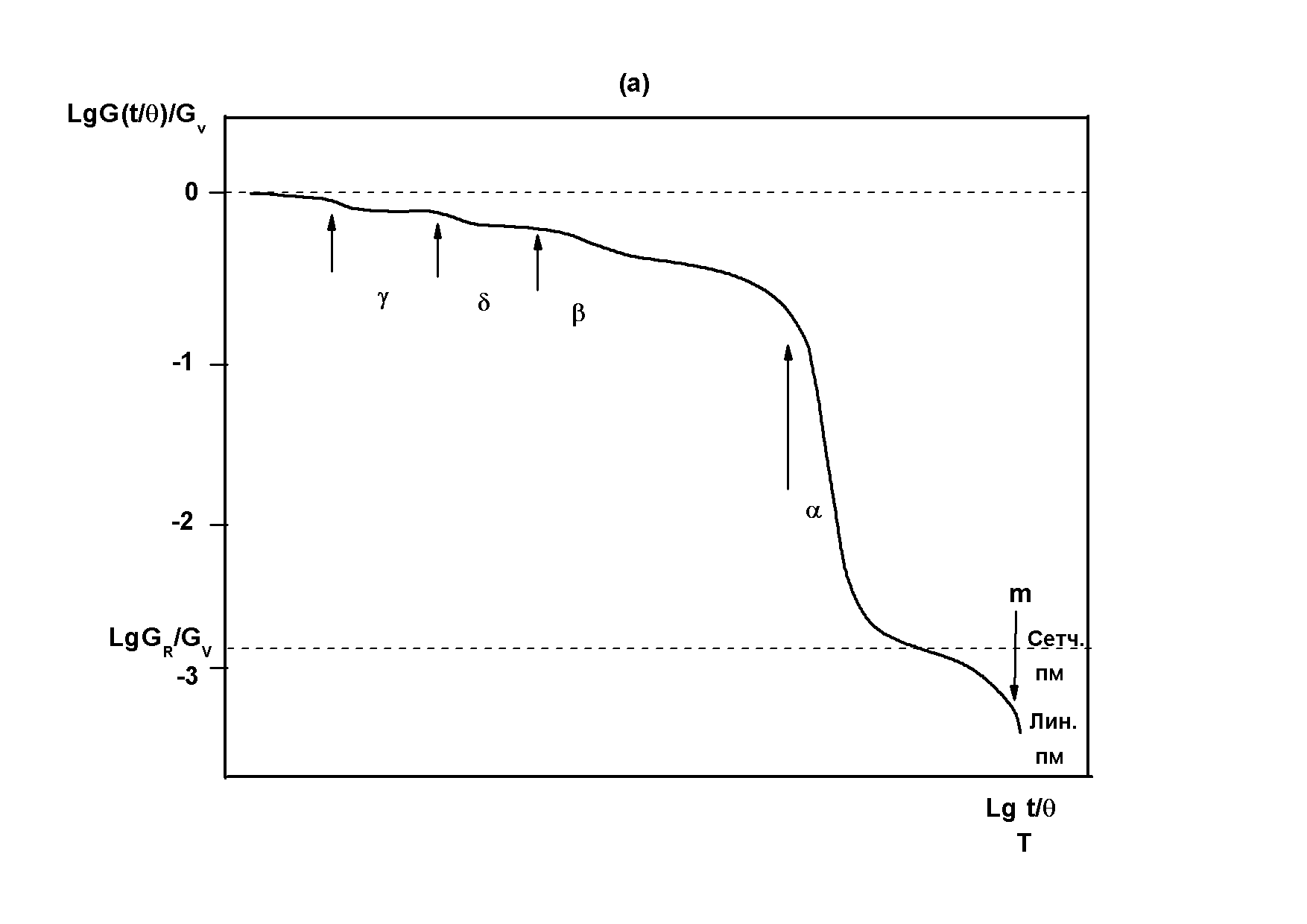
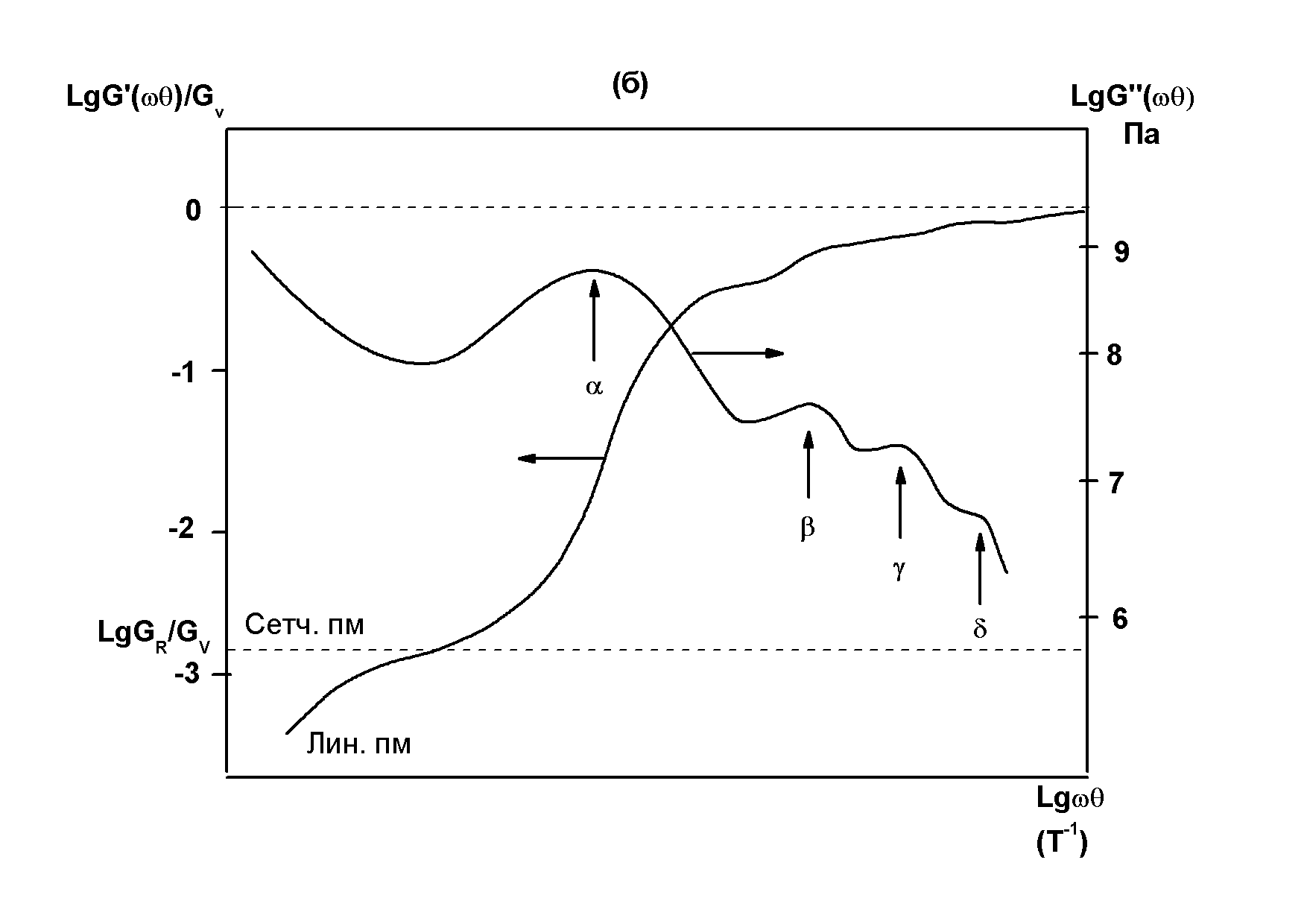
Рис.3.3. Обобщенные схемы механических спектров однофазных аморфных полимеров: а - в квазистатическом режиме, где G(t,Т) – функция релаксации, или релаксационный модуль как функция соотношения длительности внешнего воздействия и времени релаксации θ; б - в динамическом гармоническом режиме, где G′(ω,Т), G″ (ω,Т) – динамические модули упругости и потерь, соответственно, как функции произведения частоты и и времени релаксации θ (Go–модуль мгновенной упругости, G∞ - равновесный модуль задержанной упругости (высокоэластичности), m-,α-,β-,γ-,δ-области релаксационных переходов, соответствующие равенству единице t/θi или ωθi).
На температурных, хемореологических или концентрационных спектрах (при заданных t или ω) повышение температуры, степени отверждения или концентрации полимера соответствует увеличению θ и наоборот. При этом уменьшение t или увеличение ω уменьшает разрешение спектров, т.е. сближает и накладывает друг на друга области релаксационных переходов вследствие различия в энергии активации соответствующих релаксационных процессов (ΔEm≤ΔEα›ΔEβ›ΔEγ›ΔEδ). В случае временных или частотных спектров (при заданной температуре, степени отверждения или концентрации полимера) аналогичный эффект оказывает уменьшение термодинамических параметров композиций, в первую очередь, понижение температуры.
В механической релаксационной спектрометрии однофазных аморфных полимеров обычно получают экспериментально обобщенные температурные, временные или частотные механические спектры или их отдельные области с использованием различных методов и анализируют их, определяя предельные характеристики вязко-упругих и упруго-вязких свойств: модуль мгновенной упругости Go, равновесный модуль высокоэластичности G∞ и начальную вязкость η0 (см. раздел 1) и непосредственно вязко-упругие (релаксационные) параметры феноменологических соотношений, приведенных в разделе 2.1: средние времена релаксации соответствующих процессов, функции или ширину их распределения.
Средние времена релаксации α-, β-, γ- или δ-процессов в аморфных полимерах определяют по обобщенным температурным, временным или частотным механическим спектрам или их отдельным областям из условий равенства единице t/θ или ωθ (по точкам перегиба на кривых G(t), J(t) или G’(ω) или по максимумам на кривых механических потерь). По температурным зависимостям средних времен релаксации с использованием соответствующих уравнений (1.79-1.80) рассчитывают энергию активации этих процессов или долю флуктуационного свободного объема в них, выявляя таким образом механизм и кинетику молекулярного теплового движения и, соответственно, структуру ПМ и ПМК или ее изменения.
Функции распределения времен релаксации:
простые F(θ) и Ф(θ)
или логарифмические H(θ)
и L(θ) определяют,
соответственно, по наклону кривых G(t),
J(t)
и G΄(ω) или G(lnt),
J(lnt)
и G΄(lnω)
в широких интервалах t
и ω (см. раздел 2.1, уравнения 2.22 – 2.23).
Однако,эти функции, кроме того, что их
трудно определять, являются довольно
искусственными параметрами вязко-упругих
или упруго-вязких свойств, и их сложно
соотнести с реальными процессами
механической релаксации в аморфных
однофазных ПМ [Perez, с.113].
Значительно проще проблема оценки и
учета ширины распределения времен
релаксации соответствующих процессов
решается введением показателей степени,
отличных от единицы и не имеющих четкого
физического смысла, в феноменологические
соотношения, описывающие временные или
частотные зависимости параметров
вязко-упругих или упруго-вязких свойств:
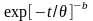 или
или
 для
квазистатических режимов и
для
квазистатических режимов и
![]() или
или
 для
динамических режимов и определением
этих показателей из экспериментально
полученных механических спектров.
Типичным примером может служить уравнение
Гаврильяка для комплексной податливости
[Perez, 28]:
для
динамических режимов и определением
этих показателей из экспериментально
полученных механических спектров.
Типичным примером может служить уравнение
Гаврильяка для комплексной податливости
[Perez, 28]:
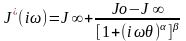 (3.4)
(3.4)
Отклонение показателей степени от единицы характеризует ширину распределения времен релаксации.
II.1.4. Возможности и примеры применения механической релаксационной спектрометрии для исследования молекулярного теплового движения и релаксационных переходов в полимерах
Определение температурных зависимостей деформаций при квазистатическом нагружении и заданных условиях нагревания или охлаждения, так называемых термомеханических кривых, долгое время служило одним из основных методов исследования температурных релаксационных переходов в полимерах (ПМ) [ ]. Использование при этом прибора Лазуркина, основанного на внедрении цилиндрической иглы в образец при непрерывном воздействии сравнительно большой статической нагрузки и изменении температуры с заданной скоростью, обусловливают низкую чувствительность этого метода и затрудняют количественную интерпретацию получаемых результатов. Поэтому классические методы квазистатического нагружения или деформирования (методы ползучести и релаксации напряжения) при различных температурных режимах являются значительно более эффективными с точки зрения исследования релаксационных процессов и переходов в полимерах. Однако эти методы требуют больших затрат времени, поэтому в настоящее время наиболее распространенными и эффективными являются низкочастотные динамические механические методы при вынужденных синусоидальных и свободно-затухающих колебаниях с использованием «язычковых» и маятниковых приборов [ ]. В эти методах могут быть использованы простые в изготовлении образцы материалов требуемого состава, различные типы и величины (амплитуды) нагрузок и деформаций (при сдвиге, растяжении или сжатии), различные температурно-временные условия нагружения и деформирования. В установках могут быть обеспечены практически любые условия окружающей среды и внешние воздействия (жидкие или газообразные среды, воздействие излучений и т.п.), что позволяет проводить исследования непосредственно при воздействии факторов окружающей среды (in situ). Получаемые этими методами температурные зависимости параметров вязко-упругих свойств (показателей упругости и механических потерь) при фиксированной частоте, так называемые изохронные динамические термомеханические кривые (спектры), или, реже, частотные зависимости этих свойств в изотермических условиях (изотермические кривые) несут наиболее полную информацию о механизме и кинетике релаксационных процессов, протекающих в ПМ и непосредственно связанных с молекулярным тепловым движением, структурой и структурными превращениями в них. Динамические механические методы являются наиболее эффективными при исследовании молекулярной подвижности в ПМ с различной молекулярной и надмолекулярной структурой и фазовой морфологией, на различных структурных уровнях, в различных фазовых и реологических состояниях и непосредственно в областях релаксационных переходов. Кроме того, этими методами определяются важнейшие с практической точки зрения параметры технологических и эксплуатационных свойств ПМ (вязкие и упругие компоненты их деформаций, деформационная теплостойкость, демпфирующая способность и другие) при заданных температурно-частотных условиях нагружения и деформирования, других внешних воздействиях и параметрах окружающей среды.
В случае однофазных аморфных (некристаллизующихся) ПМ методы динамической механической релаксационной спектрометрии чаще всего используются для получения обобщенных температурных (изохронных) термомеханических кривых (ТМК) или, реже, временных или частотных (изотермических) механических спектров или их отдельных видов. Такие спектры позволяют определять предельные характеристики вязко-упругих и упруго-вязкостных свойств (модули мгновенной упругости, равновесные модули высокоэластичности и начальная вязкость) по значениям реальных компонент динамического модуля и вязкости при условиях ωθα››1, ωθα‹‹1 и ωθm‹‹1 соответственно, т.е. при мгновенно упругих деформациях в стеклообразном состоянии, равновесных деформациях в высокоэластическом состоянии и установившемся течении в вязко-текучем состоянии, а также параметров l,l-, α-, β-, γ- и δ-процессов механической релаксации и соответствующих им температурных релаксационных переходов (средних времен релаксации, функций их распределения, энергии активации и т.п.
На рис. 4.1 приведен пример динамической ТМК типичного аморфного некристаллизующегося полимера (полиметилметакрилата, ПММА), находящегося при нормальных условиях в стеклообразном состоянии, в широком температурном интервале при частоте 1 Гц, на котором четко проявляются пики потерь всех основных релаксационных переходов.

Рис.4.1. Динамические термомеханические кривые ПММА в широком температурном интервале при частоте 1 Гц: кривые 1 - G΄/Gu, 2- tgδ; l,l, α, β, γ, δ – области соответствующих релаксационных переходов [Perez, с.131]
По динамическим ТМК, полученным наборе частот, с применением принципа температурно-временной аналогии, могут быть рассчитаны обобщенные кривые для широкого интервала частот при выбранной температуре приведения и предельные модули упругости в стеклообразном и высокоэластическом состояниях. По зависимости обратной температуры пика потерь (Тmах) соответствующего релаксационного перехода от частоты ν может быть определена энергия активации релаксационного процесса (зависимость ν - 1/Тmах схематически изображена на вставке к рис.4.1). Определенная таким образом энергия активации для α-релаксации в аморфных ПМ в зависимости от химического строения и длины цепей, определяющей их жесткость, и энергию межмолекулярного взаимодействия, а также от плотности упаковки и других факторов варьируется для α-релаксационного процесса от 120 до 480 кДж/моль, для β –процесса - от 60 до 170 кДж/моль, для γ-процесса – от 30 до 85 кДж/моль и для δ-процесса – от 15 до 45 кДж/моль.
Динамические термомеханические кривые однофазных аморфных ПМ, как и энергия активации основных релаксационных процессов в них, в решающей степени определяется не только химическим строением звеньев, но и топологией полимерных цепей (линейной, разветвленной или сетчатой) и их длиной (молекулярной массой), а также характером упаковки. В случае линейных или разветвленных макромолекул с молекулярной массой выше некоторой критической (порядка 104) увеличение длины цепей практически не сказывается на положении перегиба на кривой модуля и пика показателя потерь в области стеклования (α-релаксации), но достаточно резко проявляется в расширении области высокоэластического состояния (плато высокой эластичности на кривой модуля) и увеличении температуры перехода в вязко-текучее состояние при температуре выше ТС. На рис. 4.2 схематически показаны такие изменения динамических термомеханических спектров линейного аморфного полимера в областях α- и γ-релаксаций при изменении молекулярной массы его цепей:

Рис.4.2. Схематическое изображение динамических термомеханических спектров линейного аморфного полимера в области α-релаксации с более низкой (1,1΄) и более высокой (2,2΄) молекулярной массой: кривые 1,2 - G΄, 1΄,2΄- tgδ; α и γ – области соответствующих релаксационных переходов.
Длина цепей, определяющая долю свободных концевых звеньев, заметно влияет при этом на дополнительные релаксационные процессы и переходы в стеклообразном состоянии, в частности, в области γ-релаксации. В случае сетчатых полимеров уменьшение длины цепей между узлами сетки, т.е. увеличение густоты сетки или частоты ее узлов, проявляется на динамических термомеханических спектрах в смещении перегиба на кривых модуля и пика показателя механических потерь в области стеклования в сторону более высокой температуры, а также в резком повышении модуля в области высокоэластического состояния и снижении высоты пика потерь (Рис. 4.3).
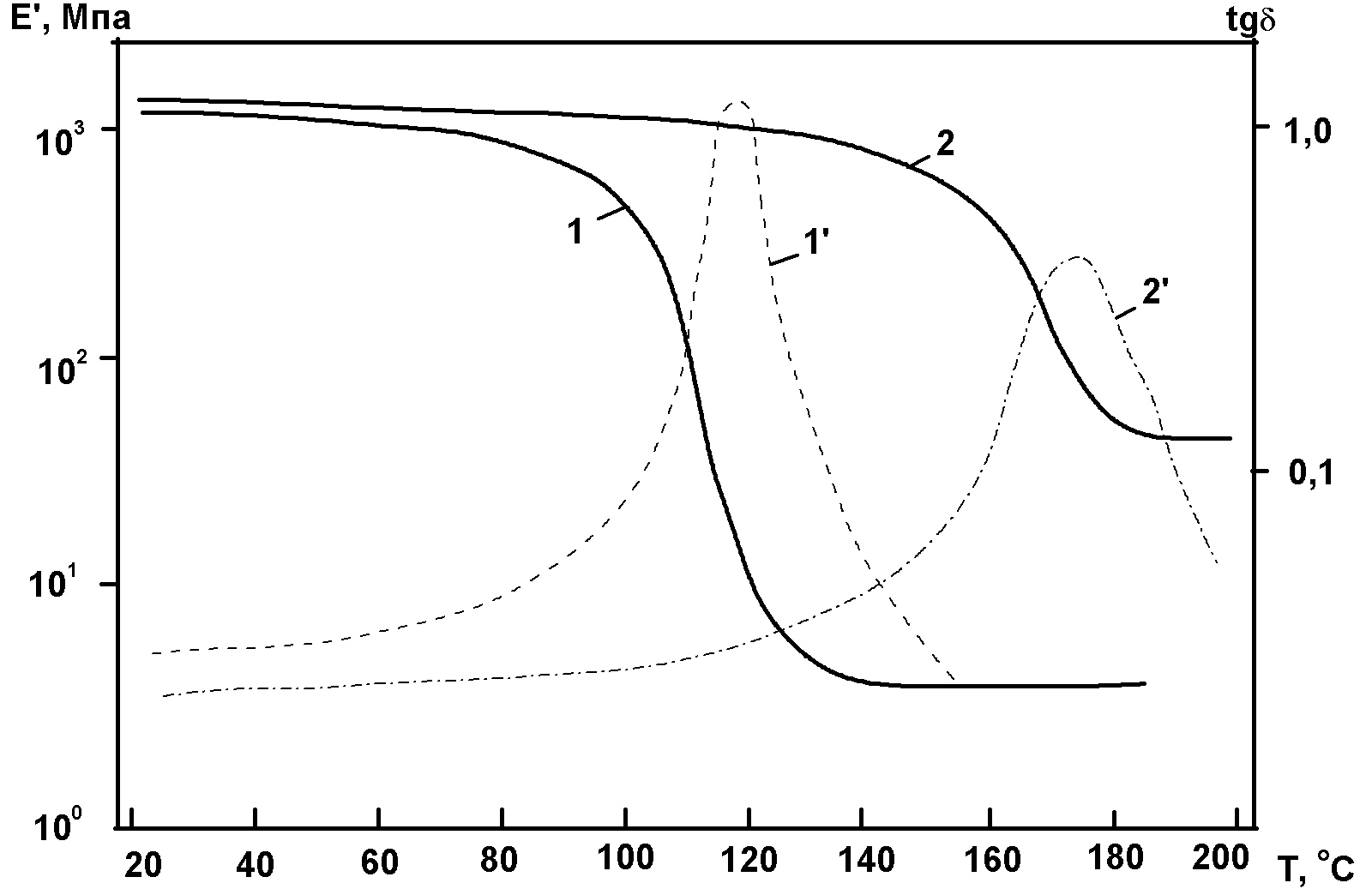
Рис.4.3.Динамические термомеханические спектры в области α-релаксации при частоте 1 Гц эпоксиаминной композиции на основе диглицидилового эфира бисфенола А, или дифенилопропана (ДГЭБА) и диаминодифенилметана (ДДМ), отвержденной различным количеством ДДМ: при 98,5%-м избытке ДДМ (менее густая сетка, кривые 1,1΄) и при недостатке в 2,4% (более густая сетка, кривые 2,2΄) [Нильсен].
Густота сетки, определяющая долю концов цепей, связанных в узлах, и количество дефектных узлов, также влияет на дополнительные релаксационные процессы и переходы в стеклообразном состоянии.
Помимо молекулярной структуры аморфных полимеров заметное влияние на температуру и форму пиков механических потерь первичного (α) и вторичных (особенно β- и γ-) переходов в стеклообразном состоянии оказывает тип их надмолекулярной структуры и соответствующие структурные превращения при различных видах и условиях термообработки, а также при ориентационной вытяжке. На рис 4.4 приведены полученные высокочувствительным низкочастотным методом динамической механической спектрометрии температурные зависимости тангенса угла потерь в области β-релаксации для ПММА, подвергнутого закалке - быстрому охлаждению из высокоэластического в стеклообразное состояние (кривая 1) и отжигу при различных температурно-временных условиях (кривые 2-3):
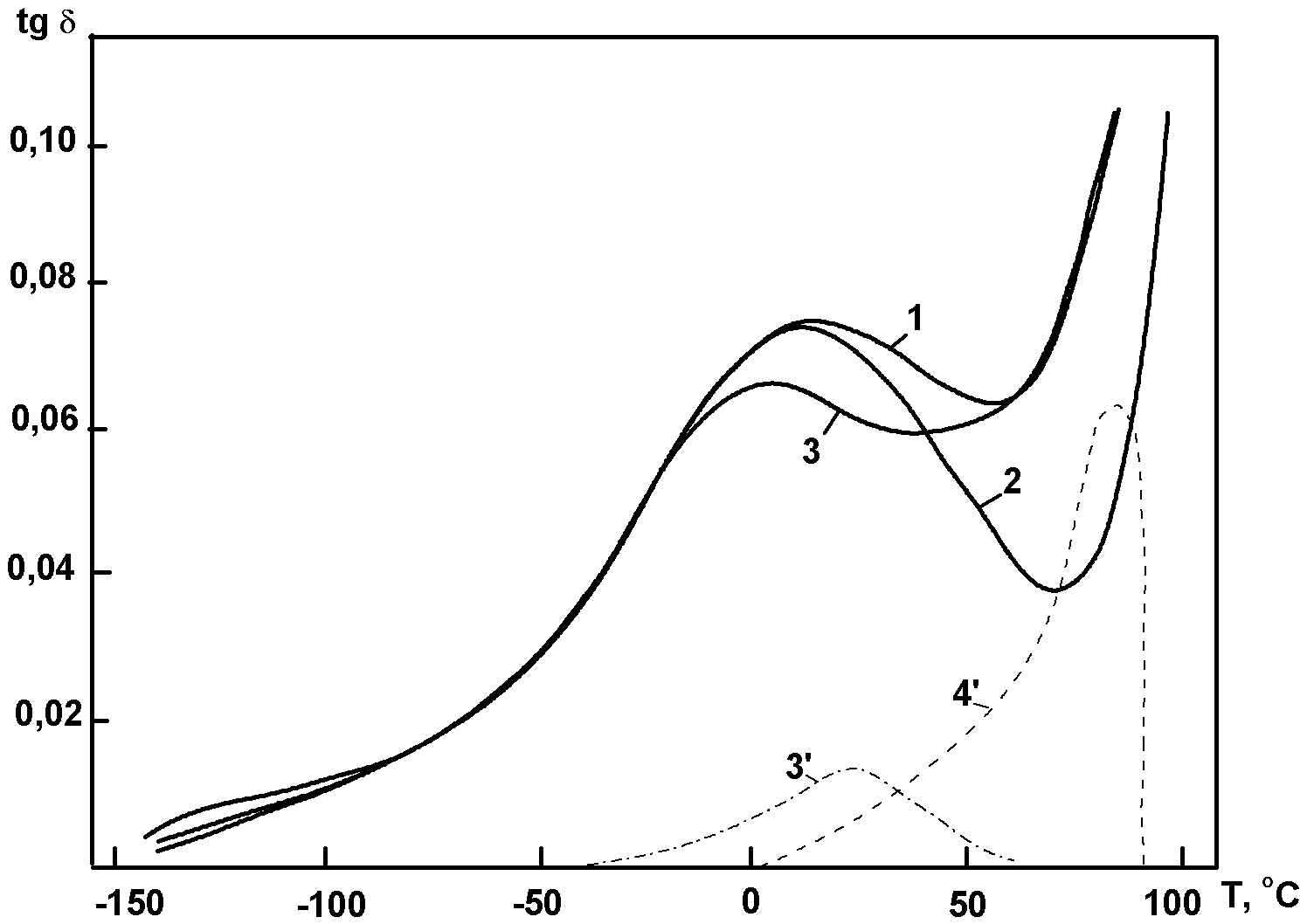
Рис 4.4. Температурные зависимости тангенса угла потерь в области β-релаксации при частоте 0,1 Гц для ПММА (температура стеклования 105 ОС), подвергнутого закалке - быстрому охлаждению от температуры, равной Тс + 30ОС (кривая 1), и отжигу при температуре 90ОС в течение 3,3.105 с (кривая 2) и при 23 ОС в течение 2,2.106 с (кривая 3). Пунктирные кривые 3΄ и 4΄ соответствуют разности между этими зависимостями для закаленного и отожженных при различных условиях образцов соответственно.
Из приведенного рисунка видно, что при высокой температуре отжига, близкой к температуре стеклования (кривая 2), высота и положение β-пика на температурной оси практически не изменяется, но его форма в правой части значительно более резко выражена, и разность Δtgδ между закаленным и отожженным образцами в этой области спектра велика. При более низкой температуре и большей длительности отжига изменяется и положение, и высота β-пика с резким уменьшением разности Δtgδ между закаленным и отожженным образцами в его правой части.
Определение динамических термомеханических спектров позволяет оценивать эффективность и механизм действия пластификаторов – малолетучих жидких растворителей, которые вводятся в аморфные полимеры для снижения их Тс, повышения эластичности и пластичности за счет повышения гибкости цепей. Пластификаторы обычно смещают перегиб на кривой модуля и пик показателя потерь в области стеклования в сторону более низких температур, понижая при этом высоту и расширяя пик показателя потерь, а также расширяют область (плато) высокоэластического состояния и уменьшают модуль в этой области (Рис. 4.5):
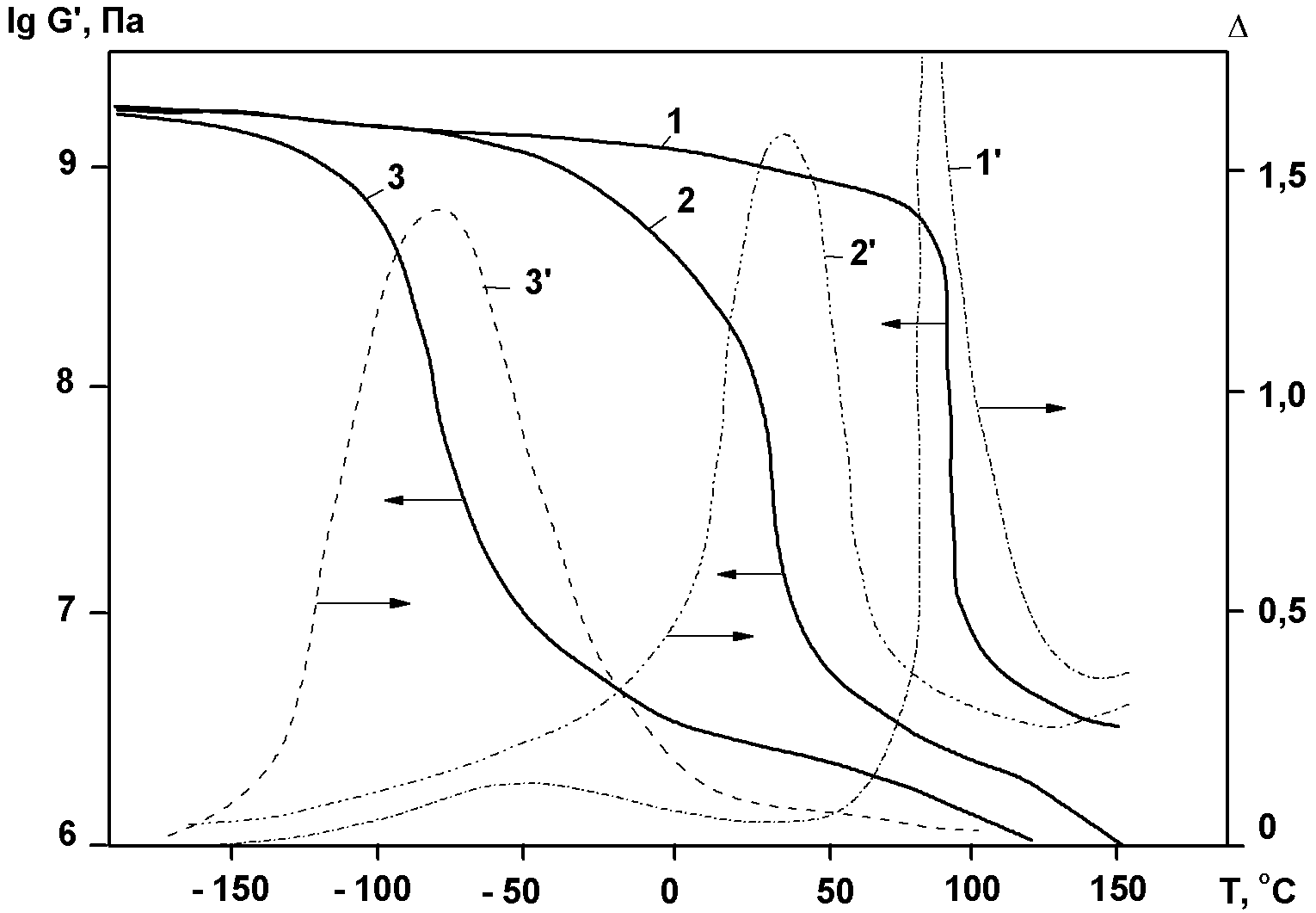
Рис.4.5.Динамические термомеханические кривые при частоте 1 Гц для поливинилхлорида (ПВХ), непластифицированного (1,1΄) и пластифицированного диэтилгексилсукцинатом в соотношении ПВХ/пластификатор 79/21 (2,2΄) , 51,8/41,2 (3,3΄): кривые 1-3 - G΄, 1΄-3΄ - декремент затухания Δ [Нильсен, с.116]
Эти эффекты сильно зависят от «качества» пластификатора как растворителя, т.е. типа его межмолекулярных связей с полимером. В некоторых случаях введение в аморфные полимеры растворимых жидкостей, способных образовывать сильные межмолекулярные связи с полимерами, сопровождается резким понижением пика γ-релаксации в стеклообразном состоянии и проявлением так называемого эффекта «антипластификации» - повышения модуля упругости в стеклообразном состоянии, хотя эффект понижения Тс, пропорциональный количеству веденной жидкости и ее Тс, при этом сохраняется (Рис.4.6).
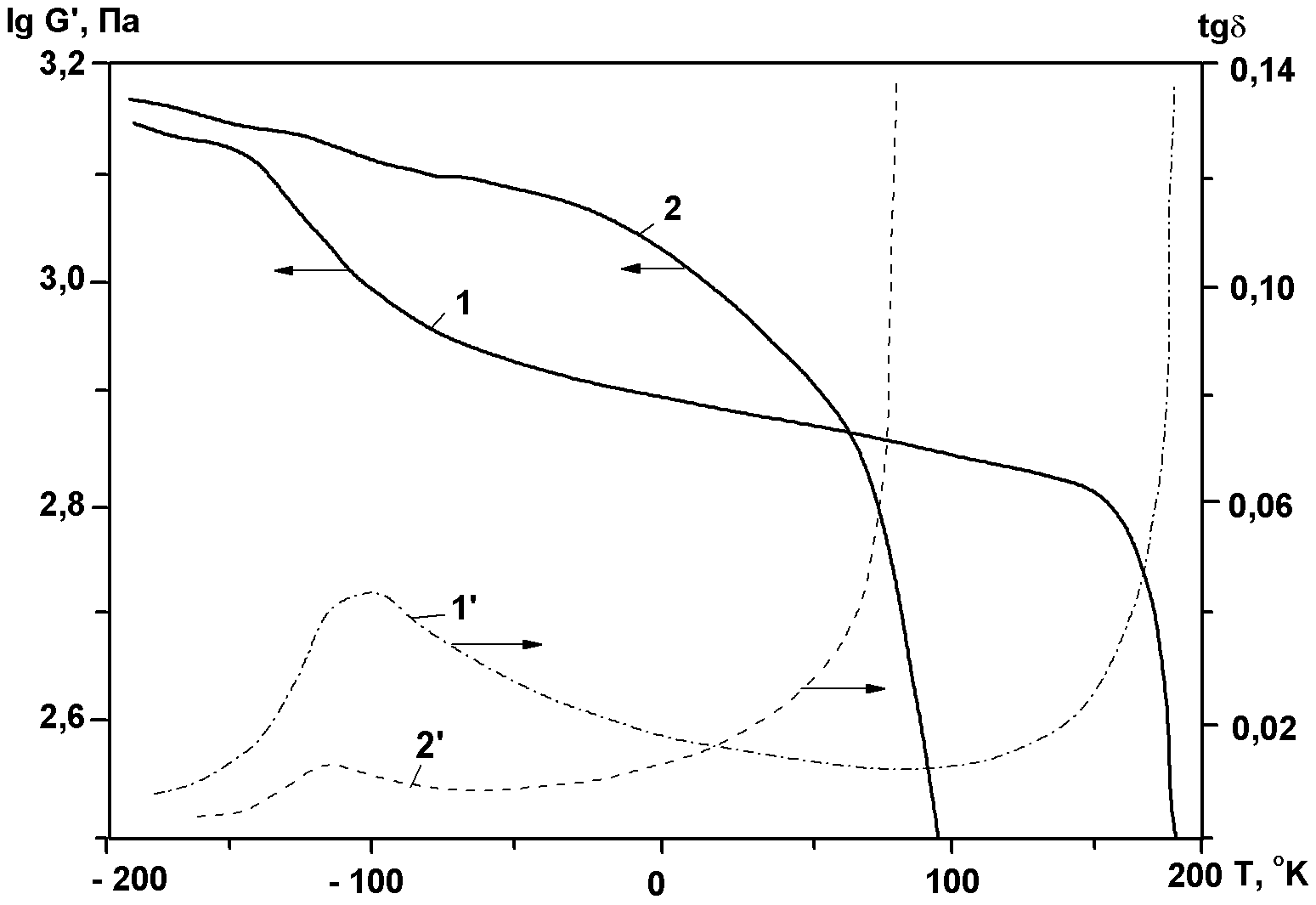
Рис.4.6. Динамические термомеханические кривые при частоте 1 Гц для полисульфона, непластифицированного (1,1΄) и пластифицированного 4,4΄-дихлордифенилсульфоном в количестве 30 масс.% (2,2΄): кривые 1-2 - G΄, 1΄-2΄ - tgδ [Нильсен, с.119].
Динамические термомеханические кривые очень чувствительны к сорбируемой полимерами воде и другим растворителям, оказывающим обычно пластифицирующий или антипластифицирующий эффект. Например, на рис.4.7 показано, что пик показателя потерь в области γ-релаксации в стеклообразном состоянии полисульфона заметно понижается с уменьшением количества влаги:
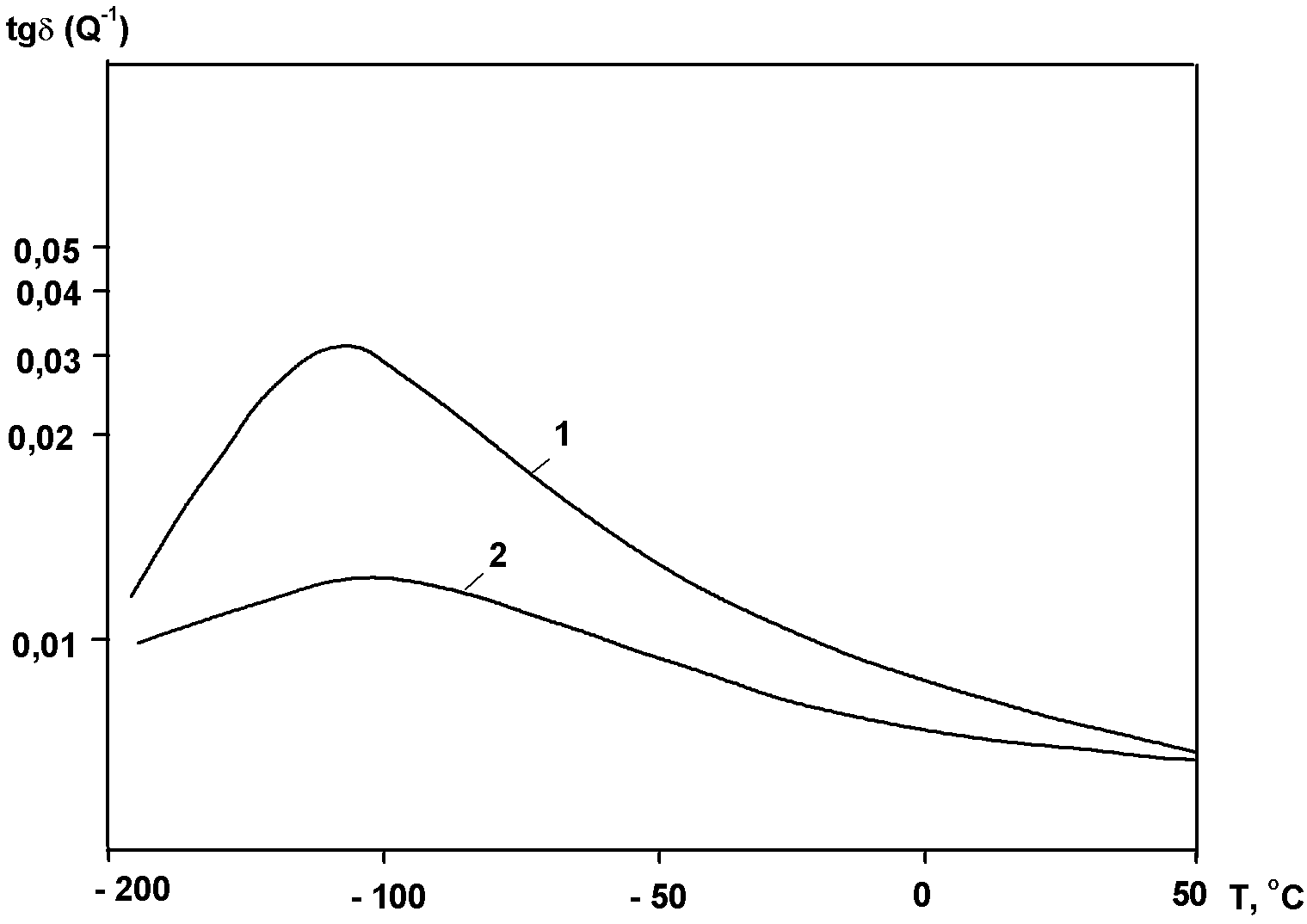
Рис.4.7..Динамические термомеханические кривые показателя потерь при частоте 1 Гц в области γ-релаксации для полисульфона, содержащего 0,31 масс.% (1) и 0,07 масс.% (2) воды [Polymer71,c.92, с.119].
Эти спектры также чувствительны к изменению типа связей в полимерах, например, к замене водородных связей между карбоксильными группами на ионные (Рис.4.8):
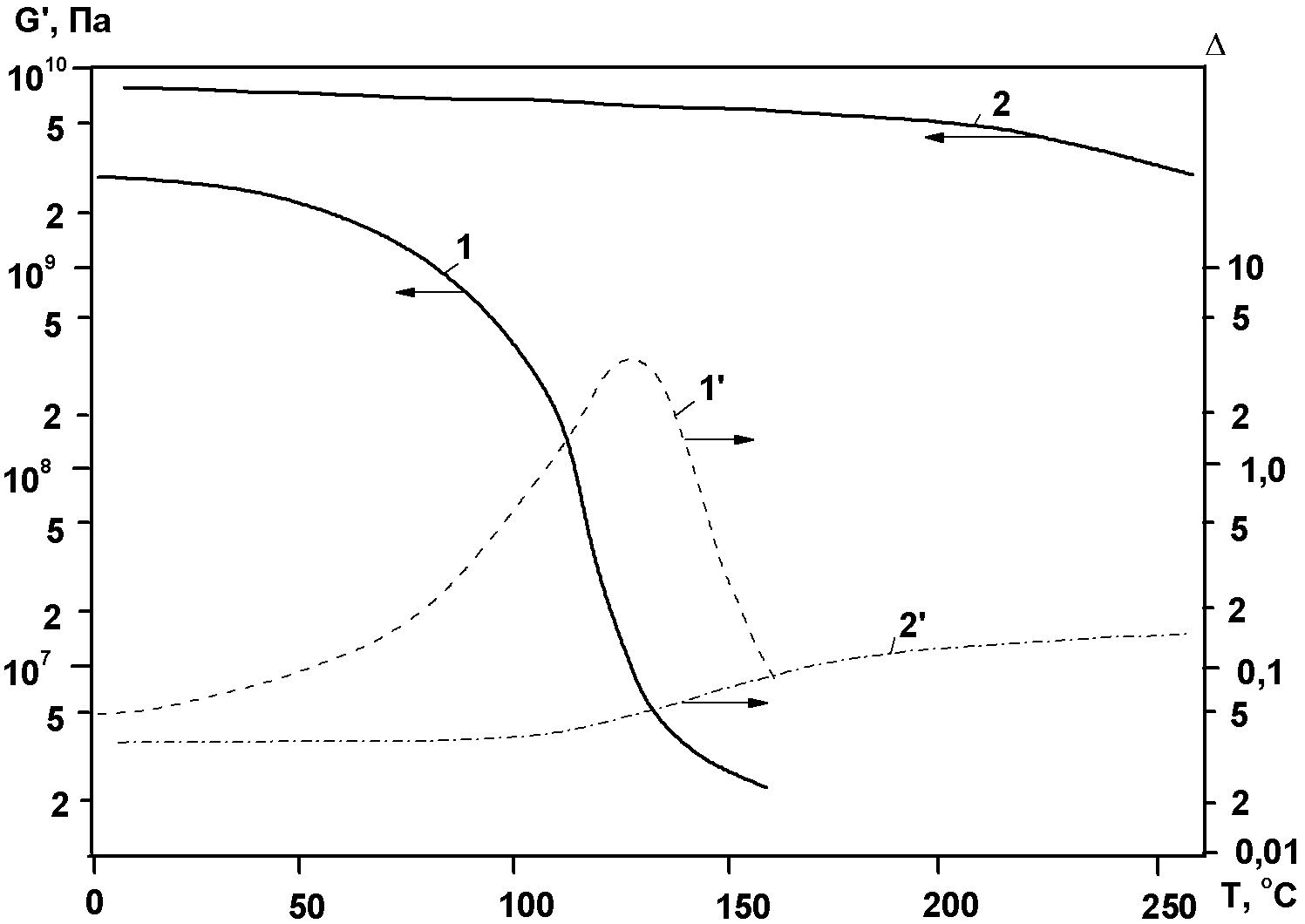
Рис.4.8..Динамические термомеханические кривые при частоте 1 Гц для сополимера акриловой кислоты (94%) и 2-этилгексилакрилата (6%) (1,1΄) и его соли цинка (2,2΄): кривые 1-2 - G΄, 1΄-2΄ - декремент затухания Δ [Нильсен, с.127].
Методы динамической механической спектрометрии широко применяются для исследования релаксационных процессов и переходов, сопровождающих реакции образования или химические превращения аморфных полимеров и полимеробразующих композиций. Особенно эффективно использование в этих целях устройств на основе прямых маятников, исследуемые образцы в которых представляют собой поддерживающие инерционную массу волокнистые структуры (плетеные нити, жгуты волокон или ткани), пропитанные исследуемым составом, помещенные в термокриокамеру с нейтральной или активной средой и совершающие малоамплитудные крутильные или изгибные колебания. При этом необходимо учитывать, что исследуются композиционные полимерные материалы, и поддерживающая (армирующая) нить влияет как на процессы химических и физических превращений полимерной матрицы, так и на характер деформирования образцов в целом.
Определение относительных изменений во времени параметров динамических вязко-упругих свойств образцов в таких методах (например, относительной жесткости и декремента затухания колебаний) в изотермических условиях с последующим определением динамических термомеханических кривых в широком температурном диапазоне после прохождения химической реакции до определенной глубины позволяет эффективно исследовать взаимосвязи химических и физических (фазовых и релаксационных) превращений полимеров и полимеробразующих композиций. Таким путем, например, получают обобщенные диаграммы реологических состояний и релаксационных переходов отверждаемых или сшиваемых реакционно-способных полимерных композиций в процессе их химических превращений при отсутствии фазовых превращений, так называемых хемореологических равновесных или кинетических диаграмм, соответственно, в зависимости от того, какой параметр контролируется – глубина или длительность отверждения.
На рис.4.9 приведены типичные кривые изменения относительной жесткости и декремента затухания колебаний в процессе изотермического отверждения по ступенчатому механизму эпоксиаминной композиции на основе диглицидилового эфира бисфенола А (ДГЭБА) и диаминодифенилметана (ДДМ) при эквимольном соотношении компонентов, претерпевающей переходы из вязко-текучего в высокоэластическое состояние (при Т›Тс композиции) в результате возникновении непрерывной полимерной сетки (в области гелеобразования) и из высокоэластического состояния в стеклообразное (в области стеклования) при достижении температуры стеклования композиции, равной температуре отверждения, а на рис.4.10 - обобщенная кинетическая диаграмма реологических состояний и релаксационных переходов этой композиции в координатах температура – время отверждения, полученная с помощью этих кривых:
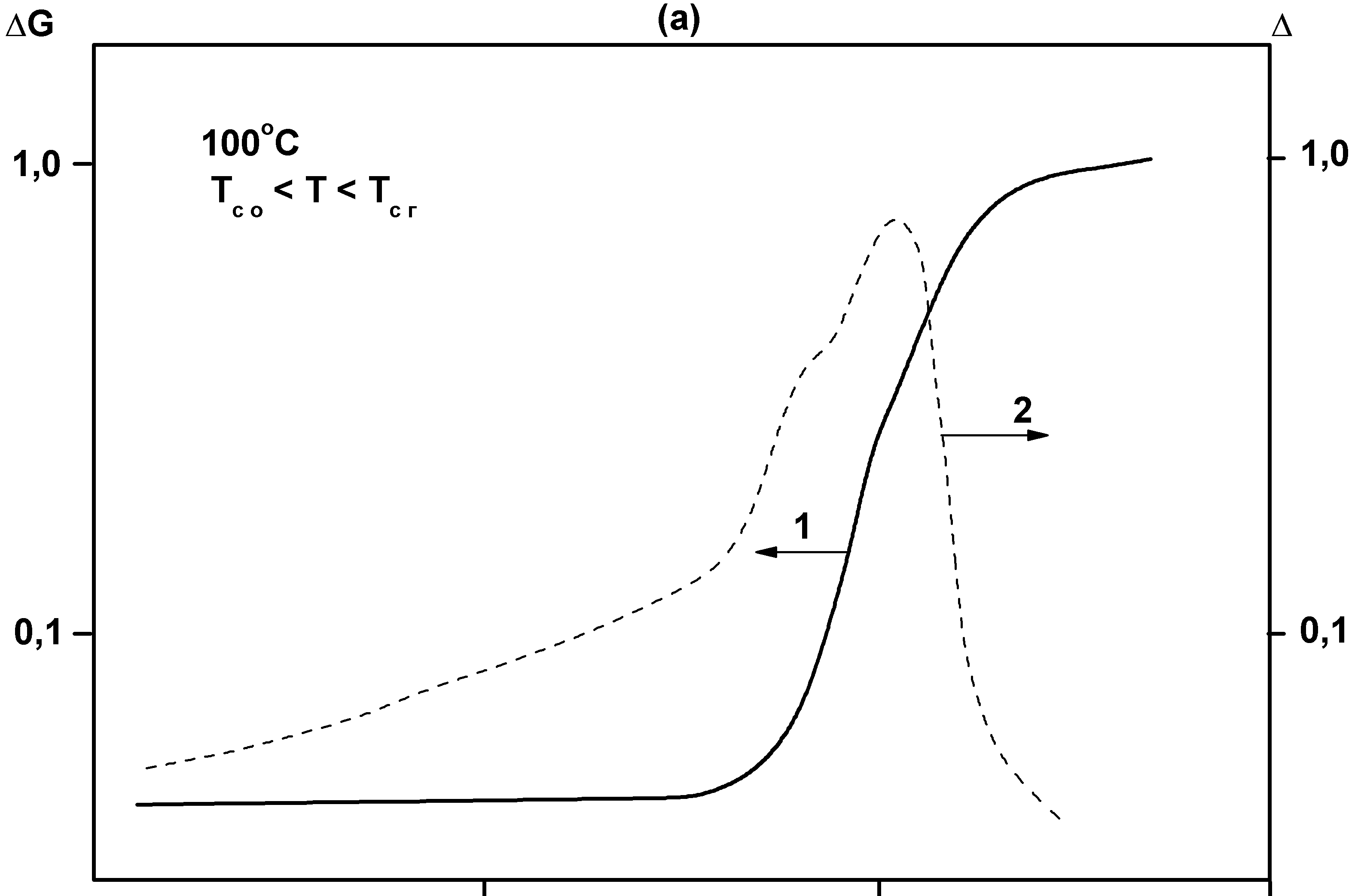
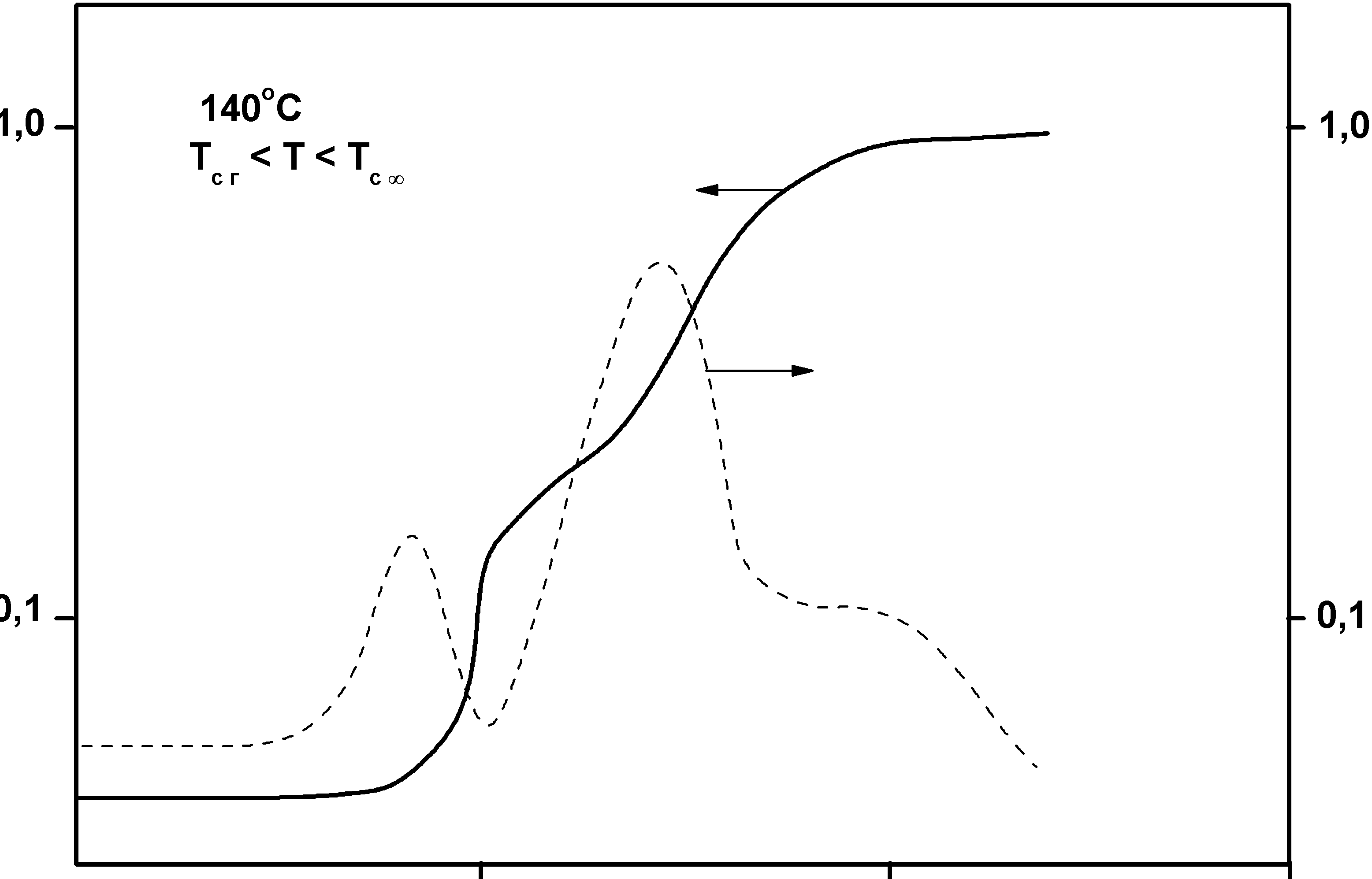
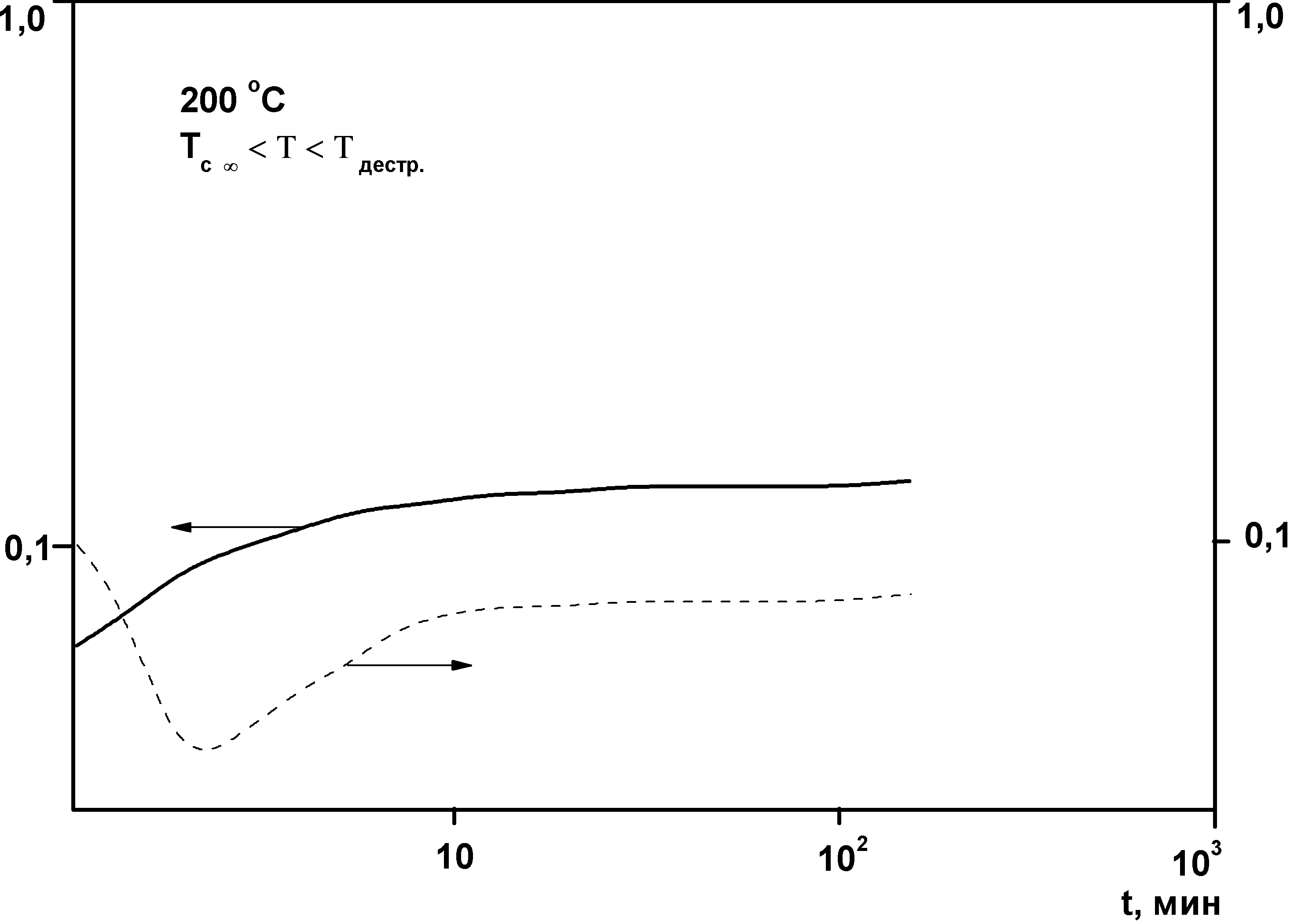
Рис. 4.9. Типичные кривые изменения относительной жесткости (1) и декремента затухания колебаний (2) в процессе изотермического отверждения эпоксиаминной композиции ДГЭБА-ДДМ в эквимольном соотношении при различной температуре: а) 100оС (Тс0‹Т‹ Тсг); б) 140 оС (Тсг ‹Т‹ Тс∞) и 200 оС (Тс∞ ‹Т‹ Тдестр)
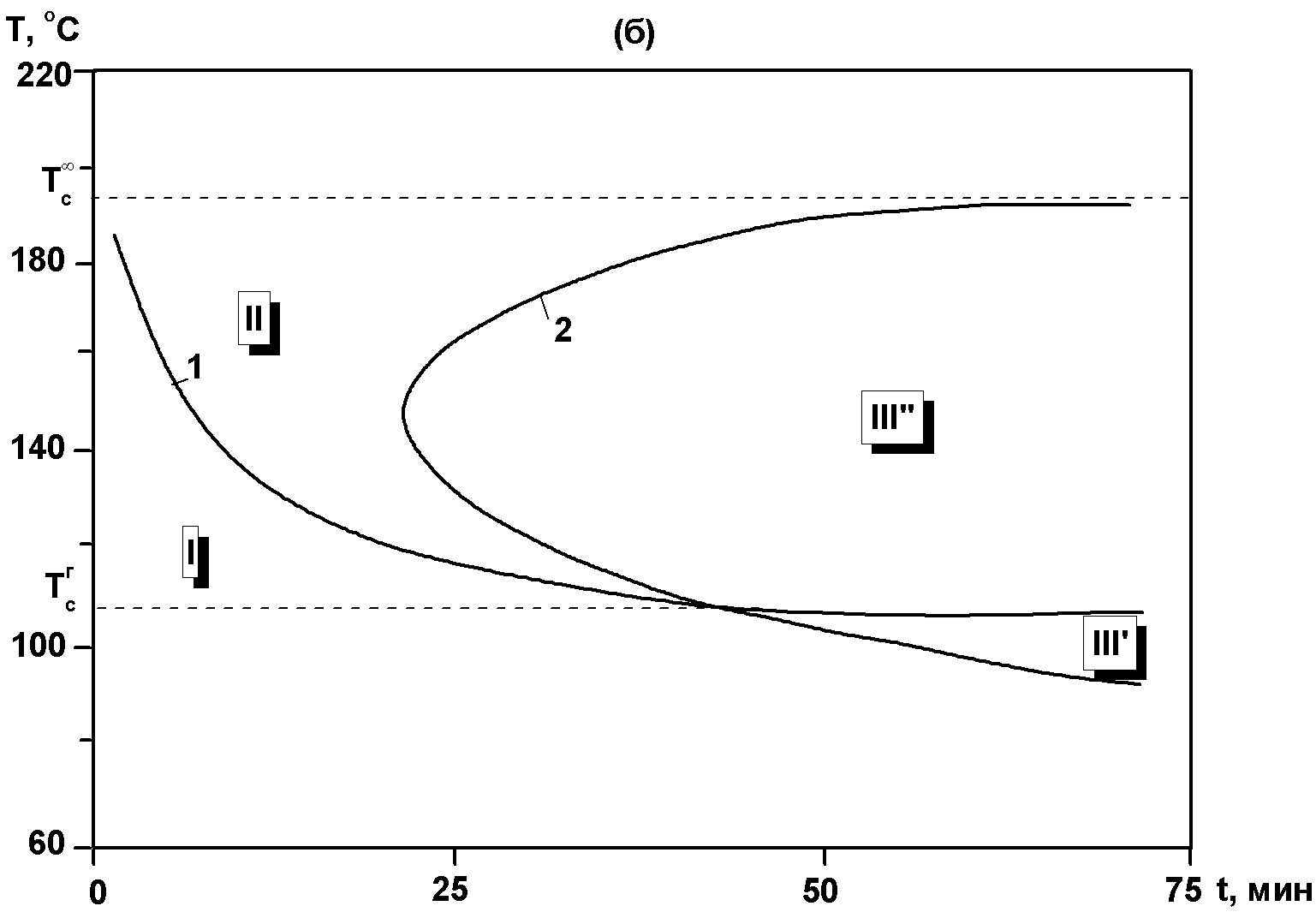
Рис.4.10. Обобщенная кинетическая диаграмма реологических состояний и релаксационных переходов композиции, аналогичной композиции на рис.4.9 в координатах температура – время отверждения (области состояний: I – вязко-текучего, II – высокоэластического, III΄ и III΄΄- стеклообразного до и после гелеобразования, соответственно, и линии переходов: 1 – гелеобразования, 2 – стеклования).
Эксперименты были проведены с помощью прямого крутильного маятника при частоте порядка 1 Гц с использованием образцов в виде плетеной стеклонити, пропитанной отверждаемой композицией и помещенной в термокриокамеру, через которую пропускался инертный газ. Приведенные данные показывают, что в зависимости от соотношения температуры отверждения и характерных температур стеклования данной композиции на различных стадиях ее отверждения (начальной Тс0, в области гелеобразования Тсг и на предельной стадии отверждения Тс∞) проявляются только пики показателя потерь и ступенчатое возрастание относительной жесткости, соответствующие только области стеклования (при Тс0‹Т‹ Тсг, рис.4.9а), областям гелеобразования и стеклования (при Тсг ‹Т‹ Тс∞, рис.4.9б) и только областям гелеобразования (при Тс∞ ‹Т‹ Тдестр, рис.4.9в). На обобщенной кинетической диаграмме, при условии, что Тс∞ ‹ Тдестр, выявляются все возможные реологические состояния и переходы таких композиций при различных температурах и на различных стадиях их отверждения.
Получение динамических термомеханических кривых при охлаждении до низких температур с заданной скоростью тех же образцов, что и при изотермическом отверждении, но после достижения ими заданной степени отверждения, позволяет находить корреляцию между степенью отверждения и релаксационными процессами и переходами, в первую очередь α- и β-процессами и переходами. На рис.4.11 приведены такие кривые при частоте порядка 1 Гц для эпоксиаминной композиции на основе диглицидилового эфира бисфенола А ДГЭБА и триметиленгликоль ди-п-аминобезоата (ТМАБ), полученные с помощью прямого крутильного маятника с плетеной стеклонитью, пропитанной отверждаемой композицией.
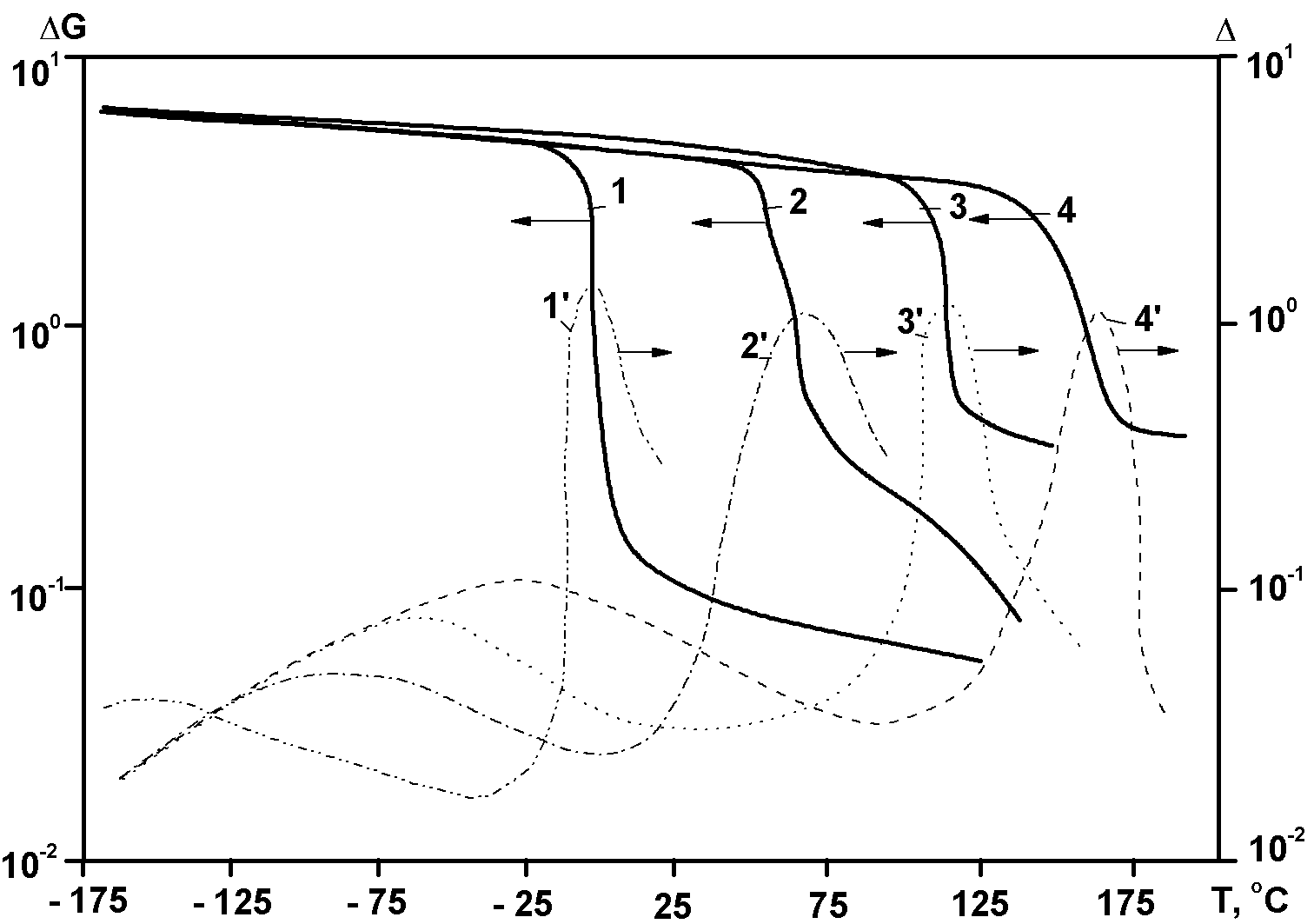
Рис. 4.11. Динамические термомеханические кривые при частоте порядка 1 Гц для эпоксиаминной композиции ДГЭБА–ТМАБ в эквимольном соотношении, полученные с помощью прямого крутильного маятника с плетеной стеклонитью, пропитанной отверждаемой композицией, после отверждения до различной степени: 0 (1,1΄), 0,64 (2,2΄), 0,86 (3,3΄) и 0,96 (4,4΄)при охлаждении от температуры отверждения.
Наблюдается четкая корреляция между степенью отверждения (определена независимо методом дифференциальной сканирующей калориметрии, ДСК) и температурами α- и β-переходов, причем характер зависимостей температур переходов, особенно β-перехода, от степени отверждения резко изменяются в области гелеобразования, в которой происходит переход от конечной структуры макромолекул к непрерывной полимерной сетке (Рис. 4.12). Полученные при этом корреляционные кривые в сочетании с линией гелеобразования в координатах температура–степень отверждения являются равновесными диаграммами хемореологических состояний и превращений отверждающихся композиций.
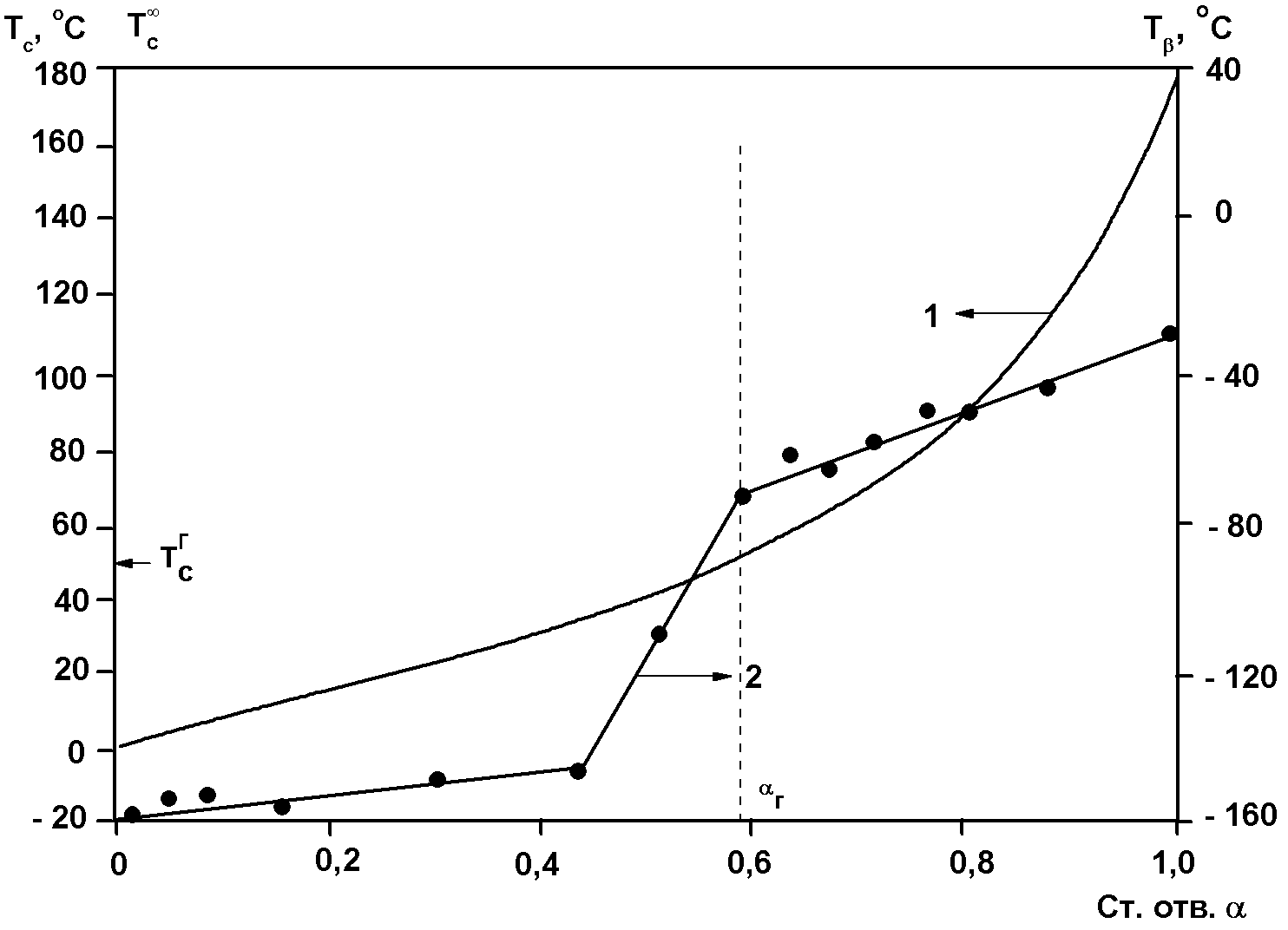
Рис.4.12. Корреляция между температурами стеклования (1) и β-перехода (2), определенными по динамическим термомеханическим кривым при частоте порядка 1 Гц, и степенью отверждения, определенной методом ДСК, для эпоксиаминной композиции ДГЭБА–ТМАБ при эквимольном соотношении компонентов (линия гелеобразования показана пунктиром).
Динамическая термомеханическая спектрометрия является также эффективным методом исследования гетерофазных полимеров и полимерных материалов (ГПМ): аморфно-, или частично-кристаллических полимеров и аморфных некристаллизующихся смесей и сплавов полимеров, блок и привитых сополимеров и полимеробразующих композиций, а также композиционных полимерных материалов (дисперсно-наполненных, армированных и вспененных КПМ) на основе как однофазных аморфных, так и гетерофазных ПМ матриц.
Наиболее простыми и сравнительно легко поддающимися интерпретации динамическими термомеханическими спектрами обладают однокомпонентные кристаллизующиеся полимеры и двухкомпонентные некристаллизующиеся полимерные или полимеробразующие композиции, претерпевающие фазовые превращения – частичную кристаллизацию и аморфное разделение, соответственно, с образованием двухфазных аморфно-кристаллических и двухфазных аморфных ПМ. Ниже основное внимание уделено анализу динамических механических спектров именно таких ГПМ. Интерпретация механических спектров сложных многокомпонентных и многофазных, в том числе кристаллизующихся и мезофазных полимерных материалов, базируется на анализе более простых двухфазных ГПМ. Механические спектры гетерофазных КПМ в решающей степени определяются полимерной или полимеробразующей фазой и ее межфазными областями, так как в не полимерных фазах релаксационные процессы практически не проявляются.
Динамические термомеханические спектры аморфно-кристаллических полимеров обычно содержат широкие области ступенчатого изменения динамического модуля и пики или плечи на кривых показателей механических потерь, соответствующие релаксационным процессам и переходам, протекающим в кристаллических и аморфных областях. При этом наиболее крпномасштабные релаксационные процессы, протекающие в кристаллических областях и связанные с подвижностью дефектов (конформационных аномалий в цепях), обозначаются как α-процессы, а соответствующие им релаксационные переходы (пики потерь) - как α-переходы. Таких процессов может быть несколько в зависимости от типа дефектов Релаксационные процессы и переходы, связанные с крупномасштабной (кооперативной) формой сегментальной подвижности в межламелярных и межсферолитных аморфных областях аморфно-кристаллических полимеров, т.е. с процессами стеклования в этих областях, обозначаются как β- и γ-процессы, переходы и пики потерь соответственно. Эти обозначения не следует путать с аналогично обозначаемыми релаксационными процессами и переходами в однофазных аморфных (некристаллизующихся) полимерах, связанными с крупно- и мелкомасштабными формами сегментального движения в них.
На рис.4.13 схематически представлены динамические термомеханические спектры аморфно-кристаллического полимера с высокой и низкой степенью кристалличности, а на рис. 4.14а,б – конкретные примеры таких спектров для полиэтилена высокой плотности (ПЭВП) и стереорегулярного полипропилена (ПП) при частоте 1 Гц в широком интервале температур:
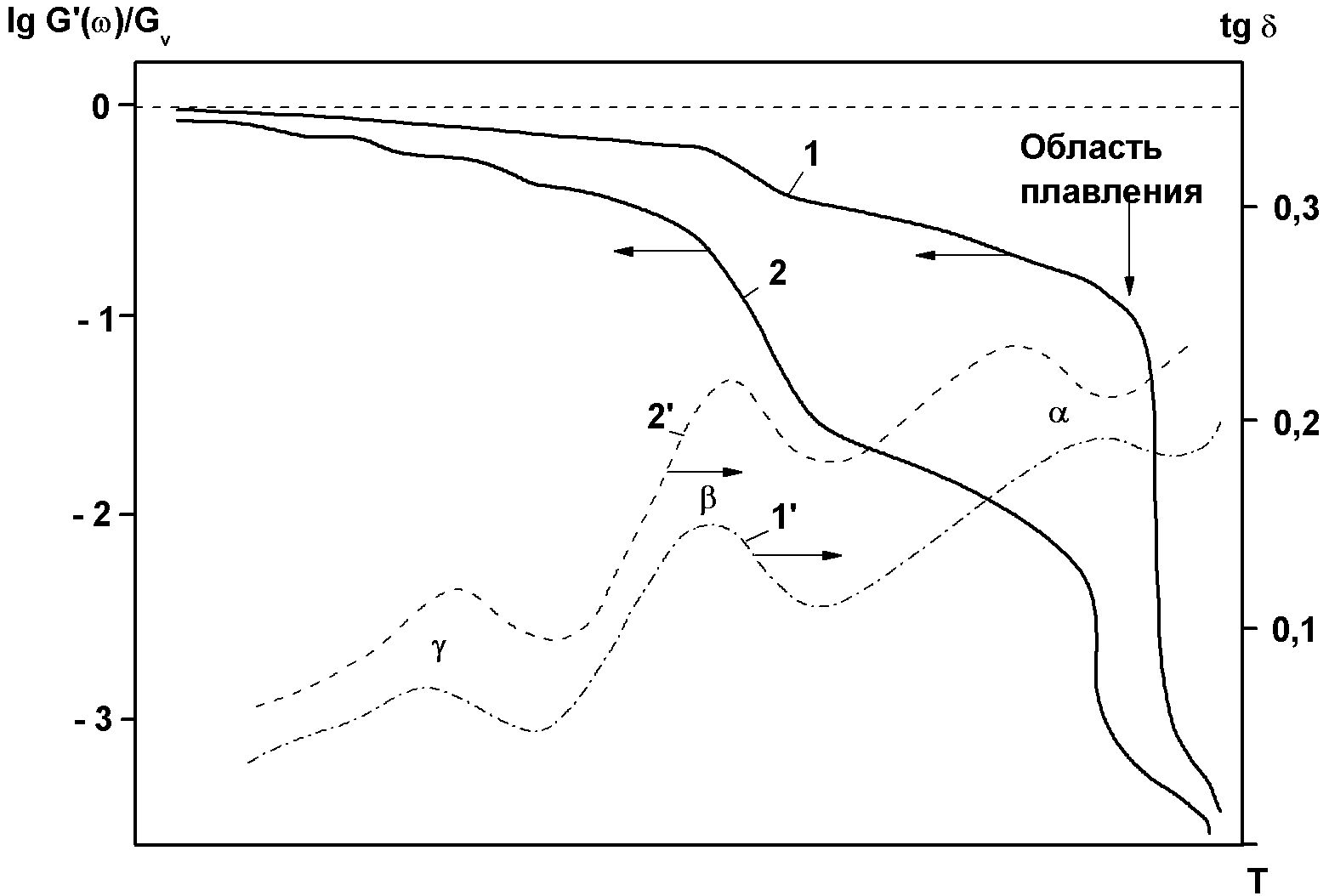
Рис.4.13. Схематическое изображение динамических термомеханических кривых аморфно-кристаллического полимера с высокой (1,1΄) и низкой (2,2΄) степенью кристалличности: области основной релаксации в кристаллической фазе (α), стеклования аморфной фазы (β) и дополнительной релаксации в аморфной фазе (γ).
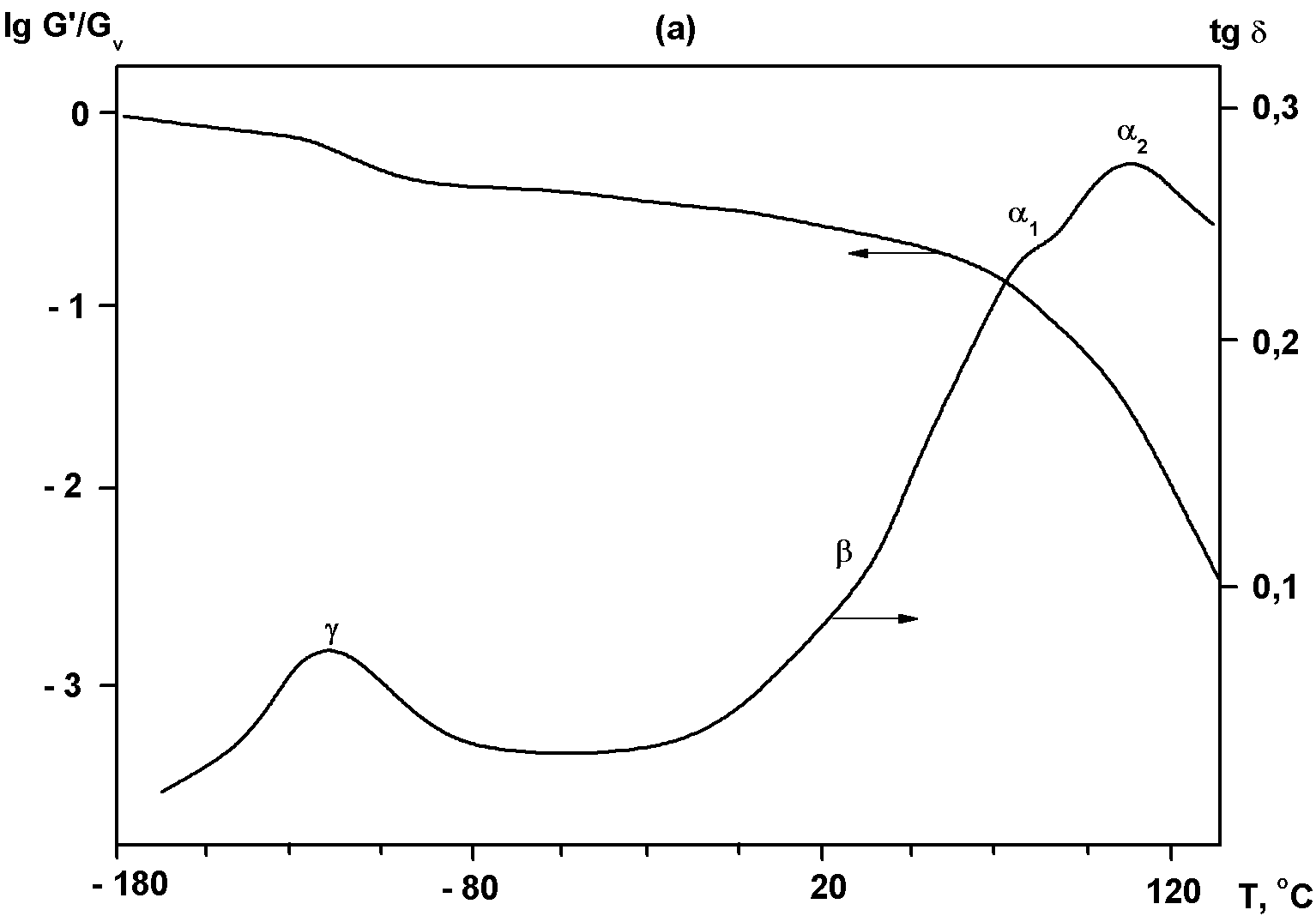
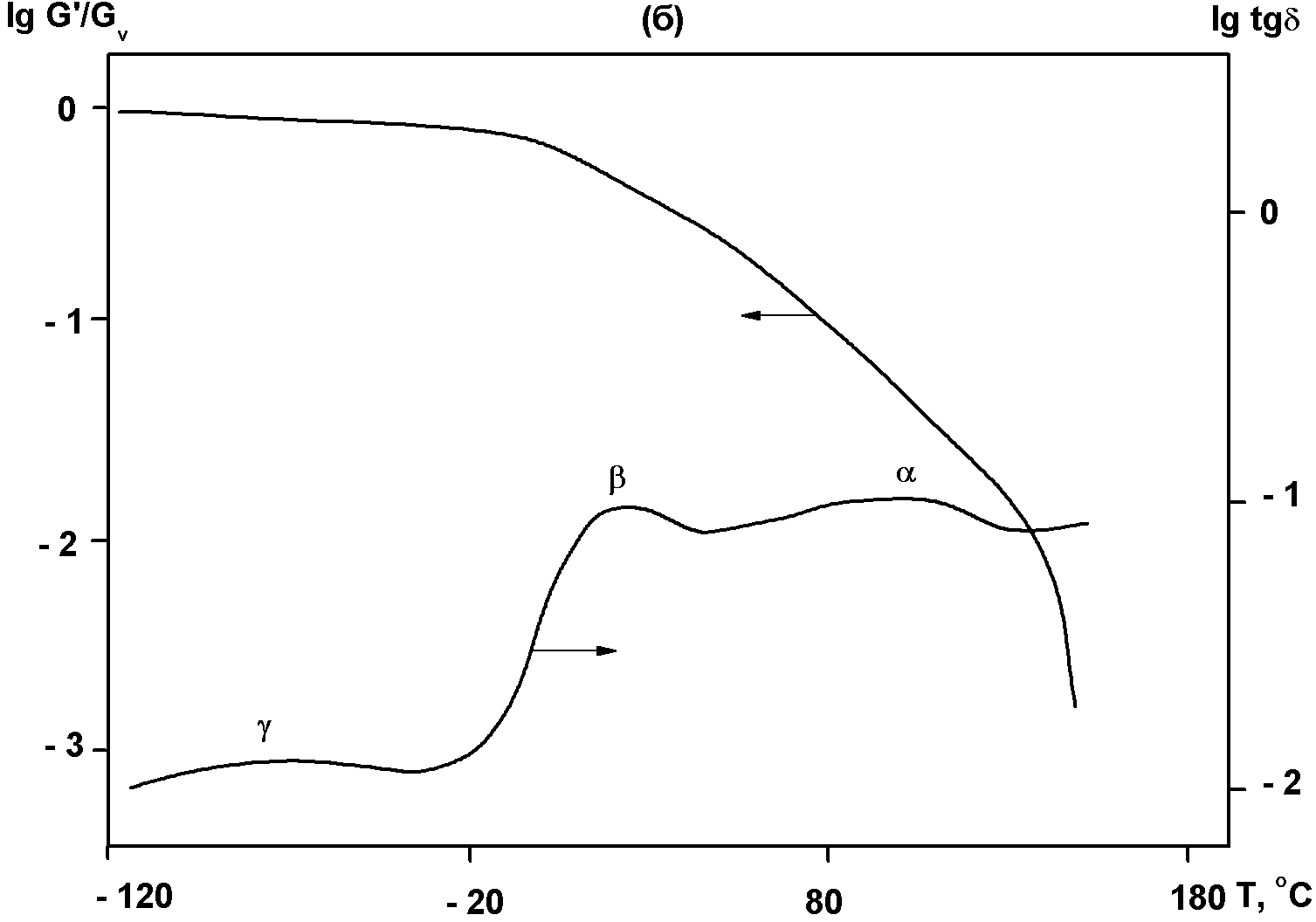
Рис.4.14. Динамические термомеханические кривые аморфно-кристаллических полимеров с высокой степенью кристалличности при частоте 1 Гц: а) ПЭВП; б) ПП: области релаксации в кристаллической (α) и в аморфной (β и γ) фазах.
На этих спектрах видны три наиболее важных релаксационных процесса (пика потерь) – α, β и γ. Высокотемпературный и наиболее крупномасштабный α–пик, соответствующий максимуму tgδ порядка 0,25 и относящийся к кристаллическим областям, охватывает широкую температурную область (от 40 до 100 оС при частоте 1 Гц) и может разлагаться, как например в случае ПЭВП, на два пика (α1 и α2), которые имеют одинаковую природу, но соответствуют разной толщине ламелей: α1- более тонким, α2 – более толстым. Предполагается, что второй по величине β-пик соответствует стеклованию межламелярных аморфных областей, а γ-пик относится к главному релаксационному переходу (стеклованию) в межсферолитных аморфных областях. С увеличением степени кристалличности аморфно-кристаллических полимеров относительная высота всех пиков уменьшается, а в интервале температуры между Тпл и Тβ при этом резко повышается уровень динамического модуля упругости.
Расчеты динамических термомеханических спектров с учетом свойств аморфных и кристаллических областей и степени кристалличности показывают хорошее согласие с экспериментально полученными данными для гибкоцепных стереорегулярных. аморфно-кристаллических полимеров, в том числе полиэтилена высокой и низкой плотности, полипропилена, полиэтилентерефталат, алифатических полиамидов, поливинилиденфторида и других.
На рис.4.15 приведен в качестве примера частотные изотермические динамические механические спектры ПЭВП в интервале малых частот при двух температурах, лежащих в области между Тα и Т β.
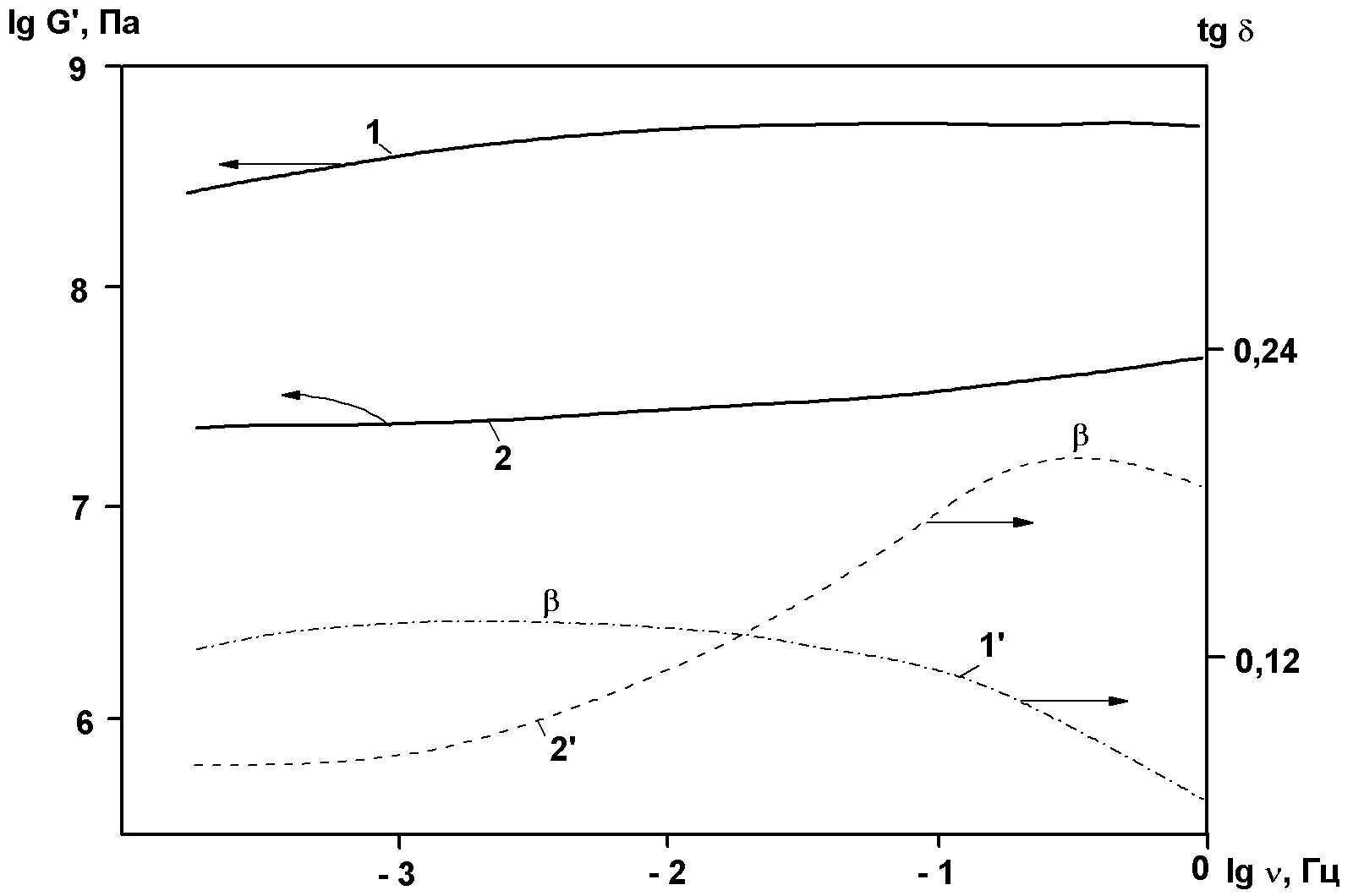
Рис. 4.15. Частотные зависимости динамических механических свойств (lgG΄ - кривые 1,2 и tgδ – кривые 1΄,2΄) ПЭВП при температуре 30оС (1, 1΄) и 110 оС (2, 2΄).
Приведенные кривые показывают, что при повышении температуры, как и следовало ожидать в соответствие с принципом температурно-частотной аналогии, пик потерь, относящийся вероятнее всего к β-процессу, смещается в сторону более высоких частот с уменьшением его ширины и увеличением высоты. При этом очевидна значительно более низкая разрешающая способность частотных изотермических спектров по сравнению с изохронными температурными, при том, что варьирование частоты в динамических механических методах представляет значительно большие трудности, чем температуры.
Эффекты отжига (физического старения) и закалки проявляются в механических спектрах аморфно-кристаллических полимеров через соответствующее изменение степени кристалличности и размеров кристаллитов и обычно ответственны за несовпадение спектров, полученных при нагревании и охлаждении или при различной скорости изменения температуры. Ориентационные эффекты проявляются в изменении формы кристаллических образований и появлении анизотропии структуры и свойств полимера.
Смеси или сплавы аморфно-кристаллических полимеров имеют значительно более сложные механические спектры, чем отдельные ограниченно совместимые компоненты (Рис.4.16).
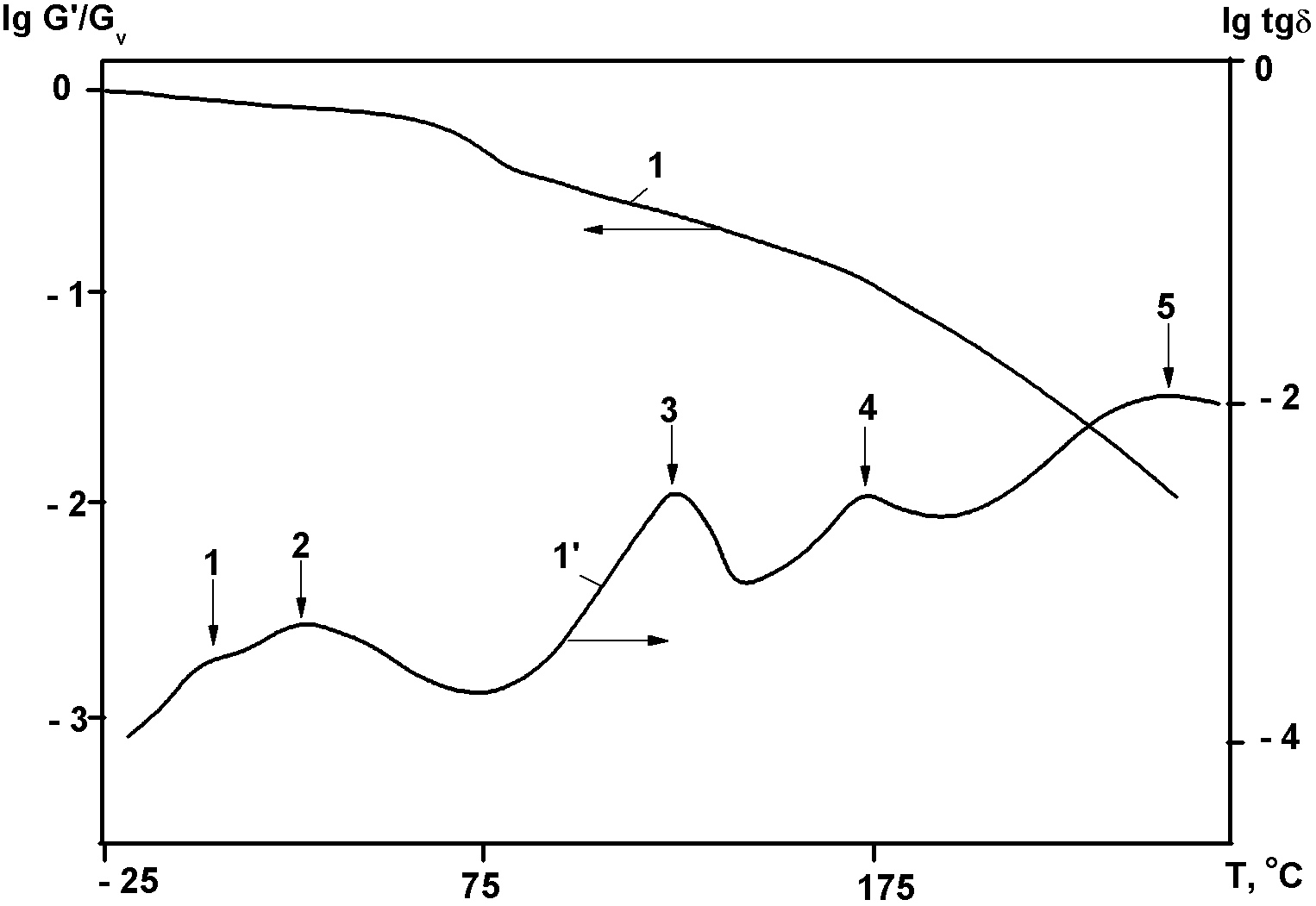
Рис.4.16. Температурные зависимости динамического модуля упругости при сдвиге lgG΄/G0 (1), где G0- мгновенный модуль, и показателя потерь lgtgδ(1΄) при частоте 1 Гц для смеси ПЭВП-ПП в соотношении 1:1. Области пиков 1,2 относятся к аморфной фазе ПЭ, 3 – к межфазной области взаимного растворения ПЭ-ПП, 4 – к аморфной фазе ПП и 5 – к кристаллическим фазам компонентов.
При этом, помимо релаксационных процессов, характерных для аморфных и кристаллических областей исходных полимеров, которые накладываются друг на друга, проявляются также процессы, характерные для межфазных областей взаимной растворимости компонентов.
Методы динамической механической спектрометрии могут эффективно применяться для исследования фазовых и релаксационных переходов, сопровождающих взаимодействие полимеров, в том числе аморфно-кристаллических, с низкомолекулярными веществами, в частности при сорбции и десорбции паров растворителей. При этом, по аналогии с исследованиями взаимосвязи химических и физических превращений в реакционноспособных полимерообразующих композициях, особенно эффективно использование устройств, совмещающих сорбционную установку и прямой маятник, исследуемые образцы в котором совершают малоамплитудные крутильные или изгибные колебания и представляют собой поддерживающие инерционную массу волокнистые структуры (плетеные нити, жгуты волокон или ткани), пропитанные исследуемым составом и помещенные в термокриокамеру с заданной средой (см. раздел 3). Комбинирование при этом кинетических кривых и изотерм сорбции или десорбции растворителя при различной его активности с аналогичными кривыми изменения динамических вязко-упругих свойств (относительной жесткости и декремента затухания) позволяет получать равновесные или кинетические диаграммы фазовых и релаксационных переходов и состояний исследуемых систем в широком интервале температур и активностей или концентраций паров растворителя. На рис. 4.17 в качестве примера приведены кривые относительного изменения вязко-упругих свойств в системе кристаллизующийся поливиниловый спирт-вода в зависимости от объемной доли сорбированной воды (а) и обобщенная диаграмма фазовых и релаксационных переходов и состояний такой системы в координатах температура-состав (б):
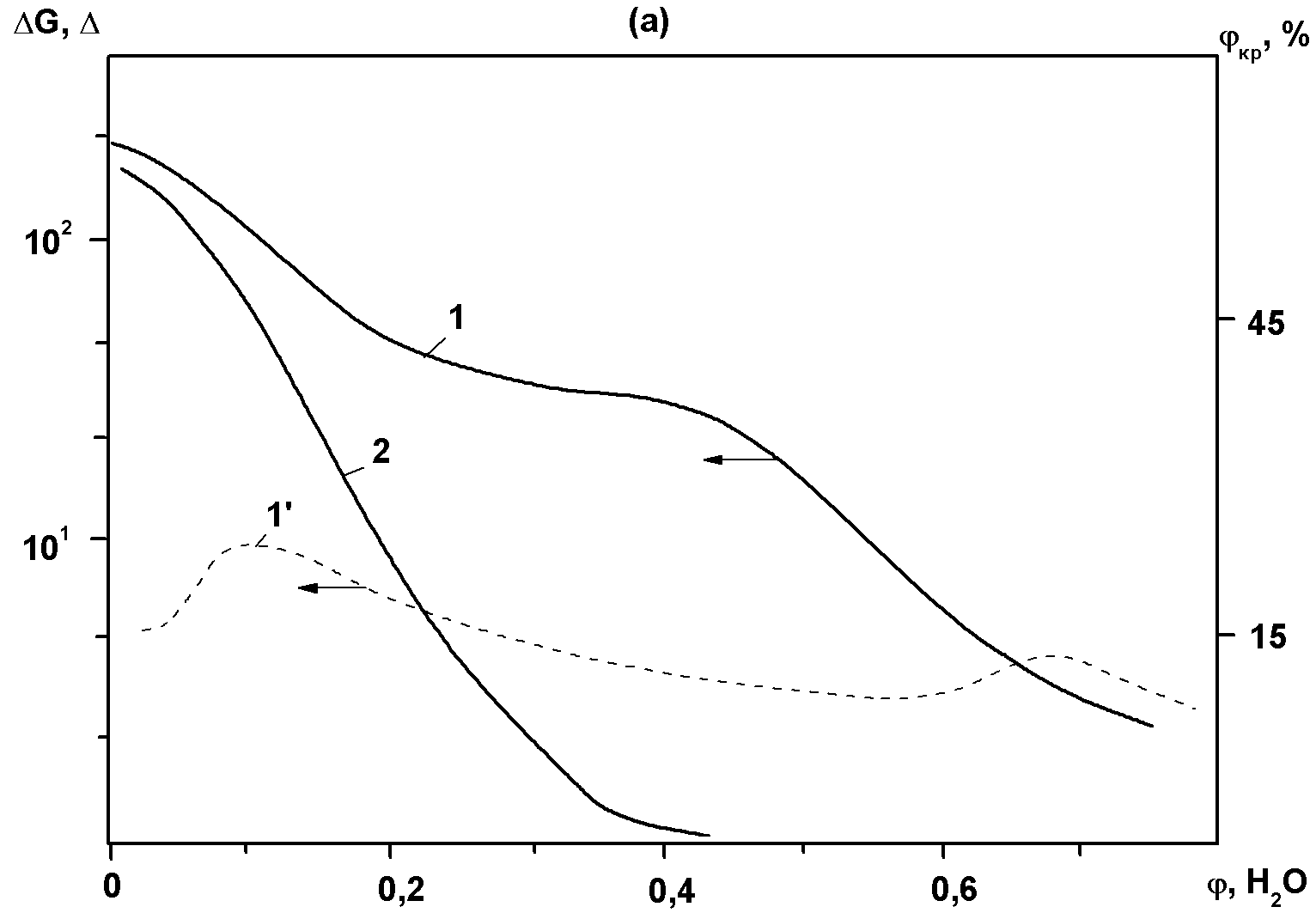

Рис.4.17. Изотермы (при 300С) относительного изменения вязко-упругих свойств (относительной жесткости ΔG, кривая 1, декремента затухания Δ, кривая 1΄), определенных методом крутильного маятника с образцом в виде стеклонити, пропитанной исследуемым полимером, и степени кристалличности (кривая 2), определенной методом рентгеноструктурного анализа, поливинилового спирта, в зависимости от объемной доли воды при десорбции ее паров из равновесно набухшего полимера (а) и обобщенная диаграмма фазовых и релаксационных переходов и состояний такой системы в координатах температура-состав: линии переходов: 1- студнеобразования за счет микро-кристаллизации, 2- макрокристаллизации, 3 – стеклования, 4 – β-перехода в стеклообразном состоянии аморфных областей, 5 – плавления несвязанной воды; области состояний: I - аморфного эластического, II – аморфно-кристаллического с эластичной аморфной фазой, III - аморфно-кристаллического с стеклообразной аморфной фазой (б) [ ВМС.Рис.5,7].
Динамическая термомеханическая спектрометрия является также очень эффективным методом исследования релаксационных процессов и переходов в отдельных фазах и межфазных областях аморфных двухфазных ПМ. На примере динамических термомеханических спектров тройного блок-сополимера полистирол-полибутадиен-полистирол (ПС-ПБ-ПС), пленочные образцы которого формировались из растворов в различных растворителях (Рис.4.18) показана высокая чувствительность динамической механической спектрометрии к фазовой структуре и составу фаз гетерогенных полимерных смесей. На приведенных спектрах пики механических потерь в области 100ОС соответствуют фазе, обогащенной блоками ПС, а в области -70 ОС - ПБ.
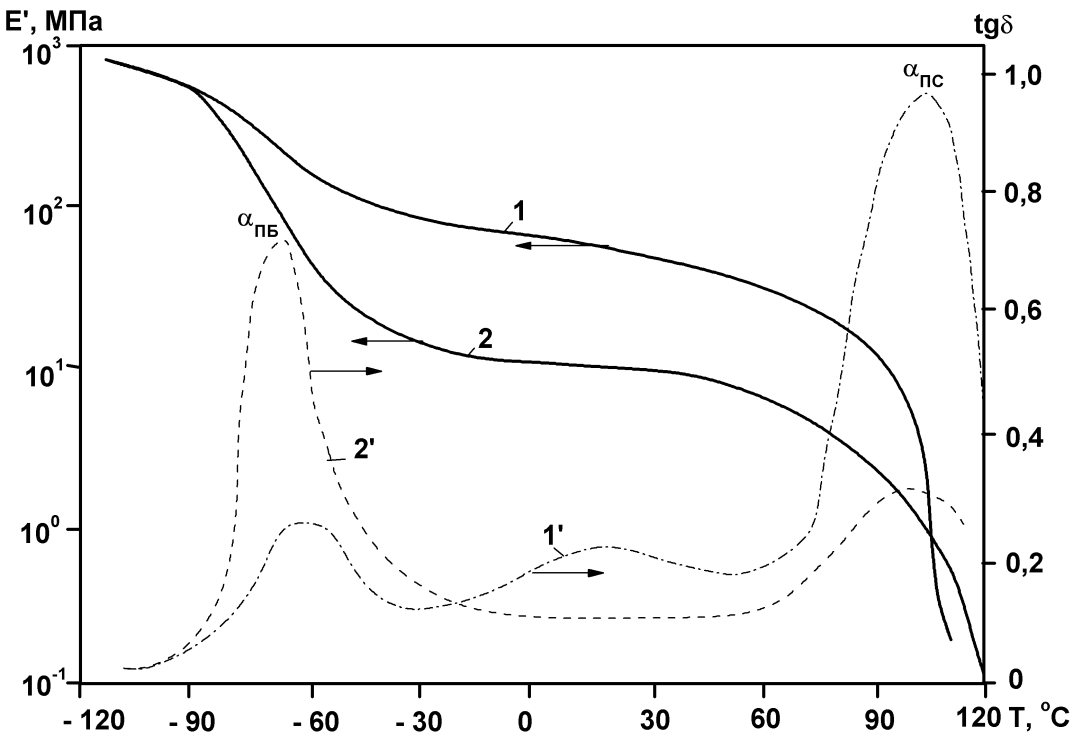
Рис.4.18. Динамические термомеханические кривые в координатах Е΄ (1,2) и tgδ (1΄,2΄) при частоте 1 Гц трехблочного сополимера ПС-ПБ-ПС с содержанием блоков ПС 30 мас.% и их молекулярной массой Mw =1.5.104, полученного из растворителя, «хорошего» для блоков ПС и «плохого» для блоков ПБ (метилэтилкетона) (1,1΄) и «хорошего» для блоков ПБ и «плохого» - для блоков ПС (четыреххлористого углерода) (2,2΄).
Видно, что в случае образцов, полученных из раствора в метилэтилкетоне, являющегося термодинамически «хорошим» растворителем для блоков ПС и «плохим» - для блоков ПБ, непрерывную фазу образуют преимущественно блоки ПС, а дисперсную – блоки ПБ, что проявляется в высоком высокотемпературном пике и низком низкотемпературном, а также в высоких значениях модуля упругости в области между этими переходами (см. кривые 1,1΄ на рис. 4.18). Наоборот, в случае образцов, полученных из раствора в четыреххлористом углероде, являющегося термодинамически «хорошим» растворителем для блоков ПБ и «плохим» - для блоков ПС, непрерывную фазу образуют преимущественно блоки ПБ, а дисперсную – блоки ПС, что проявляется в высоком низкотемпературном пике и низком высокотемпературном, а также в низких значениях модуля упругости в области между этими переходами (см. кривые 2,2΄ на рис. 4.18). Появление пика потерь на кривой 1΄ вблизи комнатной температуры связывается с образованием метастабильной фазы с взаимным растворением блоков ПС и ПБ.
При использовании методов расчета динамических механических свойств гетерофазных полимерных систем по свойствам фаз и их объемному соотношению с учетом характера взаимного распределения фаз, или фазовой морфологии с использованием экспериментально определенных соответствующим способом динамических термомеханических спектров отдельных компонентов и их смесей, можно получить более глубокую информацию о составе смесей, их фазовой морфологии и даже о составе межфазных слоев. Так, на рис.4.19 б,в приведены рассчитанные температурные динамические механические спектры матричных дисперсий двух некристаллизующихся ограниченно совместимых полимеров с резко различной температурой стеклования Тс (полиметилметакрилата, ПММА, с Тс выше комнатной температуры и полибутилакрилата, ПБА, с Тс ниже комнатной температуры) по экспериментально определенным при частоте 110 Гц их спектрам, приведенным на рис. 4.19а, при допущениях, что матрица смеси состоит из стеклообразного полимера, ПММА, а дисперсная фаза – из эластичного ПБА (рис. 4.19б) и наоборот – непрерывную фазу образует эластичный полимер, ПБА, а дисперсную – стеклообразный ПММА (рис. 4.1в). Объемная доля дисперсной фазы в смесях принималась равной 0,25 и 0,75 (кривые 3,3΄ и 4,4΄ соответственно) [Дики, с.160-161]:
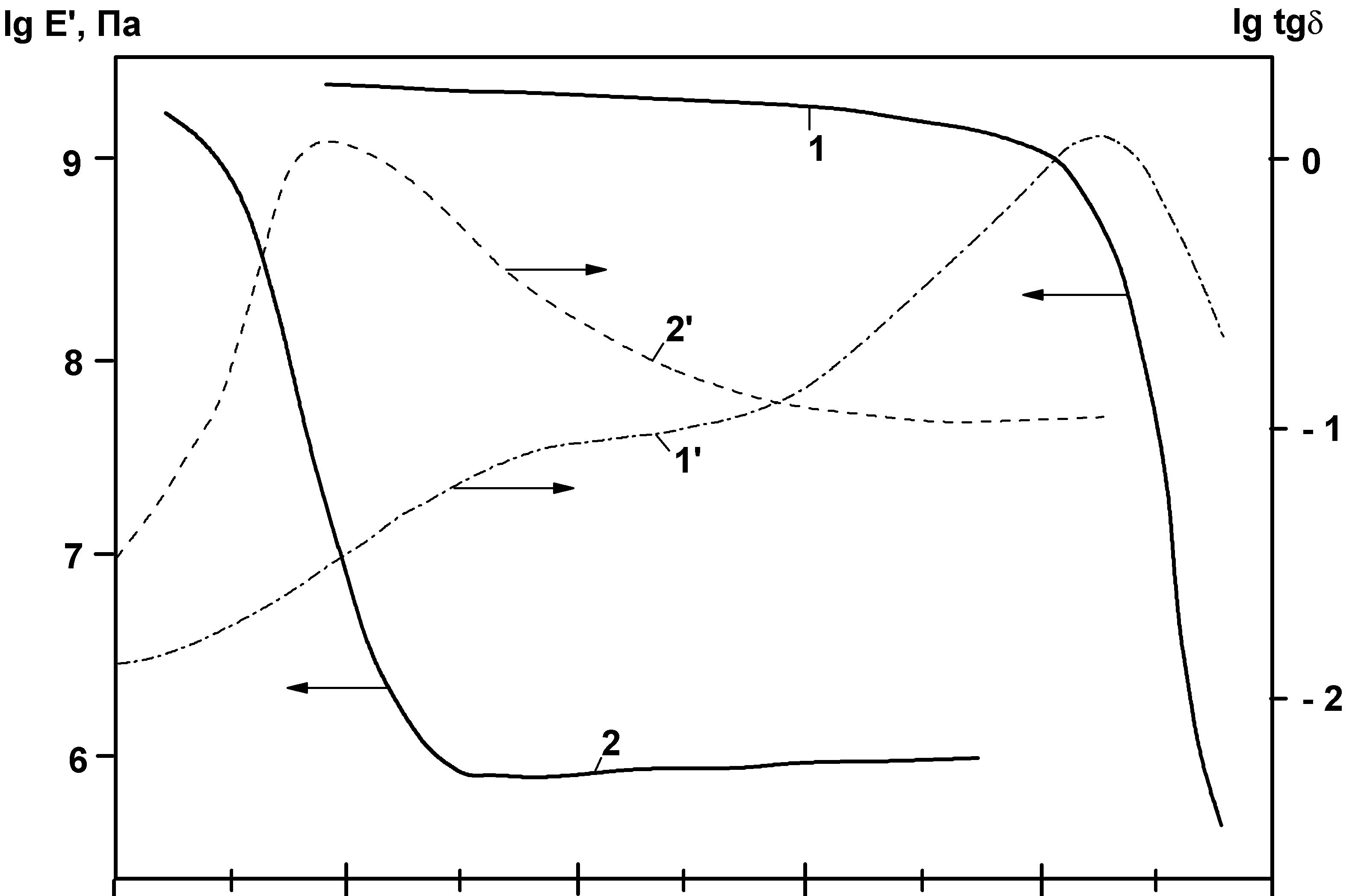
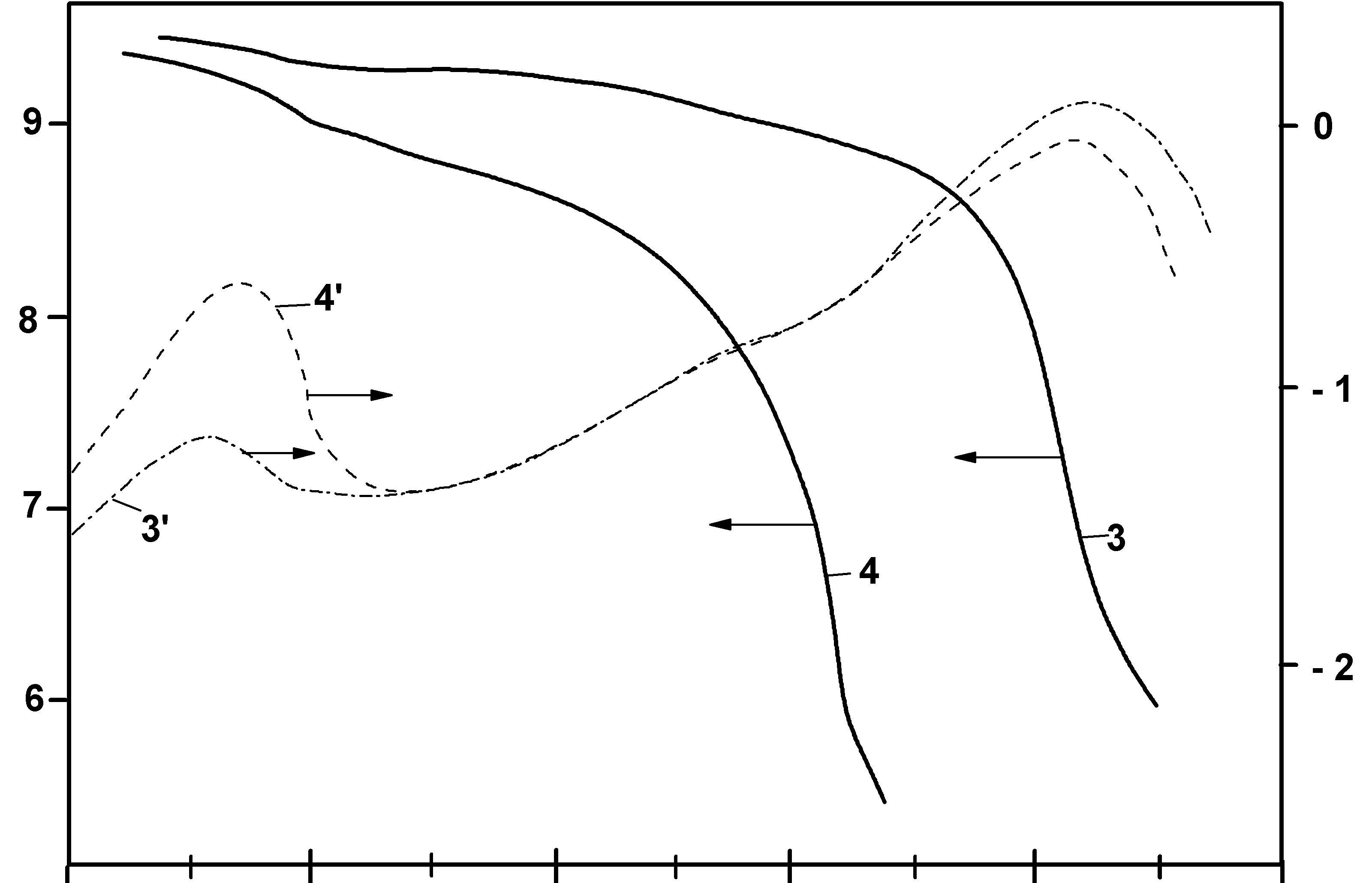
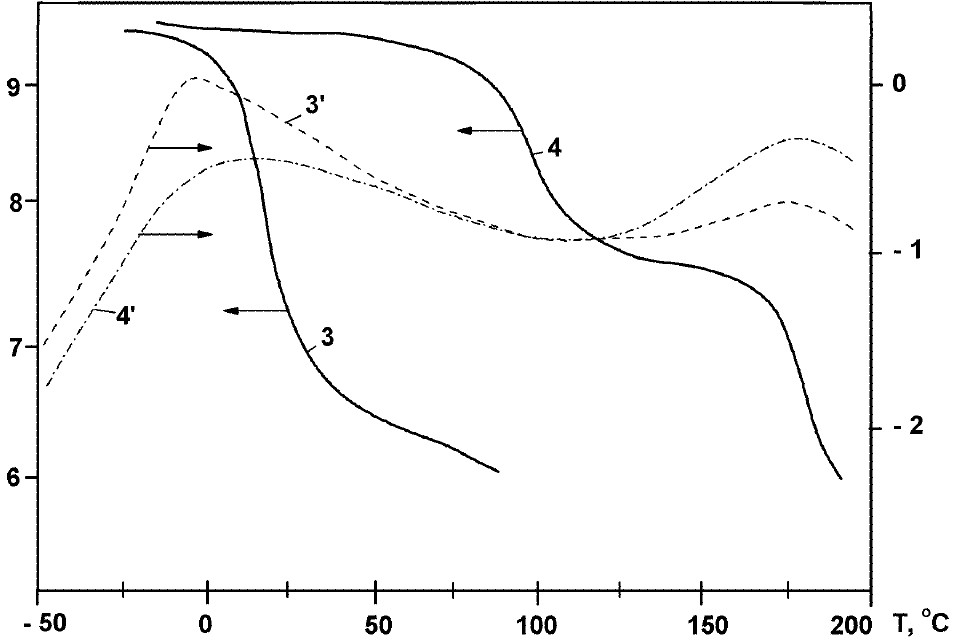
Рис.4.19. Динамические термомеханические спектры (при частоте 110 Гц) в координатах Е΄ (1-4) и tgδ (1΄-4΄): (а) экспериментально полученные для стеклообразного при комнатной температуре полимера (ПММА, кривые 1,1΄) и эластичного при комнатной температуре полимера (ПБА, кривые 2,2΄); (б,в) рассчитанные для их смесей в предположении, что они образуют матричные дисперсии со стеклообразной (б) и эластичной (в) при нормальных условиях матрицей и содержании дисперсной фазы (эластичной и стеклообразной соответственно) 0,25 (кривые 3,3΄ ) и 0,75 (кривые 4,4΄ ) объемных долей
Привденные результаты показывают, что определяющий вклад в механический релаксационный спектр вносит матрица и ее объемная доля. Очевидно, что в реальных гетерогенных системах каждая фаза не будет чистым компонентом и должна содержать, помимо основного компонента, определенное количество другого компонента, что определяется диаграммой состояния смеси. В этом случае расчеты вязко-упругих свойств и механического спектра значительно усложняются: сначала необходимо рассчитать вязко-упругие свойства и их температурные или частотные зависимости для каждой фазы, представляющией собой гомогенную смесь исходных компонентов при заданном их соотношении, определяемом по фазовой диаграмме, и только потом проводить соответствующие расчеты для гетерофазной системы в целом при заданной ее топологии и объемном соотношении фаз, также определяемом по фазовой диаграмме. Для расчетов вязко-упругих свойств гомогенных смесей и их температурных или частотных зависимостей, как и для гомогенных при заданном соотношении компонентов, хорошие результаты дают правила аддитивности. Еще более сложные ситуации наблюдаются при формировании гетерофазных систем с участием блок- или привитых сополимеров ограниченно совместимых некристаллизующихся компонентов, в которых практически всегда происходит микрофазное аморфное разделение с формированием сложной фазовой морфологии и межфазных слоев различного состава.
На рис.4.20а приведены динамические термомеханические кривые при частоте 1 Гц для гетерогенной смеси (в предположении в форме матричной дисперсии) двух некристаллизующихся ограниченно совместимых полимеров (поливинилацетата, ПВА и полибутилакрилата, ПБА) в соотношении 1:1: экспериментально определенный (точки) и рассчитанные при допущениях, что матрица смеси состоит из ПВА (сплошные линии) и из ПБА (штриховые линии), а на рис. 4.20б – такие же кривые для гомогенного статистического сополимера ПВА-ПБА (расчетные данные по правилу аддитивности – сплошные линии, эксприментально полученные данные – штриховые):
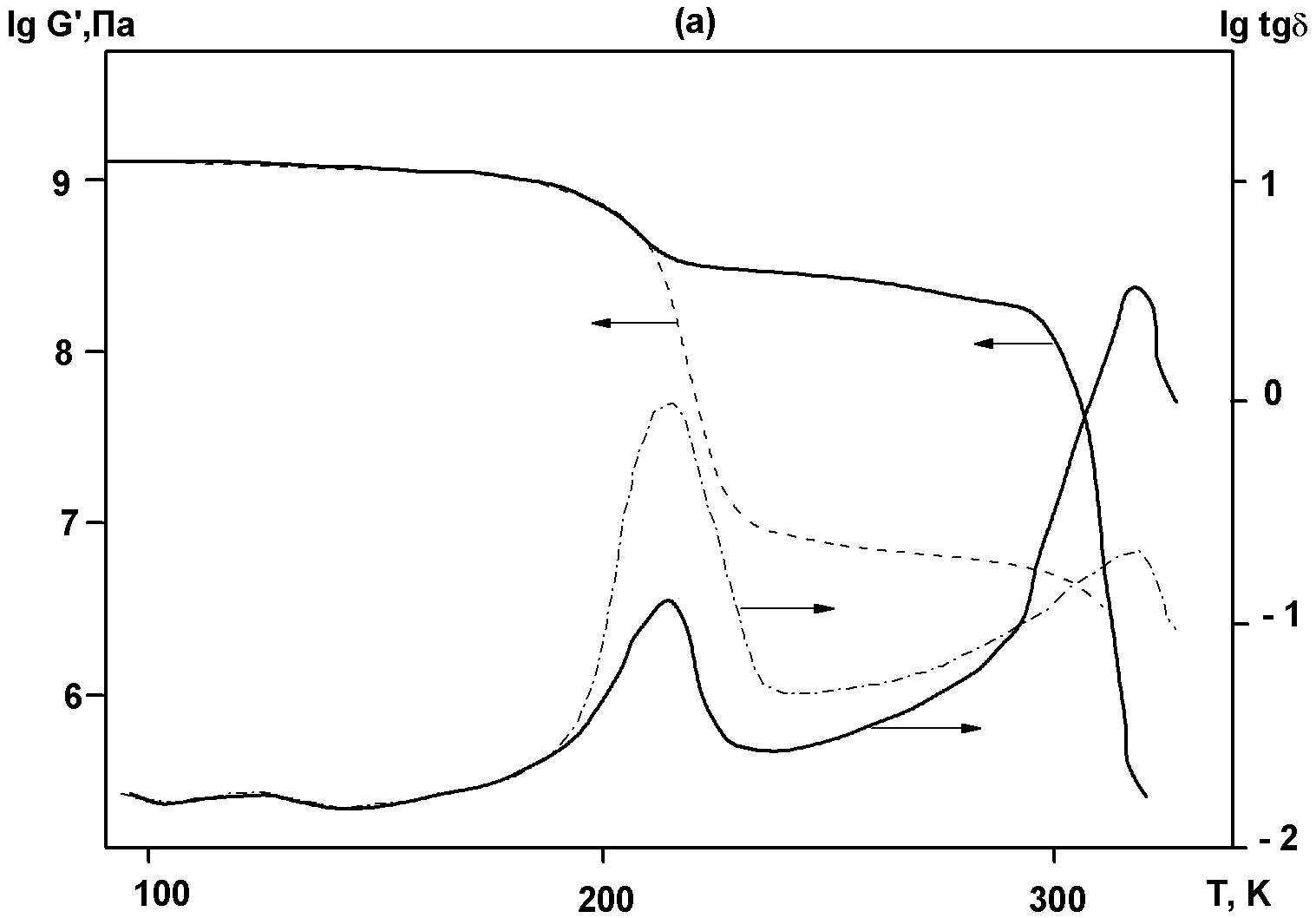
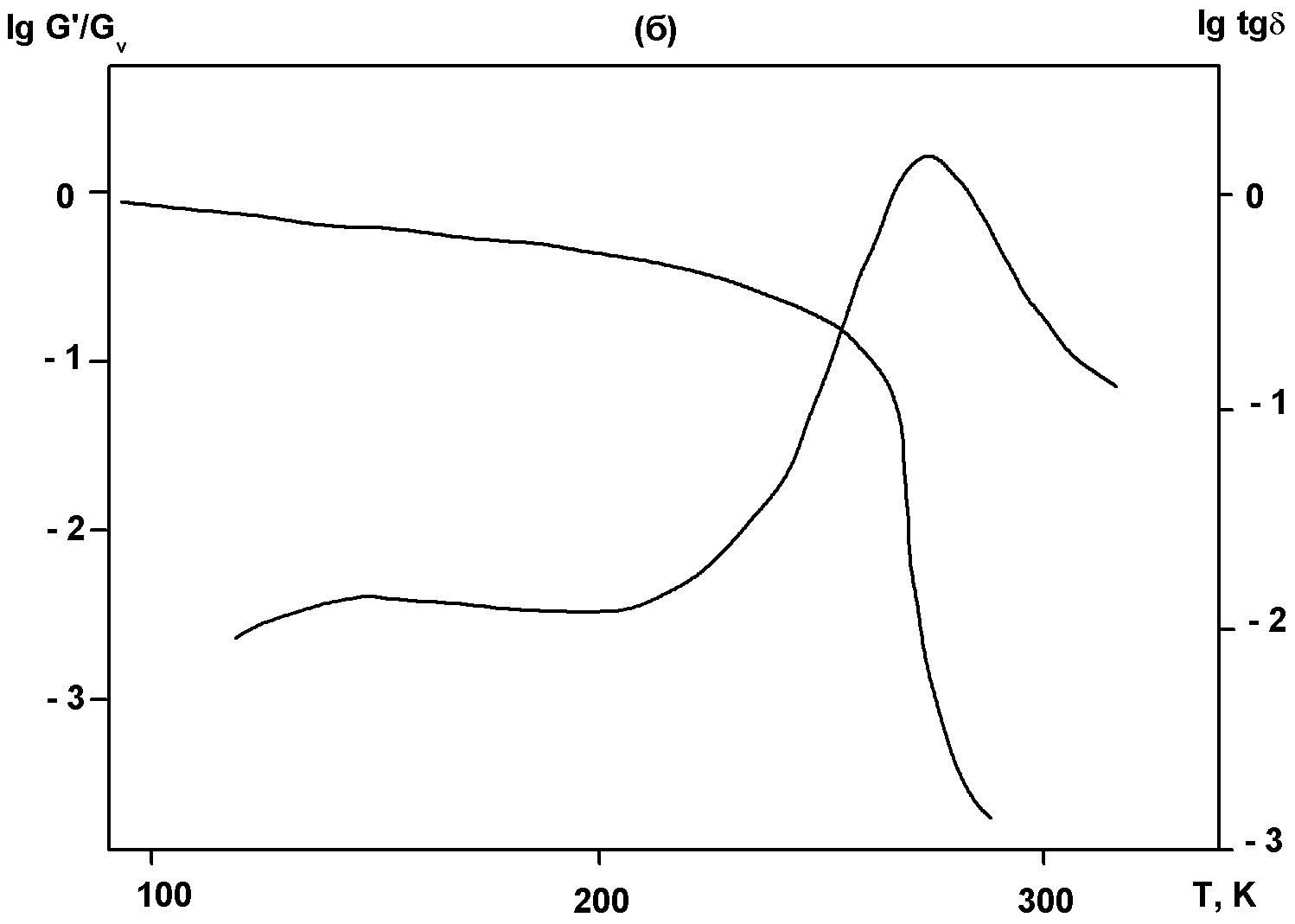
Рис.4.20. а) Динамические термомеханические спектры (при частоте 1 Гц) для гетерогенной смеси в форме матричной дисперсии двух некристаллизующихся ограниченно совместимых полимеров (поливинилацетата, ПВА и полибутилакрилата, ПБА) в соотношении 1:1: экспериментально определенный (точки) и рассчитанные при допущениях, что матрица смеси состоит из ПВА (сплошные линии) и из ПБА (штриховые линии); б) аналогичные спектры для гомогенного статистического сополимера ПВА-ПБА такого же состава - расчетные данные по правилу аддитивности (сплошные линии), экспериментально полученные данные – штриховые линии).
Приведенные результаты показывают, что для гетерогенной смеси только первое допущение дает расчетные кривые, близкие к экспериментально полученным. В случае гомогенных смесей и статистических сополимеров расчетные методы дают хорошее согласие с результатами экспериментов. Положение пика α-релаксации для гомогенной смеси (Тα) при этом удовлетворительно описывается обратным правилом аддитивности (правилом Фокса) [Perez,с.129]:
 ,
(4.1)
,
(4.1)
где φ1, φ2, Тα1, Тα2 – объемные доли и температуры α-пика некристаллизующихся совместимых компонентов 1 и 2 соответственно.
На рис. 4.21а,б приведены динамические термомеханические кривые при частоте 1 Гц для гетерофазных систем ПВА-ПБА, полученных различными методами блок-сополимеризации исходных мономеров при соотношении компонентов 1:1. При этом предполагалось, что в первом случае (а) сформировалась дисперсия, матрица которой состоит преимущественно из ПВА, а частицы ПБА содержат некоторое количество ПВА, а во втором случае (б) в системе сформировался межфазный слой, состав которого меняется от практически чистого ПВА до чистого ПБА в направлении от матрицы ПВА к центру частиц ПБА. На обоих рисунках показаны экспериментально определенные (точки) и рассчитанные данные (сплошные линии). На Рис. 4.21б штриховыми линиями показаны кривые, рассчитанные без учета межфазного слоя.
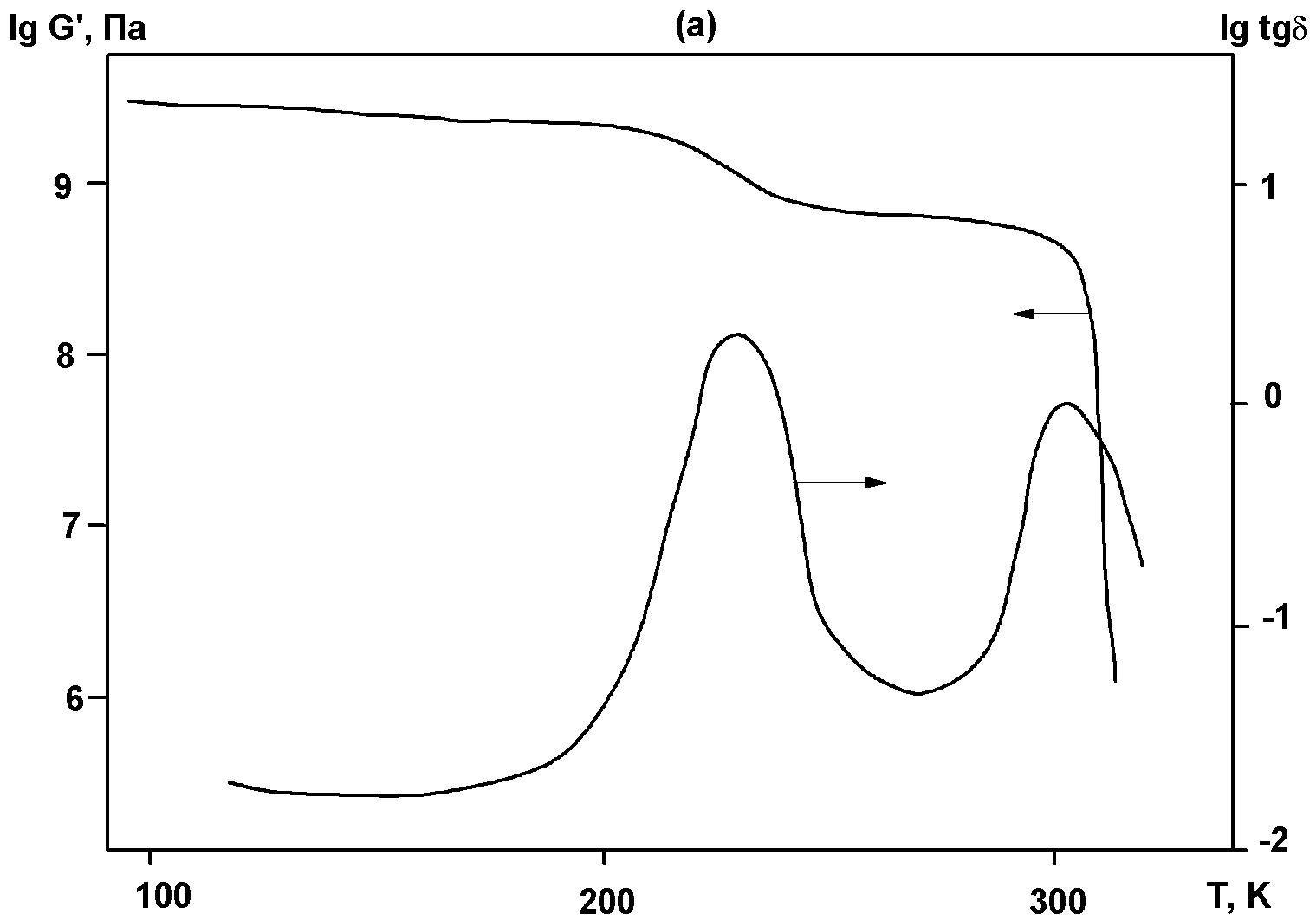
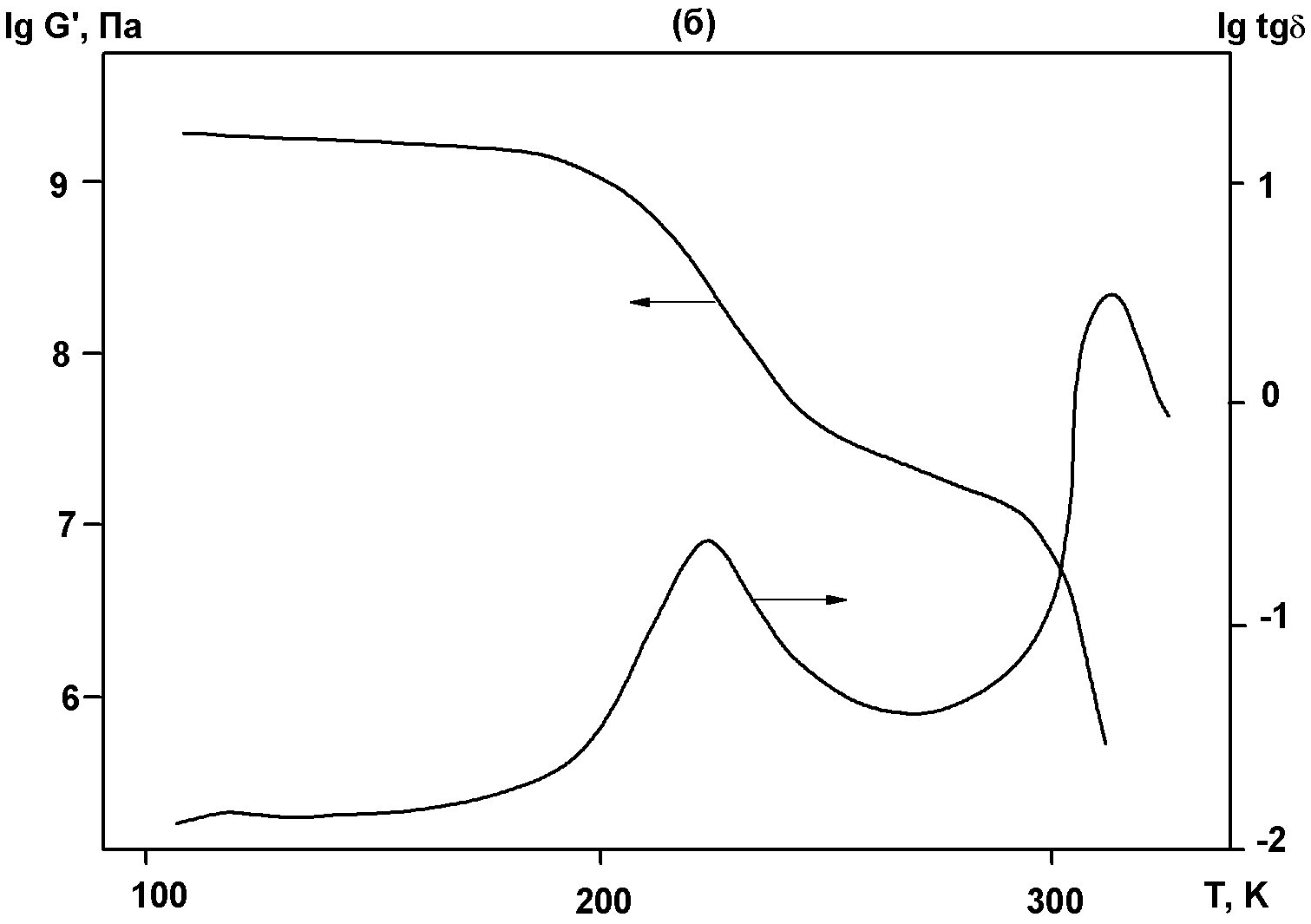
Рис.4.21. Расчетные (сплошные линии) и экспериментально полученные (точки) динамические термомеханические спектры (при частоте 1 Гц) для гетерофазных систем ПВА-ПБА, полученных различными методами блок-сополимеризации исходных мономеров при соотношении компонентов 1:1, в предположениях о формировании дисперсии, матрица которой состоит преимущественно из ПВА, а частицы ПБА содержат некоторое количество ПВА (а), и дисперсии с межфазным слоем, состав которого меняется от практически чистого ПВА до чистого ПБА в направлении от матрицы ПВА к центру частиц ПБА (б). Штриховыми линиями показан спектр, рассчитанный без учета межфазного слоя.
Таким образом, при использовании соответствующих моделей и теоретических подходов динамические термомеханические спектры позволяют в некоторых случаях определять состав фаз и межфазных слоев, а также фазовую морфологию аморфных гетерофазных ПМ. Механические спектры гетерогенных смесей двух ограниченно совместимых полимеров, состоящих из двух фаз, являются практически аддитивной суммой спектров этих компонентов. При известных вязко-упругих параметрах компонентов и их температурных или частотных зависимостях и при известной или заданной фазовой морфологии композиций такие спектры могут быть легко рассчитаны.
Эффекты отжига (физического старения) и закалки проявляются в механических спектрах двухфазных аморфных полимерных композиций, как и аморфно-кристаллических полимеров, через соответствующее изменение состава фаз и фазовой морфологии и обычно ответственны за несовпадение спектров, полученных при нагревании и охлаждении или при различной скорости изменения температуры. Ориентационные эффекты проявляются в изменении формы фазовых образований и появлении анизотропии структуры и свойств полимера.
В случае наполненных или армированных твердыми частицам полимеров днамические термомеханические спектры позволяют оценивать влияние твердой поверхности на структуру и молекулярную подвижность в межфазном слое полимерной матрицы. На рис.4.22 в качестве примера показано изменение характера температурных кривых показателя механических потерь в областях α-, β- и γ-релаксации полигидроксиэфира ПГЭ)на основе бисфенола А и эпихлоргидрина при наполнении его порошком слюды, необработанным и обработанным антиадгезивом – диметилдихлорсиланом (ДМДХС).
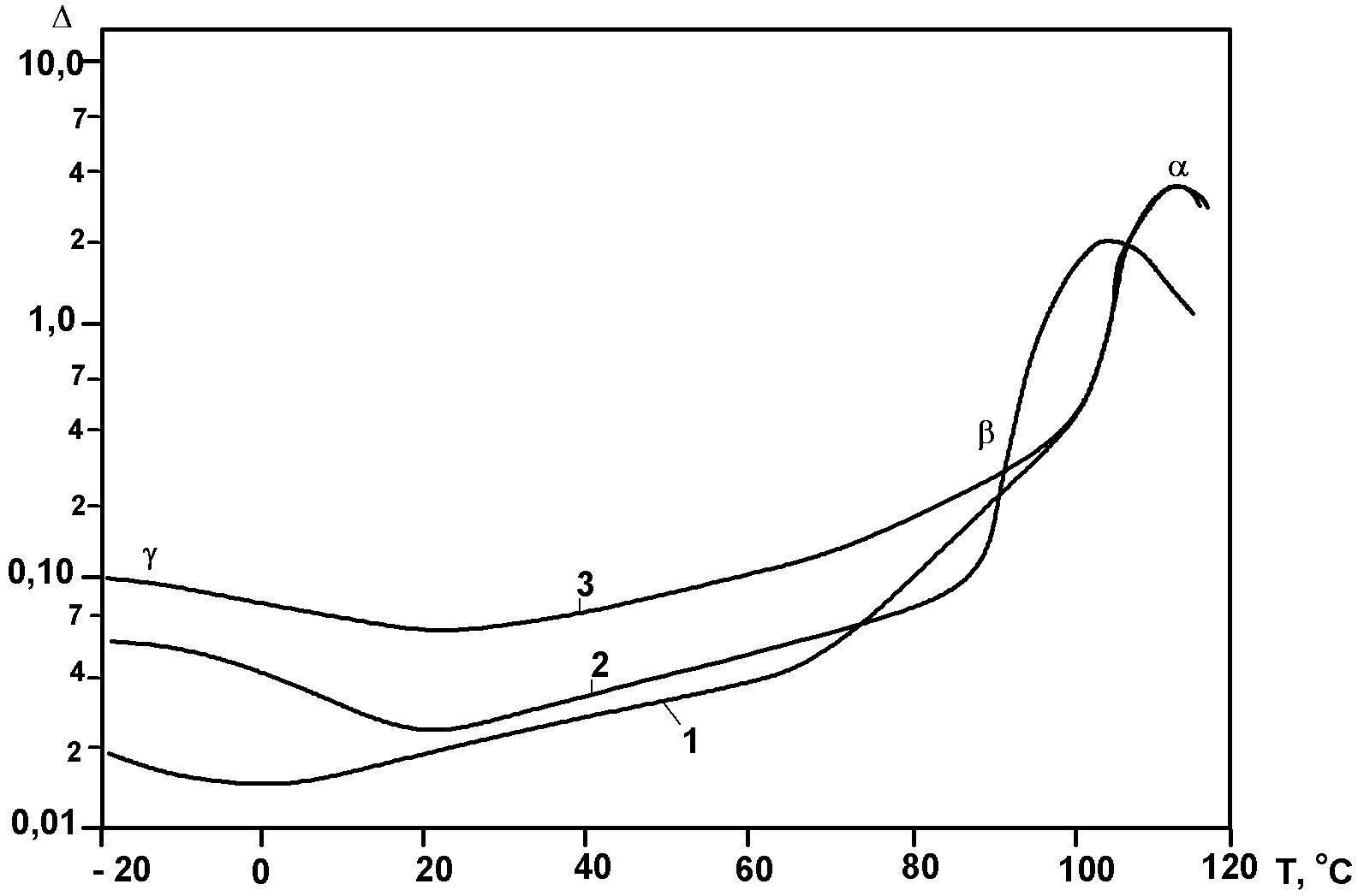
Рис.4.22. Динамические термомеханические спектры (при частоте 1 Гц) в координатах логарифмического декремента затухания для ПГЭ, ненаполненного (1) и дисперсно-наполненного необработанным (2) и обработанным ДМДХС порошком слюды
[Нильсен.с.248,рис.7.19]
Видно, что дисперсный наполнитель, особенно обработанный антиадгезивом, резко повышает общий уровень механических потерь и, соответственно, высоту пиков потерь в области α- и γ-релаксации, что вероятнее всего обусловлено особенностями взаимодействия полимерной матрицы с поверхностью минерального наполнителя и распределения его частиц в композиции
Таким образом, анализ теоретических основ и примеров практического применения методов механической спектрометрии показывает, что она является очень эффективным и информативным методом исследования полимеров, полимерных композиций и материалов на их основе, в том числе композиционных полимерных материалов различного типа и состава с различной молекулярной, надмолекулярной и фазовой структурой компонентов в различных условиях внешней среды и различных внешних воздействий. Измерения статических и динамических параметров вязко-упругих и упруго-вязких свойств таких систем, в особенности их зависимостей от температурных и временных или частотных условий нагружения или деформирования (механических спектров), имеют большое чисто практическое значение при решении многих инженерных материаловедческих и технологических задач и играют важнейшую роль в теоретическом полимерном материаловедении и разработке научных основ их технологий. Если в первом случае достаточно использовать феноменологические соотношения для интерпретации экспериментально полученных данных, то во втором необходима интерпретация тех же результатов на различных структурных, в первую очередь молекулярном, надмолекулярном и фазовом, уровнях.
