48

Бабаевский П.Г.

II. Механические свойства полимеров

II.1.Деформационные свойства полимеров при малых нагрузках и деформациях

II.1.1. Мгновенные упругие (гуковские и высокоэластические) деформации и установившееся вязкое течение аморфных полимеров.

А) Мгновенные упругие (гуковские и высокоэластические) деформации

Существование двух принципиально различных по природе упругих (равновесных обратимых) деформаций полимеров вытекает из равенства максимальной работы деформирования конденсированного тела dA = FdL +pdV и изменения при этом его свободной энергии dG=dU+ pdV –TdS: FdL =dU–TdS, или в виде частных производных:

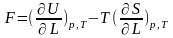, (1.1)

где А-работа, F – сила, L - длина, р-давление, V-объем, G-свободная энергия, U-внутренняя энергия, T-абсолютная температура, S – энтропия.

Из соотношения (1.1) видно, что усилие деформирования и, соответственно, сами деформации подразделяется на две составляющие, а и упругость – на два типа: энергетическую и энтропийную, связанные с увеличением внутренней энергии при деформировании внутри- и межмолекулярных связей и с уменьшением энтропии при изменении конформаций цепей в результате сегментального теплового движения. Энергетическая упругость полимеров, в зависимости от их фазового состояния и структуры определяется деформированием или ковалентнтных и ван-дер-ваальсовских связей, или и тех и других. Усилие будет направлено на деформирование ковалентных связей только в случае ориентированной кристаллической структуры с выпрямленными цепями или жидкокристаллической нематической структуры при приложении силы в направлении ориентации. Во всех остальных случаях деформированию будут подвергаться только более слабые ван-дер-ваальсовские связи. Так как усилие деформирования любой связи определяется ее энергией, точнее наклоном кривой зависимости производной энергии по расстоянию, т.е силы, от межатомного или межмолекулярного расстояния, а также частотой и амплитудой высокочастотных тепловых колебаний, то очевидно, что деформирование любых связей должно быть практически мгновенным, а усилие, необходимое на деформирование ковалентных связей, должно значительно (примерно на три десятичных порядка больше, чем ван-дер-ваальсовских. Изменения конформаций полимерных цепей, т.е. высокоэластические деформации, не сопровождаются изменением внутренней энергии, а только уменьшением энтропии цепей, зависящим от их длины. На это затрачивается значительно меньше энергии и, соответственно, требуется значительно меньшая сила, но этот процесс протекает значительно медленнее. Следовательно, для достижения равновесных высокоэластических деформаций требуется значительно меньшее (примерно на 2-3 десятичных порядка по сравнению с деформированием ван-дер-ваальсовских связей) усилие, но значительно большее время.

Мерой усилия (напряжения), необходимого для развития единичной относительной деформации служат модули упругости (коэффициенты пропорциональности в законе Гука), которые в зависимости от вида нагружения или деформирования соответствуют модулю Юнга (при растяжении/сжатии) Е, модулю при сдвиге G и объемному модулю К, Соответствующие им напряжения и деформации обозначаются обычно: σ и ε, τ и γ, Δр и ΔV. Величины, обратные модулю Юнга и модулю при сдвиге, называются податливостями D и J соответственно, а величина, обратная объемному модулю – изотермической сжимаемостью β. В общей теории упругости связи между модулями упругости и податливостями устанавливаются через коэффициент Пуассона ν, характеризующий изменение объема тела при растяжении или сжатии: E=2G(1+ ν)=3K(1-2 ν); .

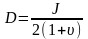Модули энергетической упругости полимеров при деформировании только ковалентных связей могут достигать значений порядка сотен ГПа, тогда как при деформировании только ван-дер-ваальсовских связей – нескольких (2-4) ГПа. Коэффициент Пуассона при этом лежит в интервале 0,2-0,3. Модули энтропийной упругости, или равновесные модули высокоэластичности при растяжении/сжатии и при сдвиге, в зависимости от густоты сетки полимерных цепей, составляют величины от нескольких единиц МПа до нескольких десятков МПа. Значения модуля объемного сжатия при этом лежит в области нескольких ГПа или даже больше, а коэффициент Пуассона близок к 0,5.

Мгновенные модули энергетической упругости и равновесные модули энтропийной упругости или высокоэластичности являются предельными характеристиками вязко-упругих и упруго-вязких свойств (см. следующий раздел 2) полимеров (G_o и G_∞), соответствующих условиям t/θ_α‹‹1 или ωθ_α››1 и t/θ_α››1 или ωθ_α‹‹1 соответственно, где t и ω – временные и частотные условия нагружения или деформирования, θ_α – время релаксации сегментального движения. Они могут быть экспериментально определены при этих условиях или рассчитаны теоретически, исходя из классических молекулярно-кинетических представлений о равновесных упругих деформациях в идеальных стеклообразном и высокоэластическом состояниях соответственно.

В идеальном стеклообразном состоянии однофазных аморфных ПМ, в которых цепи находятся в состоянии заторможенного сегментального движения, при отсутствии дальнего координационного и ориентационного порядка в упаковке ковалентно связанных атомов, групп и звеньев со слабыми межмолекулярными, преимущественно ван-дер-ваальсовскими связями, возможны только высокочастотные колебания, поэтому основными деформациями являются мгновенно упругие, обусловленные деформированием наиболее слабых ван-дер-ваальсовских связей. В соответствии с молекулярно-кинетическими представлениями о таких деформациях модули энергетической мгновенной упругости (E_U=Е_о, G_U=G_о и K_U=К_о) лежат в интервале нескольких (от 3 до 4) ГПа при коэффициенте Пуассона порядка 0.33 и возрастают с понижением температуры пропорционально удвоенному коэффициенту объемного теплового расширения.

В идеальном высокоэластическом состоянии аморфных ПМ сетчатой структуры, в котором цепи между узлами сетки при механическом нагружении способны изменять свои конформации в результате крупномасштабного кооперативного сегментального движения (-формы), но не могут проявлять диффузионную подвижность в целом, превалирующими являются замедленные упругие (высокоэластические) деформации. В соответствие с молекулярно-кинетическими представлениями о таких деформациях и статистической теорией эластичности редких полимерных сеток при небольших равновесных деформациях сдвига соблюдается прямая пропорциональность между сдвиговым напряжением  и относительной деформацией  (закон Гука), причем значение коэффициента пропорциональности (равновесного модуля высокоэластичности при сдвиге G_R=G_∞) теоретически может быть рассчитано по следующей формуле [ ]:

, (1.2а)

где: Ф - коэффициент, учитывающий неидеальность структуры полимерной cетки и гибкости цепей (близок к 1); - показатель густоты сетки, равный числу молей цепей между узлами сетки в единице объема (М_с – средняя молекулярная масса цепей между узлами сетки;  - плотность полимера) и связанный с показателем частоты узлов сетки _с (числом молей узлов в единице объема) соотношением: 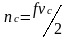, где f – функциональность узлов сетки (число цепей, сходящихся в одном узле); R – универсальная постоянная, Т – абсолютная температура.

При образовании полимерной сетки в результате поперечного соединения (сшивания) линейных макромолекул неидеальность (дефектность) структуры сетки, обусловленная несшитыми концами макромолекул, учитывается следующим образом [Трелоар, с.70]:

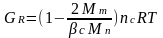, (1.2б)

где: M_m, M_n - молекулярная масса повторяющегося мономерного звена и макромолекулы в целом соответственно; _с – степень сшивания, или доля сшитых мономерных звеньев.

Для небольших равновесных деформаций растяжения/сжатия эластичных полимерных сеток получены следующие теоретические соотношения между напряжением  и деформацией  (степенью удлинения или сжатия, связанной с относительным удлинением или сжатием  простым соотношением: =1+):

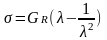
, (1.3)

где: , _ - напряжение при растяжении/сжатии, рассчитанное по площади поперечного сечения исходного недеформированного и деформированного образца соответственно.

При этом равновесный модуль высокоэластичности при растяжении/сжатии E_R=Е_∞ связан с G_R следующим соотношением:

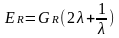(1.4)

При 1: E_R=3G_R=3n_cRT (1.5)

Равенство E_R=3G_R с учетом соотношения из теории упругости (E=2G(1+ν)), свидетельствует, что коэффициент Пуассона ν эластичных полимерных сеток при равновесной деформации теоретически равен 0,5, т.е. что при их растяжении/сжатии не происходит изменения объема. При этом величина равновесного объемного модуля высокоэластичности K_R теоретически стремится к бесконечности, хотя очевидно, что его предельное значение должно быть равно объемному модулю мгновенной упругости K_U, т.к. объемное сжатие эластичных полимерных сеток возможно только за счет деформирования внутри- и межмолекулярных связей. По абсолютной величине объемный модуль мгновенной упругости K_U, как и модули E_U и G_U, на 2-3 десятичных порядка превосходят соответствующие равновесные модули E_R и G_R, величина которых, прямо пропорциональна густоте сетки и температуре и лежит в интервале от единиц до нескольких десятков МПа.

При набухании эластичного редкосетчатого полимера в растворителе равновесные модули E_R и G_R уменьшаются пропорционально степени набухания, или объемной доле полимера в набухшем состоянии _r в степени 1/3 [Трелоар, с.75].

Замедленный (релаксационный) характер процессов высокоэластических деформаций редкосетчатых полимеров обусловлен, в первую очередь, трением сегментов о вязкую среду. Это трение может быть выражено в терминах внутренней вязкости при сдвиге _R, величина которой связана с равновесным модулем высокоэластичности при сдвиге G_R через время релаксации -формы сегментального движения:

_R= G_R_ (1.6)

Температурная зависимость _R в решающей степени определяется экспоненциальной зависимостью от температуры времени релаксации при малой зависимости от температуры G_R (см. соотношение 1.1). Зависимость внутренней вязкости от давления описывается экспоненциальной функцией [Малк.,с.207]:

, (1.7)

где: _R(P), _R(P₀) – внутренняя вязкость при давлении Р и при нормальном давлении P₀ соответственно;  - константа.

Таким образом очевидно, что в высокоэластическом состоянии аморфные полимеры проявляют резко выраженные эффекты механической релаксации и вязко-упругости, связанные с зависимостью их вязко-упругих свойств от температурно-временных условий нагружения и деформирования, особенно при условии, что t/θ_α или _ близки к 1. Равновесный модуль высокоэластичности соответствует нерелаксируемому модулю при t_. Нерелаксируемый модуль при t_ (при кинетическом стекловании) соответствует мгновенному модулю упругости.

Б) Установившееся вязкое течение расплавов и растворов полимеров.

В вязко-текучем аморфном состоянии (в расплавах или растворах) полимеров превалирующей деформацией является вязкое течение, связанное с макроброуновским движением цепей, которое резко отличается для изолированных клубков цепей в разбавленных растворах и для перепутанных цепей в концентрированных растворах и расплавах полимеров. Важнейшей характеристикой вязкого течения расплавов и растворов полимеров является их вязкость при установившемся течении, т.е. при скорости деформирования, стремящейся к нулю: начальная или нулевая (ньютоновская) вязкость ₀. При реальных скоростях деформирования растворы и расплавы полимеров ведут себя как типичные упруго-вязкие (аномальные, или неньютоновские) жидкости вследствие появления ориентационных эффектов гибких полимерных цепей – вязкость зависит от скорости деформирования, а упругость проявляется в эластодинамических эффектах – возникновении нормальных напряжений при действии сдвиговых [ ].

В этом разделе рассматривается только вязкость полимеров при сдвиге. Продольная вязкость при растяжении или сжатии _l связана с вязкостью при сдвиге  соотношением η_l=2η(1+ ν), и при отсутствии резко выраженных ориентационных эффектов (при установившемся течении) _l =3.

Начальная, или ньютоновская вязкость η₀ при бесконечно малых скоростях деформирования, также как мгновенные модули энергетической упругости и равновесные модули энтропийной упругости или высокоэластичности, является предельной характеристикой вязко-упругих и упруго-вязких свойств (см. следующий раздел 2) при t/θ_m››1 или ωθ_m‹‹1 соответственно, где t и ω – временные и частотные условия нагружения или деформирования, θ_m – время релаксации макроброуновского движения (макроскопическое время релаксации).

Ньютоновская вязкость расплавов полимеров в решающей степени определяется их молекулярной массой (длиной цепей) и температурой В общем случае зависимость ньютоновской вязкости от молекулярной массы описывается степенным уравнением:

, (1.8)

где К –константа, зависящая от гибкости цепей, М – молекулярная масса, a – константа, зависящая от возможности образования зацеплений цепей: ее значение изменяется от величины порядка единицы до 3,4 при прохождении молекулярной массой некоторого критического значения, лежащего для различных полимеров в интервале 10⁴-4∙10⁴ и соответствующего возможности образования сетки зацеплений цепей.

Течение разбавленных растворов полимеров при нулевой скорости сдвига определяется поступательным и вращательным движением набухших макромолекулярных клубков в среде растворителя с вязкостью _s, и начальная вязкость таких растворов описывается уравнением Эйнштейна для дисперсий сферических частиц в вязкой среде:

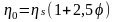, (1.9)

где:  - объемная доля макромолекулярных клубков в растворе, пропорциональная их концентрации с и числу сегментов N или молекулярной массе M в степени , зависящей от набухания клубков в растворе, т.е. от «качества» растворителя (в -условиях =0,5, в хорошем растворителе - 4/5).

Относительный вклад полимерных клубков в начальную вязкость разбавленных растворов оценивается инкрементом вязкости (разностью вязкости раствора и растворителя) и характеристической вязкостью [] (пределом отношения инкремента вязкости к вязкости растворителя при его концентрации, стремящейся к нулю). Оба эти параметра, также как и ₀,пропорциональны числу сегментов N в полимерных клубках или их молекулярной массе M в степени .

Вязкое течение концентрированных растворов и расплавов полимеров при нулевой скорости сдвига определяется процессами проползания (рептации) цепей между препятствиями (в «трубке»), создаваемыми соседними цепями. Скорость рептации цепей в решающей степени зависит от длины цепей (их молекулярной массы) и способности образовывать физические узлы, или зацепления. Поэтому при заданных температуре и давлении начальная вязкость концентрированных растворов и расплавов полимеров пропорциональна числу сегментов N и молекулярной массе M в степени α , где α – константа, зависящая от гибкости цепей и образования ими лабильных зацеплений: при отсутствии зацеплений (ММе) значение α близо к 1, а при наличии зацеплений (М Ме) – равно примерно 3,3-3.4, где Ме – молекулярная масса цепей между зацеплениями, или критическая молекулярная масса (для гибкоцепных полимеров Ме лежит в интервале 10³-10⁴ ). Получено теоретическое соотношение, связывающее начальную вязкость расплавов гибкоцепных линейных полимеров с их молекулярным строением и подвижностью [Аск.,с.202[177]:

, (1.10)

где: 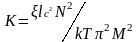- коэффициент, учитывающий внутреннее трение сегментов:  - коэффициент внутреннего, l_c, N – длина и число сегментов цепей соответственно, M, M_e – средняя молекулярная масса цепей и участков цепей между зацеплениями соответственно, k – константа Больцмана; R - универсальная постоянная; T – абсолютная температура;  - плотность полимера.

Начальная вязкость концентрированных растворов полимеров η₀ экспоненциально зависит от концентрации низковязкого растворителя с_s[Малк.,с.218]:

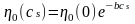, (1.11)

₀(0) – начальная вязкость расплава полимера; b – константа, зависящая от природы полимера и растворителя.

Температурные зависимости начальной вязкости расплавов и растворов полимеров при термодинамических параметрах, соответствующих их равновесному жидкому состоянию, т.е. при температуре выше температуры фазового перехода 1-го рода, описываются уравнением Аррениуса. В метастабильном переохлажденном состоянии при Т›Т_m(температуры потери текучести вследствие образования непрерывной сетки зацеплений цепей) эти зависимости хорошо описываются уравнением ВЛФ, а при приближении к T_m – уравнением ФФТ.