
- •3.3 Силовой расчет группы звеньев 2-3………………………………..……….13
- •1. Структурный анализ механизма
- •2. Кинематический анализ рычажного механизма.
- •2.1 Построение 12 положений рычажного механизма.
- •2.2 Построение планов скоростей.
- •2.3 Построение планов ускорений.
- •3. Силовой анализ плоского рычажного механизма.
- •3.1 Определение нагрузок, действующих на звенья механизма.
- •4.Рычаг Жуковского
- •5. Синтез кулачкового механизма.
- •5.3 Построение профиля кулачка.
- •6. Синтез зубчатого механизма
3. Силовой анализ плоского рычажного механизма.
Дано:
а=410 мм;
b=70 мм;
c=70 мм;
lОА=120 мм;
lАВ=550 мм;
lВО1=400 мм;
lBD=240 мм;
lDE=1400 мм;
ω = 14 с-1;
Fmax= 7 кН;
δ = 0,06;
mм = 30 кг/м;
mE = 50 кг;
g=9.8 м/с2
3.1 Определение нагрузок, действующих на звенья механизма.
Вычислим силы тяжести. Равнодействующие этих сил расположены в центрах масс звеньев, а величины равны:
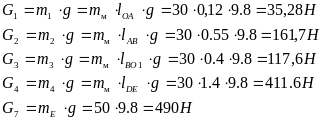
Найдём силу полезного сопротивления по диаграмме сил полезных сопротивлений. Для рассматриваемого положения механизма эта сила равна FH=525 H
Для определения инерционных нагрузок требуются ускорения звеньев и некоторых точек, поэтому воспользуемся планом ускорений для рассматриваемого положения механизма.
Определим силы инерции звеньев. Ведущее звено, как правило, уравновешено, то есть центр масс его лежит на оси вращения, а равнодействующая сил инерции равна нулю. Для определения сил инерции других звеньев механизма предварительно определим ускорения их центров масс:
 Определим
силы инерции:
Определим
силы инерции:

Для определения моментов сил инерции необходимо найти моменты инерции масс звеньев и их угловые ускорения.
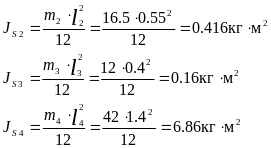
Угловые ускорения звеньев определяются по относительным тангенциальным ускорениям, поэтому:
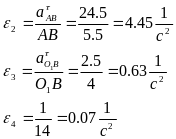
Найдём моменты сил инерции:
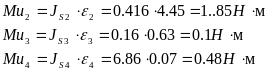
 3.2
Силовой расчёт группы звеньев 4-5.
3.2
Силовой расчёт группы звеньев 4-5.
Выделим из механизма группу звеньев 4-5, расставим все реальные нагрузки и силы и моменты сил инерции.
Действие на рассматриваемую группу отброшенных звеньев заменим силами. В т.Е на ползун 5 действует сила со стороны стойки - направляющей ползуна. В отсутствии трения сила взаимодействия направлена перпендикулярно к контактирующим поверхностям, т. е. перпендикулярно направлению движения ползуна, а влево или вправо, пока не известно, поэтому направим эту силу предварительно вверх. Если после вычислений окажется, что она отрицательна, то необходимо изменить направление на противоположное.
В точке D со стороны звена 3 на звено 4 действует сила F34. Ни величина, ни направление этой силы неизвестны, поэтому определяем её по двум составляющим: одну направим вдоль звена и назовём нормальной составляющей, а вторую перпендикулярно звену и назовём тангенциальной составляющей. Предварительное направление этих составляющих выбираем произвольно, а действительное направление определиться знаком силы после вычислений.
На ползун Е действует ещё сила нагрузки, которая направлена, противоположно ускорению
Расставим на выделенной группе звеньев все перечисленные силы и определим неизвестные реакции в кинематических парах Е, D – R05 и R45.
Сначала определяем тангенциальную составляющую силы R45 из условия равновесия звена 4. Приравняв к нулю сумму моментов сил относительно точки Е, получим:
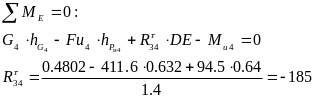
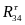 направляем в
противоположную сторону, выбранному
положению.
направляем в
противоположную сторону, выбранному
положению.
Нормальная составляющая силы R34 и сила R05 находятся графическим методом из векторного многоугольника, построенного для группы звеньев 4,5. Известно, что при силовом равновесии многоугольник, составленный из векторов сил, должен быть замкнутым.
3.3 Силовой расчёт группы звеньев 2-3.
Выделим из механизма группу звеньев 2, 3, расставим все реальные нагрузки и силы и моменты сил инерции, реакции отброшенных звеньев. В точке B действует сила R43, которая равна R34 и направлена противоположно ей.
Неизвестными являются: сила взаимодействия 1 и 2 звена.
 В
точке B со стороны звена 2 на звено 3
действует сила R12.
Ни величина, ни направление этой силы
неизвестны, поэтому определяем её по
двум составляющим: одну направим вдоль
звена и назовём нормальной составляющей,
а вторую перпендикулярно звену и назовём
тангенциальной составляющей.
Предварительное направление этих
составляющих выбираем произвольно, а
действительное направление определиться
знаком силы после вычислений.
В
точке B со стороны звена 2 на звено 3
действует сила R12.
Ни величина, ни направление этой силы
неизвестны, поэтому определяем её по
двум составляющим: одну направим вдоль
звена и назовём нормальной составляющей,
а вторую перпендикулярно звену и назовём
тангенциальной составляющей.
Предварительное направление этих
составляющих выбираем произвольно, а
действительное направление определиться
знаком силы после вычислений.
Сначала определяем тангенциальную составляющую силы R12 из условия равновесия звена 3. Приравняв нулю сумму моментов сил относительно точки B, получим:
1)
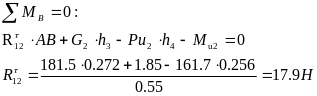
2)
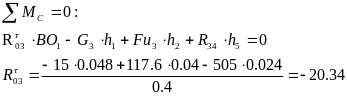
Нормальная составляющая силы R34 и силы R01 находятся графическим методом из векторного многоугольника, построенного для группы звеньев 2.3. Известно, что при силовом равновесии многоугольник, составленный из векторов сил, должен быть замкнутым.
Так как направления линий действия нормальной составляющей силы R34 и R51 известны то, построив предварительно незамкнутый многоугольник из известных векторов сил, можно обеспечить его замыкание, если провести через начало первого и конец последнего вектора прямые, параллельные направлениям искомых сил. Точка пересечения этих прямых определит величины искомых векторов и их действительные направления.
3.4 Силовой расчёт ведущего звена.
На ведущее звено будут действовать силы R12 равная силе R21, но противоположно направленная, уравновешивающая сила Fу и сила R01.
Силы R01 и Fу найдем, построив силовой многоугольник.
Fу=501Н
