МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

ЧЕРКАСЬКИЙ ДЕРЖАВНИЙ ТЕХНОЛОГІЧНИЙ УНІВЕРСИТЕТ

МЕТОДИЧНІ ВКАЗІВКИ

до виконання розрахунково-графічної роботи з дисципліни

“МАТЕМАТИЧНІ ЗАДАЧІ В ЕЛЕКТРОЕНЕРГЕТИЦІ”

для студентів спеціальності

7. 090603 “Електротехнічні системи електроспоживання”

усіх форм навчання

Черкаси ЧДТУ

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

ЧЕРКАСЬКИЙ ДЕРЖАВНИЙ ТЕХНОЛОГІЧНИЙ УНІВЕРСИТЕТ

МЕТОДИЧНІ ВКАЗІВКИ

до виконання розрахунково-графічної роботи з дисципліни

“МАТЕМАТИЧНІ ЗАДАЧІ В ЕЛЕКТРОЕНЕРГЕТИЦІ”

для студентів спеціальності

7. 090603 “Електротехнічні системи електроспоживання”

усіх форм навчання

Затверджено

на засіданні кафедри

електротехнічних систем,

протокол № від . .200_ р.

та Методичною радою ЧДТУ,

протокол № від

Черкаси ЧДТУ

Методичні вказівки до виконання курсової роботи з дисципліни “Математичні задачі в електроенергетиці” для студентів спеціальності 7.090603 “Електротехнічні системи електроспоживання” усіх форм навчання / Укл. К.М. Ключка, М.М. Федосенко, О.С. Гавриш, О.О. Ситник. - Черкаси: ЧДТУ, 200_. - __ с.

Укладачі: Ключка К.М.

Федосенко М.М., к.т.н., доцент

Гавриш О.С., к.ф.-м.н.

Ситник О.О., к.т.н., доцент

1. Загальні вказівки до виконання розрахунково-графічної роботи

Методичні вказівки складені відповідно до програми курсу “Математичні задачі в електроенергетиці” для студентів спеціальності 7.090603 “Електротехнічні системи електроспоживання”. Сформульовано завдання на розрахунково-графічну роботу (РГР) та наведені варіанти індивідуальних вихідних даних для обчислень.

Метою РГР є закріплення та поглиблення знань з лекційного курсу “Математичні задачі в електроенергетиці” і одержання навичок їх використання для розв’язку реальних задач енергетики.

В результаті виконання РГР необхідно розв’язати 4 задачі з наступних тем:

1. випадкові величини в енергетиці та визначення їх числових характеристик; розрахунок параметрів рівняння регресії;

2. системи випадкових величин та їх числові характеристики;

3. критерій згоди Пірсона;

4. моделювання нормального закону розподілу.

Варіанти індивідуальних завдань наведені в розділі 3.

РГР оформлюється на аркушах формату А4, або у зошиті об’ємом 12 аркушів. Необхідно переписати текст задачі і вихідні дані згідно з індивідуальним варіантом, який визначається викладачем. Визначити придатні формули для розрахунків і виконати обчислення за допомогою мікрокалькулятора або ПЕОМ. Побудувати необхідні графіки, які можуть бути розміщені за текстом, або на окремих аркушах у пояснювальній записці. Навести список літератури, яка використовувалася при виконанні РГР. Посилання в тексті пояснювальної записки на першоджерела здійснюється в квадратних дужках з обов’язковим вказування номера сторінки, наприклад [2, стор. 47]. Загальний об'єм ПЗ становить близько 12-16 стор.

Робота повинна бути цілком оформлена і здана на перевірку не пізніше 14-го учбового тижня.

2. Використання апарату теорії імовірностей в практичних задачах енергетики

Наведемо деякі прийоми застосування теорії імовірностей у задачах енергетики, викладаючи їх на конкретних прикладах.

Завдання №1. Виписати 20 значень випадкової величини x і 20 значень випадкової величини y (n=20).

x	14	96	87	36	80	13	86	66	85	73	94	43	26	91	64	14	08	37	93	03
y	00	36	75	02	55	55	29	05	84	63	77	61	54	14	15	00	78	76	74	36

Для випадкової величини знайти:

1. математичне сподівання (m(x), m(y))

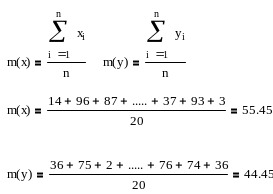
2. дисперсію (Д(x), Д(y))

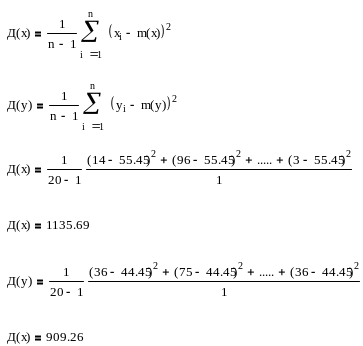
3. середнє квадратичне відхилення ((x), (y))

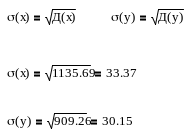
4. асиметрію (As(x), As(y))

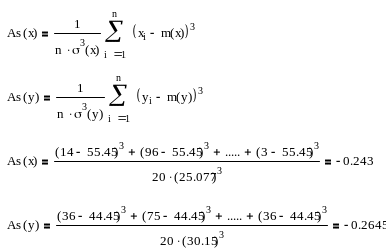
5. ексцес (E(x), E(y))

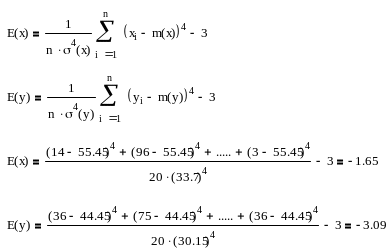
6. Визначити максимум кожної випадкової величини з імовірністю =0,95 (t_=1,643)

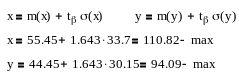
7. Визначити для випадкової величини довірчі інтервали з довірчою імовірністю =0,95 (t'_=1,96) оцінку математичного сподівання

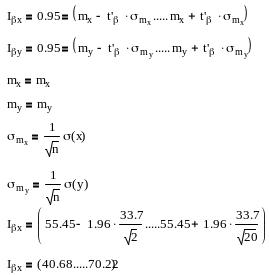
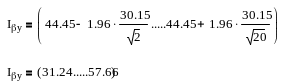
8. Оцінка дисперсії

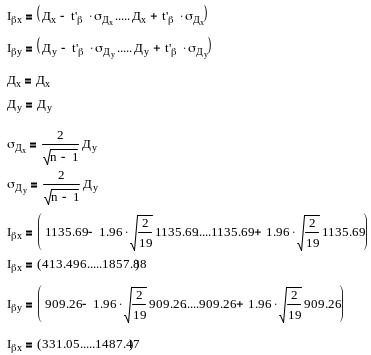
9. Визначити тісноту і наявність кореляційного зв'язку випадкових величин, кореляційний момент K(x,y)

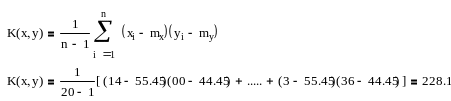
10. Коефіцієнт кореляції r(x,y)

-стійкий слабкий кореляційний зв'язок.

Побудувати розподіл (x_i, y_i), i=1...20

20

2

7

14

15

8

4

16

1

53.36

12

18

13

6

9

5

10

17

11

19

3

y=0.2x+33.36

11. Побудувати параметри рівнянь регресії для 2-х випадків

    • лінійна функція: Y(x)=Ax+B

    • парабола: Y(x)=Ax2+Bx+C

y=ax+b

x	0	100
y	36.36	53.36

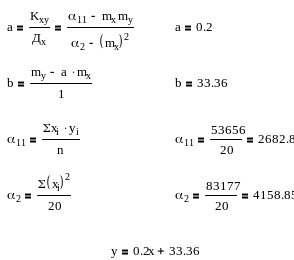
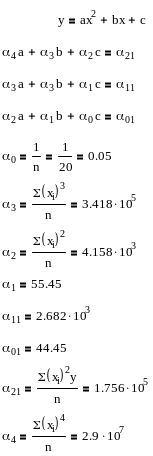
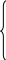
Знаходимо значення коефіцієнтів a, b, c

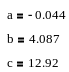
Завдання №2. Навантаження вузлів I_j (j=1,2,3,4,5) схеми, наведеної на рис.2.1, розподілені за нормальним законом.

Визначити розрахункові навантаження вузлів I_рj (j=1...5) та розрахункові сумарні навантаження I_р1-2, I_р3-5, Iр_. Визначити значення коефіцієнтів одночасності (коефіцієнтів попиту) К_о для знайдених розрахункових сумарних навантажень I_р1-2, I_р3-5, Iр_.

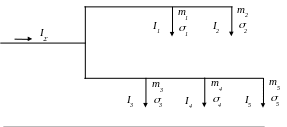
Рисунок 2.1

	1	2	3	4	5
1	1	0.47	0. 215	0.13	0. 455
2		1	0.32	0.07	0.04
3			1	0. 185	0. 465
4				1	0. 015
5					1

Ipj=mij+t__ij t_=1. 643

mij	140	960	870	360	800
ij	39	258	198	255	219
Ipj	204.08	1383. 9	1195. 3	778.96	1159. 8

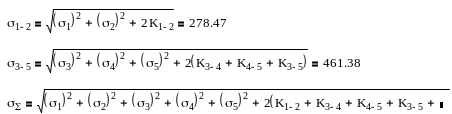
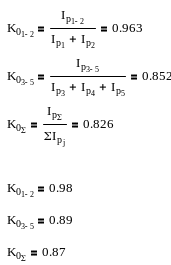
Завдання №3. У залежності від номера варіанта і номера групи з таблиці випадкових чисел виписати n=100 значень із двухзначної випадкової величини по 2 цифри з таблиці на кожне значення випадкового величини.

За допомогою критерію згоди Пірсона (²) перевірити правдоподібність гіпотези про відповідність отриманого розподілу закону рівномірної щільності з параметрами =0, =100.

14		96		87	36	80	13	86	66	85	73	94	43	26	91
64		14		08	37	93	03	00	36	75	02	55	55	29	05
84		63		77	61	54	14	15	00	78	76	74	36	41	67
96		59		57	53	27	64	91	09	06	65	15	21	65	69
36		62		81	30	55	88	46	09	55	84	16	75	50	05
51		12		44	29	83	53	58	01	23	47	22	27	00	18
78		89		13	32	32	79	55	43	13	39	07	21	68	09
86	51

1. Розбиваємо діапазон різних значень на 10 однакових інтервалів m=10, pi=1/m=0.1, nxp_i=100x0. 1=10

	0-10	10-20	20-30	30-40	40-50	50-60	60-70	70-80	80-90	90-100
ni*	14	11	9	9	6	14	11	9	11	6
pi*	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1

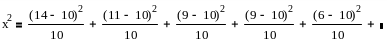
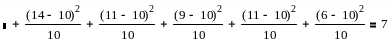
Проводимо інтерполяцію:

Отже гіпотеза правдоподібна.

2. Розбиваємо діапазон можливих значень на 5 однакових інтервалів.

m=5, pi=1/m=0.2, pixn=100x0. 2=20

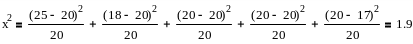
т.е. для х²=1.9, r=3, p>0.1 - гіпотеза правдоподібна

Завдання №4. Використовуємо метод моделювання нормально розподілених чисел шляхом підсумовування k=9 рівномірно розподілених чисел одержати 25 значень випадкового величини Х.

i	Ri,j										i	xi
	1	2	3	4	5	6	7	8	9
1	14	96	87	36	80	13	86	66	85	5.63	1.305	333.96
2	73	94	43	26	91	64	14	08	37	4.5	0	240
3	93	03	00	36	75	02	55	55	29	3.48	-1.778	111.984
4	05	84	63	77	61	54	14	15	00	3.73	0.889	175.992
5	78	76	74	36	41	67	96	59	57	5.84	1.57	353.04
6	53	27	64	91	09	06	65	15	21	3.51	-1.143	157.704
7	65	69	36	62	81	30	55	88	46	5.32	0.947	308.184
8	09	55	84	16	75	50	05	51	12	3.57	-1.074	162.672
9	44	29	83	53	58	01	23	47	22	3.6	-1.039	165.192
10	27	00	18	78	89	13	32	32	79	3.68	-0.947	171.816
11	55	43	13	39	07	21	68	09	86	3.41	-1.259	149.352
12	51	59	07	95	66	15	56	63	34	4.46	0.866	302.352
13	56	55	81	23	32	69	18	60	33	4.27	-0.266	220.848
14	93	42	50	29	92	24	88	95	55	5.68	1.363	338.136
15	37	58	41	68	64	21	63	85	18	4.55	0.058	244.176
16	13	89	67	33	18	17	26	64	86	4.13	-0.427	209.256
17	52	24	71	71	88	05	98	93	42	5.44	1.085	318.152
18	67	24	80	90	82	72	58	79	30	5.82	1.524	349.746
19	00	89	68	87	84	16	27	58	99	5.28	0.900	304.849
20	95	28	94	37	75	78	02	52	45	5.06	0.647	286.559
21	24	24	99	33	34	68	39	35	91	4.47	-0.035	237.506
22	64	11	38	67	76	77	39	75	26	4.73	0.266	259.122
23	27	25	66	64	47	53	80	70	06	4.38	-0.139	230.023
24	07	04	82	58	21	34	80	31	77	3.94	-0.647	193.441
25	51	20	12	31	19	03	16	87	11	2.5	-2.009	73.718