3.1. Вращательное движение твердого тела. Момент инерции. Теорема Штейнера

Твердыми называют тела, в которых не происходит перемещение одних частей этого тела относительно других.

Если прямая линия, проведенная через две точки этого тела, остается параллельной самой себе, то такое движение твердого тела называют поступательным.

При вращательном движении все точки тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения. При вращательном движении мерой инерции служит понятие момент инерции J . Если вращающееся тело можно принять за материальную точку, то

J = mr² , (3.1)

где r – кратчайшее расстояние от материальной точки до оси вращения.

Чтобы определить момент инерции тела относительно выделенной оси вращения, необходимо это тело разбить на отдельные материальные точки. Для произвольной материальной точки этого тела J_i = dm_ir_i ² .Сложение же моментов инерций отдельных точек этого тела позволяет определить момент инерции всего тела относительно выделенной оси:

_{. (3.2)}

_{Используя интегрирование, для однородных симметричных тел, оси вращения у которых проходят через центр масс этого тела, момент инерции можно выразит с помощью приведенные ниже формул.}

1. _{Сплошной однородный диск (или цилиндр) массой m, радиусом R (рис. 3.1а):}

_{. (3.3)}

2. _{Однородный шар с массой m и радиусом R (рис. 3.1б):}

_{. (3.4)}

3. _{Тонкий однородный стержень массой m и длиной l (рис. 3.1в):}

_{. (3.5)}

_{Для расчета момента инерции тела относительно произвольной оси вращения можно воспользоваться формулой теоремы Штейнера}

_{, (3.6)}

где _{и - моменты инерции тела относительно двух осей – оси проходящей через центр масс}

_{тела ( ) и параллельной ей оси ( ), отстоящей от нее на расстояние a (рис. 3.1г).}

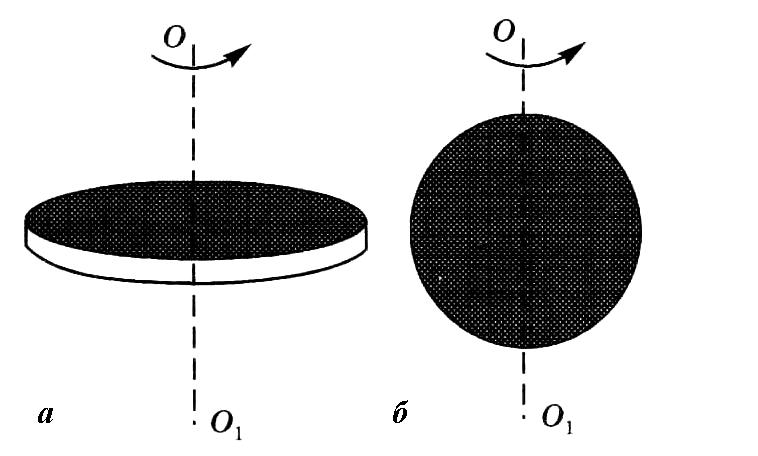
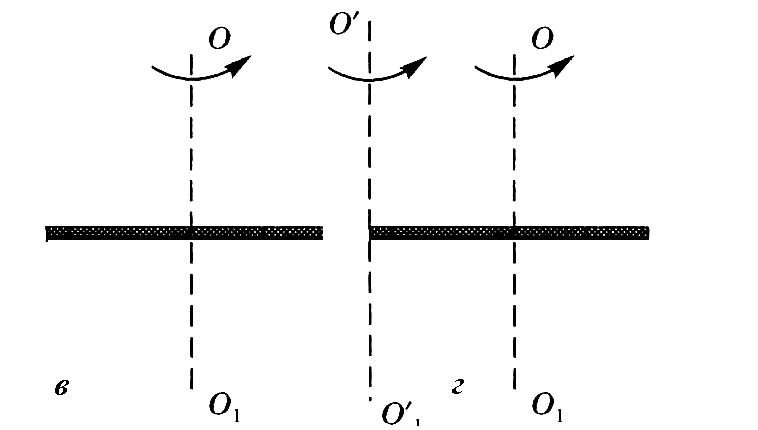
Рис. 3.1

_{Так для О',О1 , проходящей через один из концов тонкого стержня (рис. 3.1г), можно получить}

3.2. Кинетическая энергия вращающегося твердого тела

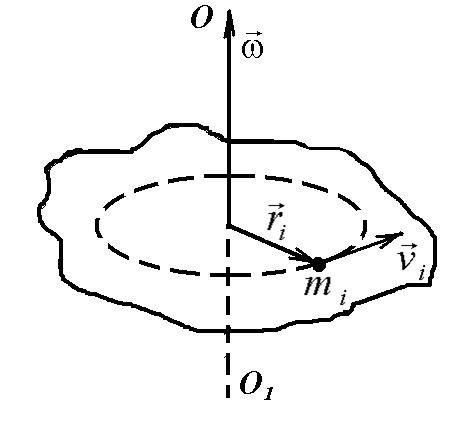
_{Определим выражение кинетической энергии для тела, вращающегося вокруг выделенной оси (рис. 3.2). Разобьем тело на отдельные материальные точки. Для каждой из материальных точек можно записать выражение}

_{. Так как , то}

_г

Рис. 3.2

де _и

Энергия вращательного движения тела

_(3.8)

_где

_{В том случае, когда тело совершает не только поступательное, но и вращательное движение полная кинетическая энергия}

3.3. Основное уравнение динамики вращательного движения

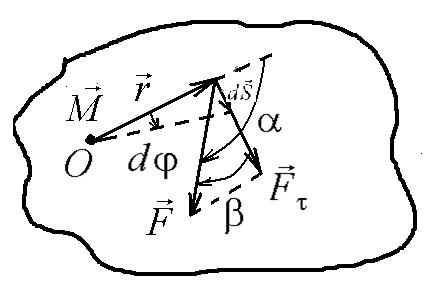
_{Если тело, закрепленное на неподвижной оси О, приходит во вращательное движение под действием некоторой силы (рис. 3.3), то эта сила совершает над телом работу. Работа силы приводит к приращению кинетической энергии (dA = dT).}

_Т

Рис. 3.3

ак как _{, а}

_{то где - момент силы.}

_{Модуль момента силы . Направление вектора определяется по правилу правого винта (см. приложение 1). На рис. 3.3 момент силы направлен по оси вращения от нас.}

_{Так как то Взяв производную по времени от последнего выражения, получим:}

_{или . (3.9)}

_{Записанное соотношение и называют основным уравнением динамики вращательного движения. В динамике вращательного движения используется понятие момент импульса}

_{Используя это понятие основное уравнение динамики вращательного движения можно записать в виде:}

_(3.10)

_{Из последнего выражения следует, что при , - закон сохранения момента импульса.}

_{Основные уравнения динамики поступательного и вращательного движений можно записать, используя следующие формулы:}

_{поступательное движение вращательное движение}

_{, ,}