
- •Часть 1. Механика. Электричество и магнетизм. Колебания
- •1.1. Механика. Материальная точка. Движение материальной точки. Скорость и ускорение произвольно движущейся точки
- •1.2. Кинематика вращательного движения
- •1.3. Динамика движения материальной точки. Законы Ньютона
- •2.1. Закон всемирного тяготения. Сила тяготения, сила тяжести, вес тела
- •2.2. Неинерциальные системы отсчета. Силы инерции
- •2.3. Центр масс. Закон сохранения импульса
- •2.4. Кинетическая энергия. Работа. Мощность
- •2.5. Потенциальная энергия
- •3.1. Вращательное движение твердого тела. Момент инерции. Теорема Штейнера
- •3.2. Кинетическая энергия вращающегося твердого тела
- •3.3. Основное уравнение динамики вращательного движения
- •3.4. Силы трения. Статическое и кинематическое трение
- •Кинематическое трение
- •4.1. Условие неразрывности потока жидкости
- •4.2. Уравнение Бернулли
- •4.3. Сила внутреннего трения
- •4.4. Ламинарное и турбулентное течение
- •4.5. Преобразования Галилея. Принцип относительности Галилея
- •4.6. Специальная теория относительности. Постулаты Эйнштейна. Преобразования Лоренца
- •Никакими физическими опытами, находясь внутри исо, нельзя установить, движется она равномерно и прямолинейно или покоится;
- •Все законы физики выглядят, записываются одинаково во всех исо;
- •Все физические явления протекают одинаково во всех исо;
- •5.1. Следствия из преобразований Лоренца
- •5.2. Релятивистские выражения массы и импульса тела
- •5.3. Релятивистское выражение для энергии
- •6.1. Электрические заряды. Закон Кулона
- •6.2. Потенциальная энергия. Потенциал. Работа сил электрического поля
- •6.3. Напряженность поля. Принцип суперпозиции полей
- •6.4. Связь между потенциалом и напряженностью
- •6.5. Графическое изображение электростатических полей
- •7.1. Поток и циркуляция вектора электростатического поля.
- •7 .2. Применение теоремы Гаусса для расчета электростатических полей
- •7.3. Электрическое поле в диэлектрике
- •8.1. Поле заряженного проводника
- •8.2. Электроемкость уединенного проводника. Электроемкость конденсатора
- •8.3. Энергия заряженного тела, конденсатора. Энергия электрического поля
- •8.4. Сила и плотность тока. Законы Ома и Джоуля – Ленца
- •8.5. Электродвижущая сила. Закон Ома для неоднородного участка цепи
- •8.6. Правила Кирхгофа
- •9.1. Магнитное поле. Закон Био – Савара – Лапласа
- •9.2. Сила Лоренца. Закон Ампера
- •9.3. Теорема о циркуляции вектора магнитной индукции и теорема Гаусса для вектора
- •9.4. Магнитное поле в веществе
- •10.1. Опыты Фарадея. Явление электромагнитной индукции
- •10.2. Токи Фуко
- •10.3. Явления самоиндукции и взаимоиндукции
- •10.4. Второе уравнение Максвелла в интегральной форма. Ток смещения
- •10.5. Уравнения Максвелла
- •11.1. Гармонические колебания
- •11.2. Сложение гармонических колебаний
- •1. Сложение гармонических колебаний одного направления и одинаковой частоты
- •3. Сложение взаимно перпендикулярных колебаний.
- •12.1. Затухающие колебания
- •12.2. Вынужденные колебания
- •12.3. Вынужденные колебания в цепи переменного тока
- •12.4. Мощность в цепи переменного тока
- •1. Векторы и скаляры
- •3. Циркуляция и поток вектора .
- •Библиографический список
2.1. Закон всемирного тяготения. Сила тяготения, сила тяжести, вес тела
Ньютон установил закон всемирного тяготения – материальные точки притягиваются друг друга с силой F пропорциональной их массам m1 и m2 и обратно пропорциональной квадрату расстояния r между ними:
![]() . (2.1)
. (2.1)
Коэффициент G = 6,67 × 10-11Н·м2/кг2 был определен экспериментально и назван гравитационной постоянной.
Силу, с которой Земля притягивает тела, находящиеся на поверхности Земли или близи ее поверхности, определяющую выражением
![]() ;
;
![]() , (2.2)
, (2.2)
называют силой тяжести. В формуле (2.2) m – масса тела, М – масса Земли, R – радиус Земли, g – ускорение свободного падения.
Сила, с которой тело действует на подвес или опору, называют весом тела.
2.2. Неинерциальные системы отсчета. Силы инерции
Законы Ньютона выполняются только в
инерциальных системах отсчета. Системы
отсчета, которые движутся ускоренно
относительно инерциальных систем,
называют неинерциальными. В
неинерциальной системе отсчета
ускорение тела
![]() отличается
от ускорения
в
инерциальной системе на величину
отличается
от ускорения
в
инерциальной системе на величину
![]() :
:
–
![]() =
.
=
.
Пусть результирующая всех сил,
обусловленных действием на данное тело
со стороны других тел, равна
![]() ,
тогда согласно второму закону Ньютона
ускорение тела относительно любой
инерциальной системы отсчета равно
,
тогда согласно второму закону Ньютона
ускорение тела относительно любой
инерциальной системы отсчета равно
![]() .
.
Ускорение же тела относительно неинерциальной системы можно представить в виде
=
–
=
![]() .
.
Отсюда следует, что при = 0 тело будет двигаться по отношению к неинерциальной системе отсчета с ускорением , т. е. так, как если бы на него действовала сила, равная – m .
Сказанное означает, что при описании
движения в неинерциальных системах
можно пользоваться уравнениями движения
Ньютона, если наряду с силами воздействия
тел друг на друга, учитывать так называемые
силы инерции![]() .
Силы инерции следует полагать равными
произведению массы тела на взятую с
обратным знаком разность его ускорений
по отношению к инерциальной и неинерциальной
систем отсчета:
.
Силы инерции следует полагать равными
произведению массы тела на взятую с
обратным знаком разность его ускорений
по отношению к инерциальной и неинерциальной
систем отсчета:
![]() .
.
Следовательно, уравнение движения в неинерциальной системе отсчета будет иметь вид:
![]() . (2.3)
. (2.3)
Поясним наше утверждение примерами.
1
Рис. 2.1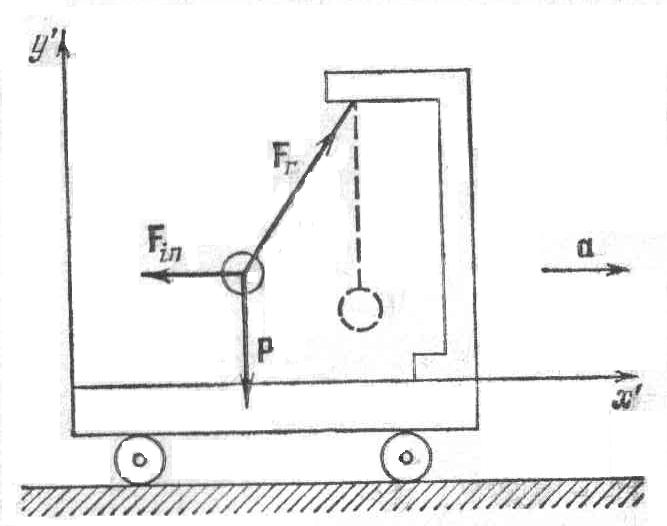
![]() .
Нить отклонится от вертикали на такой
угол, чтобы результирующая сил
.
Нить отклонится от вертикали на такой
угол, чтобы результирующая сил
![]() и
и
![]() сообщала шарику ускорение
.
Относительно системы отсчета, связанной
с тележкой, шарик покоится, несмотря на
то, что результирующая сил
сообщала шарику ускорение
.
Относительно системы отсчета, связанной
с тележкой, шарик покоится, несмотря на
то, что результирующая сил
![]() и
отлична
от нуля. Отсутствие ускорения шарика
по отношению к этой
и
отлична
от нуля. Отсутствие ускорения шарика
по отношению к этой
системе отсчета можно формально
объяснить тем, что, кроме сил
и
на
шарик действует и сила инерции
![]() .
.
Следовательно, в неинерциальной системе отсчета при ускоренном прямолинейном движении этой системы на тела неподвижные относительно этой системы действует сила инерции
![]() . (2.4)
. (2.4)
2
Рис. 2.2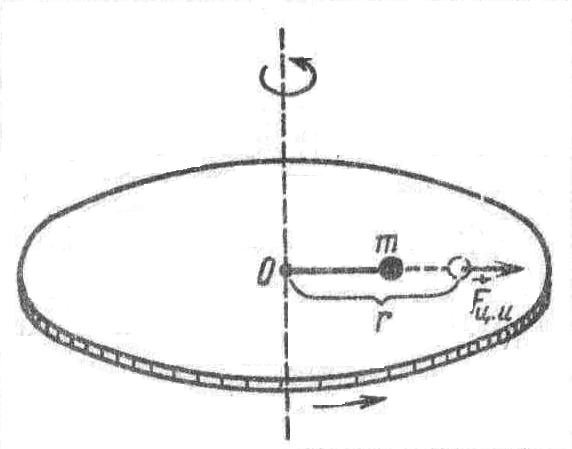
![]() (и, следовательно, превратится в
неинерциальную систему отсчета), то
благодаря трению тело тоже будет
вовлечено во вращение. Вместе с тем оно
будет перемещаться в радиальном
направлении от центра платформы до тех
пор, пока возвращающая сила упругости
не остановит это перемещение. Тогда
тело начнет вращаться на расстоянии r
от центра О. С точки зрения
наблюдателя, связанного с платформой,
перемещение
(и, следовательно, превратится в
неинерциальную систему отсчета), то
благодаря трению тело тоже будет
вовлечено во вращение. Вместе с тем оно
будет перемещаться в радиальном
направлении от центра платформы до тех
пор, пока возвращающая сила упругости
не остановит это перемещение. Тогда
тело начнет вращаться на расстоянии r
от центра О. С точки зрения
наблюдателя, связанного с платформой,
перемещение
шара относительно нее обусловлено
некоторой силой
![]() .
Это сила инерции, поскольку она не
вызвана действием на шар других
определенных сил; ее называют центробежной
силой инерции. Очевидно, что
центробежная сила инерции равна по
модулю и противоположна по направлению
центростремительной силе, действующей
на тело.
.
Это сила инерции, поскольку она не
вызвана действием на шар других
определенных сил; ее называют центробежной
силой инерции. Очевидно, что
центробежная сила инерции равна по
модулю и противоположна по направлению
центростремительной силе, действующей
на тело.
Поэтому
![]() . (2.5)
. (2.5)
