1.2. Кинематика вращательного движения

_{Пусть м. т. движется со скоростью по окружности радиуса r вокруг неподвижной оси вращения (рис.1.4а). Положение точки на окружности определяет радиус-вектор , а вектор} его элементарного приращения _{направлен по касательной к окружности. Введем понятие вектора элементарного углового перемещения : он равен по модулю углу элементарного поворота dφ, направлен по оси вращения и связан с направлением вращения правилом правого буравчика, а именно: направление вращения буравчика должно совпадать с направлением вращения материальной точки, тогда поступательное движение буравчика определяет направление вектора (рис. 1.4а).}

Рис. 1.4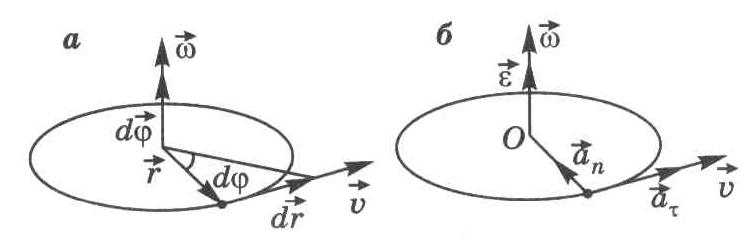

_{Быстроту вращения м. т. характеризует угловая скорость , равная первой производной от вектора углового перемещения по времени t:}

_(1.6)

_{Направление вектора угловой скорости и вектора элементарного углового перемещения совпадают.}

_{Быстроту изменения угловой скорости характеризует вектор углового ускорения , равный первой производной от угловой скорости по времени t:}

_(1.7)

_{Кроме перечисленных выше величин, для описания вращательного движения тела используют частоту вращения n, определяемую как число оборотов, совершенных телом за единицу времени, и период обращения Т, как время одного полного оборота. Справедлива следующая взаимосвязь ω, n и Т:}

_{ω = 2πn = 2π/Т. (1.8)}

_{Установим взаимосвязь линейных} ( _{, ) и угловых ( , ) характеристик при вращательном движении.}

_{Пользуясь определением векторного произведения двух векторов (см. Прил. 1) и рис. 1.4а, можно записать}

_(1.9)

_{Выражение (1.9) позволяет получить следующие формулы взаимосвязи линейных и угловых характеристик:}

1. _{для скоростей и}

_{; v = ωr . (1.10)}

2. для ускорений _{, ,}

_;

_{; aτ = εr , (1.11)}

_{, an = ων =ν}²_{/r = ω}²_{r. (1.12)}

1.3. Динамика движения материальной точки. Законы Ньютона

Динамика изучает движение тел в связи с теми причинами (взаимодействиями между телами), которые обуславливают тот или иной характер движения. Механическое взаимодействие тела с другими телами описывают с помощью понятия силы , которая определяется как векторная величина, характеризующая механическое взаимодействие данного тела с другими телами, приводящая к их деформации или к возникновению ускорения.

Все тела изменяют свою скорость не мгновенно, а постепенно при их взаимодействии с другими телами, то есть обладают инертностью. Количественной характеристикой инертности тела является его масса m. Она определяется как мера инертности тела при его прямолинейном движении.

В основе классической механики движения материальной точки лежат три закона Ньютона, являющиеся обобщением опытных фактов.

1 закон Ньютона рассматривает движение тела в отсутствии его взаимодействия с другими телами. Тело покоится или движется равномерно и прямолинейно, если на тело не действуют другие тела или их действие скомпенсировано.

Оказывается, что законы Ньютона выполняется не во всех системах отсчета, а только в инерциальных. Поэтому среди всех систем отсчета выделяют инерциальные системы отсчет (ИСО), как системы отсчета, в которых выполняются все три закона Ньютона.

ИСО в природе не существует, так как тела отсчета либо вращаются, либо движутся прямолинейно с ускорением. Наиболее близкой к ИСО можно считать систему отсчета связанную с Солнцем. Для многих физических явлений систему отсчета, связанную с Землей, также можно считать ИСО. Системы отсчета, которые движутся прямолинейно и равномерно относительно инерциальных систем, так же являются инерциальными системами.

Для формулировки второго закона Ньютон ввел понятие импульса тела _{как векторную физическую величину, характеризующую его прямолинейное движение и равную произведению массы тела на его скорость:}

_{. (1.13)}

_{Согласно второго закона Ньютона первая производная от импульса тела по времени t равна векторной сумме сил, действующих на тело:}

_{. (1.14)}

_{Если масса тела не изменяется от времени}, то тогда выражение (1.14) можно записать, вводя в него ускорение тела:

_{, (1.15)}

_{и сформулировать второй закон Ньютона следующим образом: произведение массы тела на его ускорение равно векторной сумме сил, действующих на тело.}

_{Третий закон Ньютона устанавливает дополнительные связи между силами, возникающими при взаимодействии тел. Согласно этому закону силы, действующие между двумя талами равны по модулю и противоположны по направлению:}

_{. (1.16)}

Лекция 2