12.1. Затухающие колебания

Затухающие колебания наблюдаются в замкнутой механической системе (F_внеш = 0), в которой имеются потери энергии на преодоление сил сопротивления, или в закрытом колебательном контуре (U_внеш = 0), в котором наличие сопротивления R приводит к потере энергии колебаний из-за нагревания проводников. В первом приближении можно считать, что при небольших скоростях движения, силы, вызывающие затухание механических колебаний, пропорциональны величине скорости. Будем называть эти силы, независимо от их происхождения, силами трения, или сопротивления:

_,

_{где r – коэффициент сопротивления. Знак минус указывает, что сила трения всегда направлена в сторону, противоположную направлению движения.}

_{Запишем второй закон Ньютона для затухающих колебаний тела вдоль оси ОХ:}

_{max = - kx - rvx .}

_{Заменив и перенеся все члены в левую часть уравнения, получим}

_(12.1)

_{где - коэффициент затухания.}

_{Если β ≤ ω0, то в результате решения дифференциального уравнения (12.1) получается следующая зависимость смещения от времени:}

_{, (12.2)}

_{где е – основание натуральных логарифмов.}

_{Выражение}

_(12.3)

_{называют амплитудой затухающих колебаний.}

_{Величину}

_(12.4)

_{называют собственной циклической частотой затухающих колебаний.}

_{Затухающие колебания представляют собой непериодические колебания, так как в них никогда не повторяются, например, максимальные значения смещения, скорости и ускорения. Поэтому называть ωз циклической частотой можно лишь условно. По этой же причине}

_{, (12.5)}

_{обычно называемую периодом затухающих колебаний, правильнее называть условным периодом затухающих колебаний.}

_{Отношение амплитуд для моментов времени, отличающихся на период, равно}

_{. (12.6)}

_{Э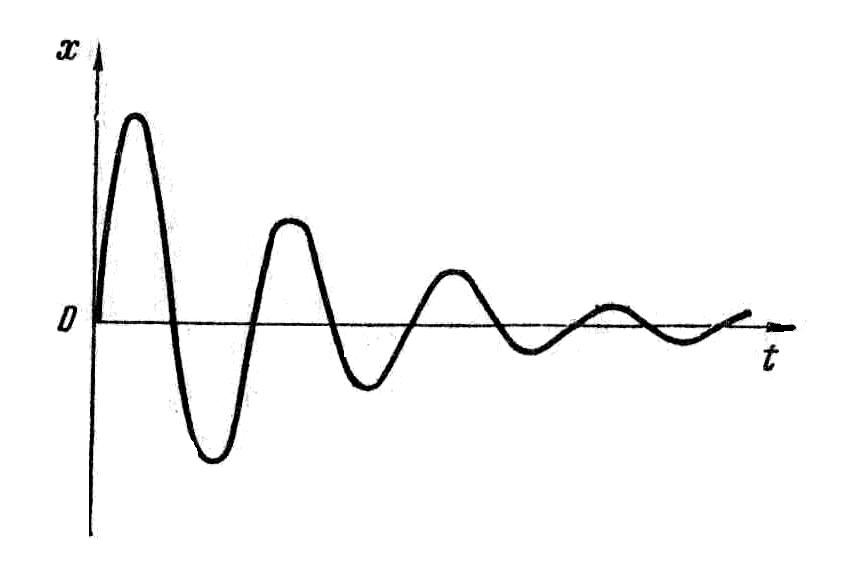 то отношение называют декрементом затухания, а его логарифм – логарифмическим декрементом затухания:}

_{. (12.7)}

_{На рис.12.1 дан график функции} (12.2).

Рис. 12.1.

12.2. Вынужденные колебания

Под вынужденными колебаниями понимают колебания, происходящие в системе в результате внешнего воздействия (внешней силы или внешнего напряжения), изменяющегося со временем по гармоническому закону. В этом случае колебания описываются дифференциальным уравнением

_{, (12.8)}

_{где - вынуждающая сила, ω – частота силы.}

Известно, что решением этого уравнения (12.8) является следующее выражение:

_{. (12.9)}

_{Первое слагаемое представляет собой уравнение свободных затухающих колебаний системы. Амплитуда этих колебаний с течением времени уменьшается. Для установившихся колебаний первое слагаемое уравнения (12.9) равно нулю и}

_{. (12.10)}

_{Амплитуда вынужденных установившихся колебаний}

_(12.11)

_з

Рис. 12.2.

ависит как от частоты _{ω вынуждающей силы, так и от параметров системы (m, k, r).}

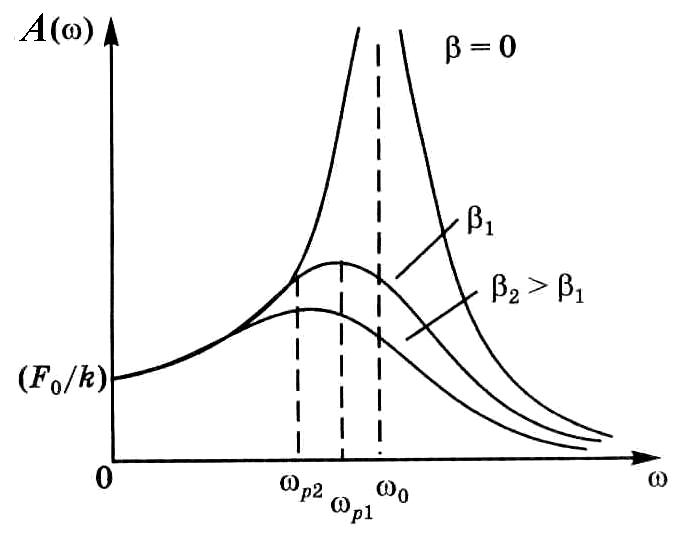
Графики зависимостей А от ω для различных значений коэффициента затухания β приведены на рис. 12.2.

Явление, при котором наблюдается резкое возрастание амплитуды вынужденных колебаний при приближении частоты внешнего воздействия к частоте собственных свободных незатухающих колебаний системы, называют резонансом. Частоты, при которых амплитуда вынужденных установившихся колебаний принимает максимальное значение, называют резонансными ω_р.

Найдем ω_р при которой амплитуда имеет максимальное значение. Резонанс наблюдается в том случае, когда выражение под знаком квадратного корня в формуле (12.11) будет минимальным. Поэтому

_{. (12.12)}