10.2. Токи Фуко

_{Токи Фуко – это индукционные токи, возникающие в массивных проводниках. Для таких проводников сопротивление R будет мало, и по этому индукционные токи (Ii = εi/R) достигают большой величины. Их можно использовать для нагревания и плавления металлических заготовок, демпфирования подвижных частей электроприборов.}

_{Токи Фуко могут приводить и к нежелательным явлениям – нагреву сердечников трансформаторов, электродвигателей и т. д. Поэтому сопротивление массивного проводника увеличивают, набирая его в виде отдельных пластин, и тем самым уменьшают нагрев проводников.}

_{Нужно также отметить, что возникновение индукционного тока при пропускании по проводнику переменного тока приводит к перераспределению суммарного тока по сечению проводника, а именно он вытесняется на поверхность проводника (скин-эффект).}

_{Явление скин-эффекта наиболее заметно в СВЧ-диапазоне (диапазон сверх высоких частот ν ~ 10}¹⁰ _{Гц), в этом случае переменный ток течет в слое малой толщины в близи поверхности проводника.}

Рис. 10.3

Дадим краткое объяснение этому явлению. Рассмотрим текущий по проводнику переменный ток проводимости в тот момент времени, когда вектор напряженности _{внешнего электрического поля направлен вверх, а сила тока и соответственно вектор магнитной индукции возрастают по модулю (рис. 10.3). Согласно первому уравнению Максвелла переменное магнитное поле создает в окружающем пространстве вихревое электрическое поле. Направление линий этого поля показано на рис. 10.3. Как видно из рисунка, около осевой линии проводника в его центральной части линии и направлены в противоположные стороны, а в близи поверхности проводника – в одну сторону. Это и приводит к ослаблению плотности тока в центральной части и его возрастанию около поверхности проводника.}

10.3. Явления самоиндукции и взаимоиндукции

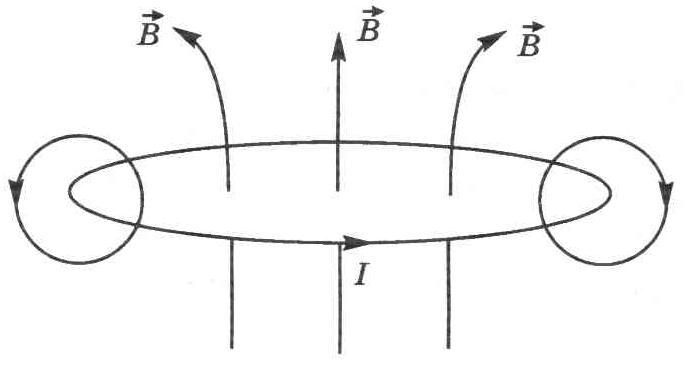
Рис. 10.4

Возьмем контур, по которому протекает ток _{I . Он создает в окружающем пространстве магнитное поле, линии которого пронизывают плоскость контура (рис.10.4). Возникающий при этом поток получил название магнитного потока самоиндукции ФS, так как сам ток индуцирует этот магнитный поток. Под явлением самоиндукции можно понимать возникновение магнитного}

_{потока самоиндукции при протекании по цепи тока. В случае, когда контур содержит N витков, используется понятие потокосцепления ψS самоиндукции (ψS = NФS). Оказывается, что ψS и I прямо пропорциональны друг другу и поэтому можно записать}

_{ψS = LI,}

_{где коэффициент пропорциональности L называют индуктивностью контура. Он описывает способность контура создавать потокосцепление самоиндукции и равен отношению ψS и I:}

_.

_{Индуктивность контура зависит от геометрических размеров контура и от магнитных свойств среды.}

_{Самоиндукцией называют также явление возникновения ЭДС индукции в том контуре, по которому протекает} переменный ток. Возникающие при этом ЭДС индукции

_{εi и индуктивный ток II называют ЭДС самоиндукции εS и током самоиндукции IS. Для них можно записать}

_{. (10.6)}

_{Из формулы (10.6) следует, что любое изменение тока в цепи тормозится, и тем сильнее, чем больше индуктивность цепи и меньше ее сопротивление.}

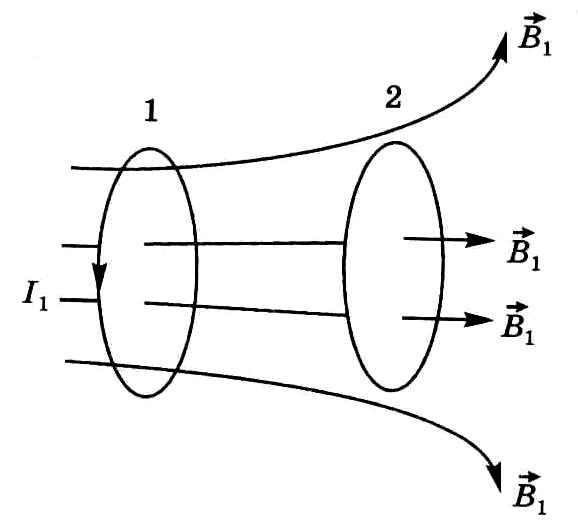
Рис. 10.5

Пусть в пространстве находится два проводящих контура 1 и 2 (рис. 10.5). Если пропустить по контуру 1 ток _{I1, то часть линий вектора магнитной индукции , созданного током I1 магнитного поля, будет пересекать плоскость второго контура. вследствие чего возникает потокосцепление ψ21 взаимной индукции, которое прямо пропорционально силе тока I1:}

_{ψ21 = L21I1. (10.7)}

_{Если пропустить ток I2 по второму контуру, то аналогичные рассуждения приведут к следующей формуле:}

_{Ψ12 = L12I2. (10.8)}

_{Можно показать, что в случае неферромагнитной среды входящие в формулы (10.7) и (10.8) коэффициенты пропорциональности L12 и L21 будут одинаковыми, они получили название взаимной индуктивности контуров 1 и 2:}

_{L12 = L21 = Ψ12/I2 = ψ21/I1. (10.9)}

_{Взаимная индуктивность зависит от расположения контуров, их геометрии и магнитных свойств окружающей среды.}

_{Явление взаимной индукции – это явление возникновения ЭДС индукции в одном контуре при протекании переменного тока в другом контуре. Используя закон Фарадея можно записать:}

_(10.10)

_{На явлении взаимной индукции основан принцип действия трансформаторов, применяемых для повышения или понижения напряжения переменного тока.}