9.2. Сила Лоренца. Закон Ампера

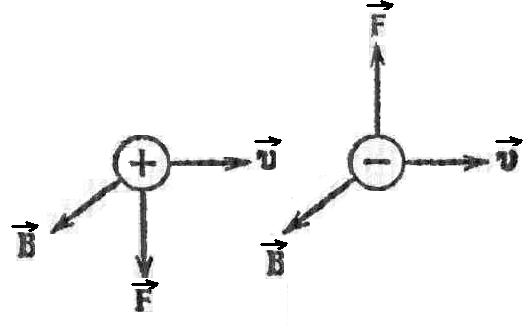
_{На заряд, движущийся в магнитном поле, действует сила, которую мы будем называть магнитной. Эта сила определяется зарядом q, скоростью его движения и магнитной индукцией в той точке, где находится заряд в рассматриваемый момент времени. Опытным путем установлено, что сила , действующая на заряд, движущейся в магнитном поле, определяется формулой}

_(9.4)

_{Модуль магнитной силы равен}

где α – угол между векторами _{и .}

Рис. 9.3

Направлена магнитная сила перпендикулярно плоскости, в которой лежат векторы _{и . Если заряд q положителен, направление силы совпадает с направлением вектора В случае отрицательного q направления и противоположны (рис. 9.3).}

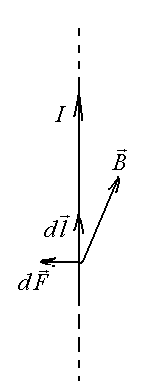_{Если имеются одновременно электрическое и магнитное поля, сила, действующая на заряженную частицу, равна}

_{. (9.5)}

_{Это выражение было получено из опытов Лоренца и носит название силы Лоренца.}

_{Если провод, по которому течет ток, находится в магнитном поле, на каждый из носителей тока, а, следовательно, на проводник действует магнитная сила. Опытным путем установлено, что на элемент проводника длиной с током в магнитном поле действует сила}

Рис. 9.4

_{, (9.10)}

_{получившая название силы Ампера. Модуль этой силы вычисляется по формуле}

_,

_{где α – угол между векторами и (рис. 9.4).}

9.3. Теорема о циркуляции вектора магнитной индукции и теорема Гаусса для вектора

_{Можно доказать теорему о циркуляции вектора для вакуума: циркуляция вектора по произвольному замкнутому контуру Г равна алгебраической сумме токов, охватываемых этим контуром, умноженной на :}

_{. (9.11)}

_{Знак силы тока в формуле (9.11) выбирается следующим образом: если направление тока связано с направлением обхода контура правилом правого буравчика, то это «+», если нет – «-».}

_{В присутствии вещества в правую часть теоремы о циркуляции вектора необходимо ввести микротоки Iмикро, охватываемые контуром Г:}

_{, (9.12)}

_{где μ – относительная магнитная проницаемость среды.}

_{Под микротоками, или молекулярными токами, понимают токи, вызванные движением электронов в молекулах. Эти токи создают магнитное поле вещества, помещенного во внешнем магнитном поле.}

_{Из формулы (9.12) следует физический смысл теоремы о циркуляции вектора , а именно источником магнитного поля являются токи проводимости и микротоки. В природе не существует магнитных зарядов, поэтому линии являются замкнутыми.}

Магнитное поле в отличие от электростатического – непотенциальное поле: циркуляция вектора _{магнитной индукции вдоль замкнутого контура, вообще говоря, не равна нулю и зависит от выбора контура. Такое поле называют вихревым или соленоидальным.}

_{Так как в природе нет магнитных зарядов, линии являются замкнутыми, теорему Гаусса для вектора магнитной индукции запишем следующим образом:}

_.

9.4. Магнитное поле в веществе

_{Все вещества являются магнетиками – при помещении их во внешнее магнитное поле они создают свое магнитное поле , то есть намагничиваются:}

Рис. 9.5

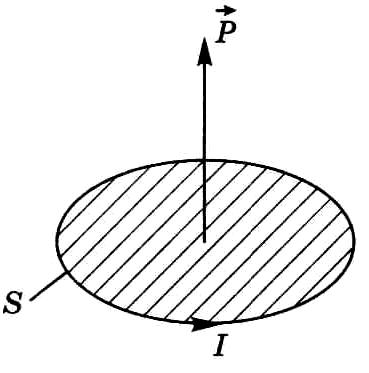
Качественно возникновение собственного магнитного поля _{магнетика можно пояснить на основе гипотезы Ампера существовании внутри молекул молекулярных токов (микротоков). Произведение кругового тока на обтекаемую им площадь называют магнитным моментом (рис. 9.5) . Модуль вектора Для характеристики магнетика вводят вектор намагничивания , который равен векторной сумме магнитных моментов атомов, находящихся в единице объема вещества:}

_{Ориентация магнитных моментов атомов во внешнем магнитном поле и создает не равное нулю магнитное поле вещества и соответственно (рис. 9.6).}

Рис. 9.6

_{Для удобства описания магнитных полей в среде вводится вектор напряженности магнитного поля}

_{В случае вакуума = 0, и поэтому}

_{Для однородных изотропных магнетиков из опыта установлена следующая формула связи векторов и :}

_{где χ – магнитная восприимчивость вещества.}

_{Для векторов и в случае однородного и изотропного магнетика с учетом выше приведенных формул получаются следующие выражения:}

_{Теорему о циркуляции вектора по произвольному замкнутому контуру Г можно представить в виде}

_{По магнитным свойствам вещества можно разбить на три группы: диамагнетики, парамагнетики и ферромагнетики.}

_{Диамагнетиками называются вещества, магнитные моменты атомов или молекул которых при отсутствии внешнего магнитного поля равны нулю. При внесении диамагнитного вещества в магнитное поле в каждом атоме наводится магнитный момент направленный противоположно вектору магнитной индукции поля. Для диамагнитных веществ χ < 0 и μ < 1.}

_{У парамагнитных веществ магнитные моменты атомов или молекул при отсутствии внешнего магнитного поля не равны нулю. При внесении парамагнетика в магнитное поле магнитные моменты атомов стремятся сориентироваться по направлению этого поля. Для парамагнитных веществ χ > 0 и μ > 1. Эксперименты указывают, что μ пара- и диамагнитных веществ незначительно отличаются от единицы.}

_{Ферромагнитными веществами называют такие вещества, в которых внутреннее магнитное поле в сотни и тысячи раз превышает вызвавшее его внешнее поле.}

_{Объемная плотность энергии магнитного поля в неферромагнитной среда равна}

Лекция 10