8.3. Энергия заряженного тела, конденсатора. Энергия электрического поля

_{Выведем формулу для энергии заряженного проводника. Рассмотрим работу внешних сил по увеличению заряда проводника от q1 = 0 до q2. Для этого будем малыми порциями dq перемещать заряд из бесконечности на поверхность проводника. При этом работа внешней силы будет совершаться против кулоновской силы отталкивания одноименных зарядов и поэтому}

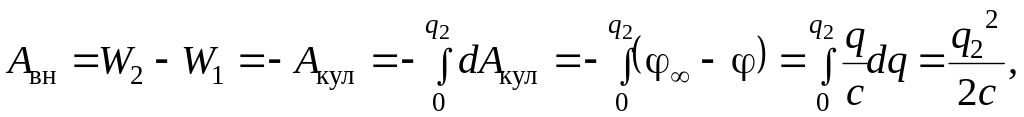
_{где учтено, что W1 = 0.}

_{Учитывая, что q = cφ, для энергии заряженного уединенного проводника можно записать}

_(8.8)

_{Аналогично рассуждая, можно получить формулу для энергии заряженного конденсатора.}

_(8.9)

_{Преобразовав формулу (8.9), для энергии заряженного плоского конденсатора получим}

_{где V = Sd – объем пространства между обкладками конденсатора, w – объемная плотность электростатического поля.}

_{Введение w позволяет рассчитать энергию W электростатического поля в любом конечном объеме пространства:}

8.4. Сила и плотность тока. Законы Ома и Джоуля – Ленца

_{Под электрическим током понимают упорядоченное движение заряженных частиц. Электрический ток существует при наличии свободных зарядов и электрического поля.}

_{Протекающий по проводнику ток характеризует сила тока I, определяемая по формуле}

_{где dq – заряд, проходящий через поперечное сечение проводника за единицу времени. Распределение тока по сечению проводника характеризует вектор плотности тока , направление которого в каждой точке проводника совпадает с направлением скорости}

_{упорядоченных положительных частиц. Модуль вектора равен}

_{где dI – сила тока, протекающего в данной точке внутри проводника через элементарную площадку , расположенную перпендикулярно к направлению тока.}

_{Введение вектора плотности тока позволяет найти силу тока, протекающего через любую поверхность S:}

_{Вектор плотности тока где q0 – заряд свободной заряженной частицы, - средняя скорость направленного движения заряженной частицы.}

_{Г. Ом экспериментально установил следующий закон: сила тока I, текущего по однородному участку цепи, прямо пропорциональна напряжению U , приложенному к нему и обратно пропорциональна сопротивлению R этого участка цепи:}

_{Однородным участком электрической цепи называют участок, на котором направленное движение зарядов происходит под действием только кулоновских сил. Отметим, что для однородного участка цепи напряжение U совпадает с разностью потенциалов φ1 – φ2 между начальной и конечной точками участка.}

_{Закон Джоуля - Ленца формулируется следующим образом: количество теплоты, выделяемое в проводнике при протекании по нему электрического тока, равно произведению квадрата силы тока на сопротивление проводника и на время протекания по нему тока:}

_{Учитывая, что , законы Ома и Джоуля – Ленца можно записать в дифференциальной форме:}

_{где - количество теплоты, которое выделяется в единице объема проводника за единицу времени.}

8.5. Электродвижущая сила. Закон Ома для неоднородного участка цепи

_{Возьмем замкнутую электрическую цепь, содержащую источник тока. Рассмотрим как происходит движение положительного заряда (+q) по этой цепи (рис. 8.4).}

_{Рис. 8.4}

Во внешней части цепи сопротивлением

_{R под действием кулоновских сил заряд (+q) перемещается от точек с большим потенциалом к точкам с меньшим потенциалом. Кулоновские силы только соединяют разноименные заряды, поэтому в источнике тока на заряды, кроме них, должны действовать так же и сторонние силы, совершающие работу по разделению разноименных зарядов и переводящие заряд (+q) от отрицательного полюса источника к его положительному полюсу.}

_{Источник тока можно охарактеризовать внутренним сопротивлением r и электродвижущей силой (ЭДС) ε – она определяет работу сторонних сил по перемещению точечного положительного заряда в один кулон от отрицательного полюса к его положительному полюсу:}

_{Природа сторонних сил может быть любой, от них требуется лишь способность разделять разноименные заряды. Это могут быть силы трения, силы химической реакций, протекающих в гальванических элементах, силы магнитного поля и т. д.}

_{Участок цепи, на котором одновременно действуют кулоновские и сторонние сил, называют неоднородным участком цепи. Для участка цепи, изображенного на рис. 8.5, формула закона Ома имеет вид}

Рис. 8.5