8.1. Поле заряженного проводника

К проводникам относятся вещества, проводящие электрический ток; в них имеются свободные заряды, которые способны перемещаться по проводнику под действием электрического поля. В металлических проводниках свободными зарядами являются электроны, они образуют газ, заполняющий кристаллическую решетку положительно заряженных ионов.

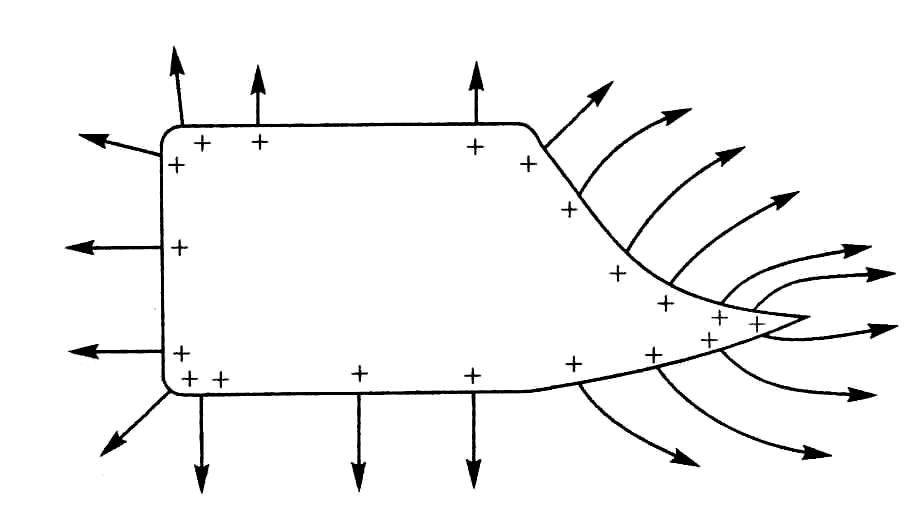
Рассмотрим, что произойдет, если проводнику сообщить избыточный заряд. В условиях равновесия избыточного заряда справедливы следующие утверждения.

1. Электрическое поле внутри проводника отсутствует, а объем проводника и его поверхность являются эквипотенциальными:

_(8.1)

_{Действительно, если равенство (8.1) не выполняется, то тогда свободные заряды в проводнике будут перемещаться, так как работа сил электростатического поля не будет равна нулю. Это противоречит условию равновесия избыточного заряда: в условиях равновесия они должны быть неподвижными.}

_{2. Избыточный заряд распределится только по внешней поверхности, так как из-за кулоновского отталкивания одноименных зарядов они стараются разойтись на максимально возможные расстояния.}

Рис. 8.1

3. Распределение избыточного заряда по внешней поверхности проводника является неравномерным: поверхностная плотность заряда _{σ больше в тех точках поверхности проводника, где ее кривизна больше (рис. 8.1).}

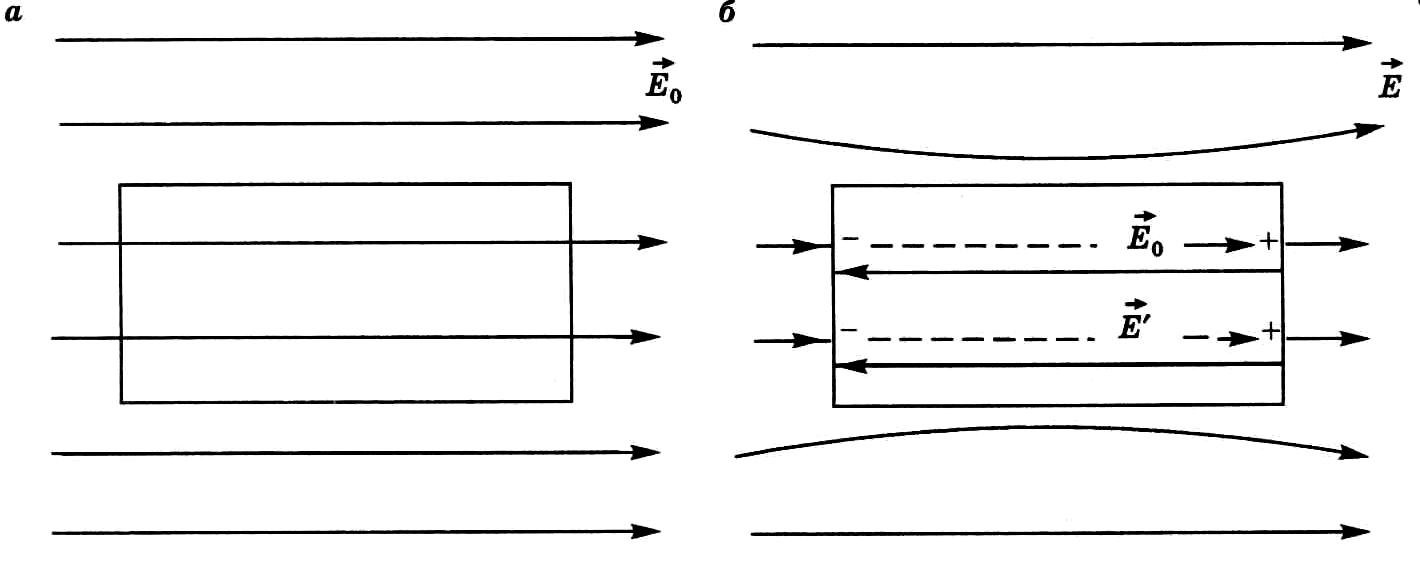
_{Если в электрическое поле напряженности поместить незаряженный проводник, то под действием сил поля свободные заряды в проводнике приходят в движение и на его противоположных сторонах появляются индуцированные заряды, которые компенсируют внешнее поле внутри проводника (рис. 8.2), и искажают внешнее поле снаружи, вблизи поверхности.}

_И

Рис. 8.2

так, внешнее электрическое поле не проникает внутрь металла. Это позволяет использовать металлическую оболочку, сплошную или в виде сетки, для защиты различных приборов от внешних электрических полей.

8.2. Электроемкость уединенного проводника. Электроемкость конденсатора

_{Рассмотрим уединенный проводник, в окружающем пространстве которого нет других тел. Из формул электростатики следует, что заряд проводника q и его потенциал φ (он в условиях равновесия одинаковый внутри и на поверхности проводника) будут пропорциональны друг другу (q = c∙φ). Поэтому коэффициент пропорциональности между ними}

_(8.2)

_{не будет зависеть ни от q ни от φ, он называется электроемкостью проводника. Электроемкость проводника характеризует его способность накапливать заряды и зависит только от геометрических размеров проводника, его формы и диэлектрических свойств окружающей среды (ε). Действительно, в случае металлической сферы можно записать:}

_(8.3)

_{Электроемкость уединенного проводника является достаточно малой величиной. Так, если рассматривать планету Земля как проводящий шар, то тогда ее электроемкость составит всего 711 мкФ. Эксперименты показывают, что приближение к проводнику каких-либо тел ведет к увеличению электроемкости этого проводника.}

_{Наибольший эффект увеличения электроемкости проводника достигается для конденсаторов, представляющих собой две металлические пластины, разделенные слоем диэлектрика. На пластины (обкладки) подают заряды, одинаковые по модулю и противоположные по знаку. Форма обкладок конденсатора обеспечивает существование электрического поля только в пространстве между ними. Это позволяет устранить влияние на электроемкость конденсатора других тел.}

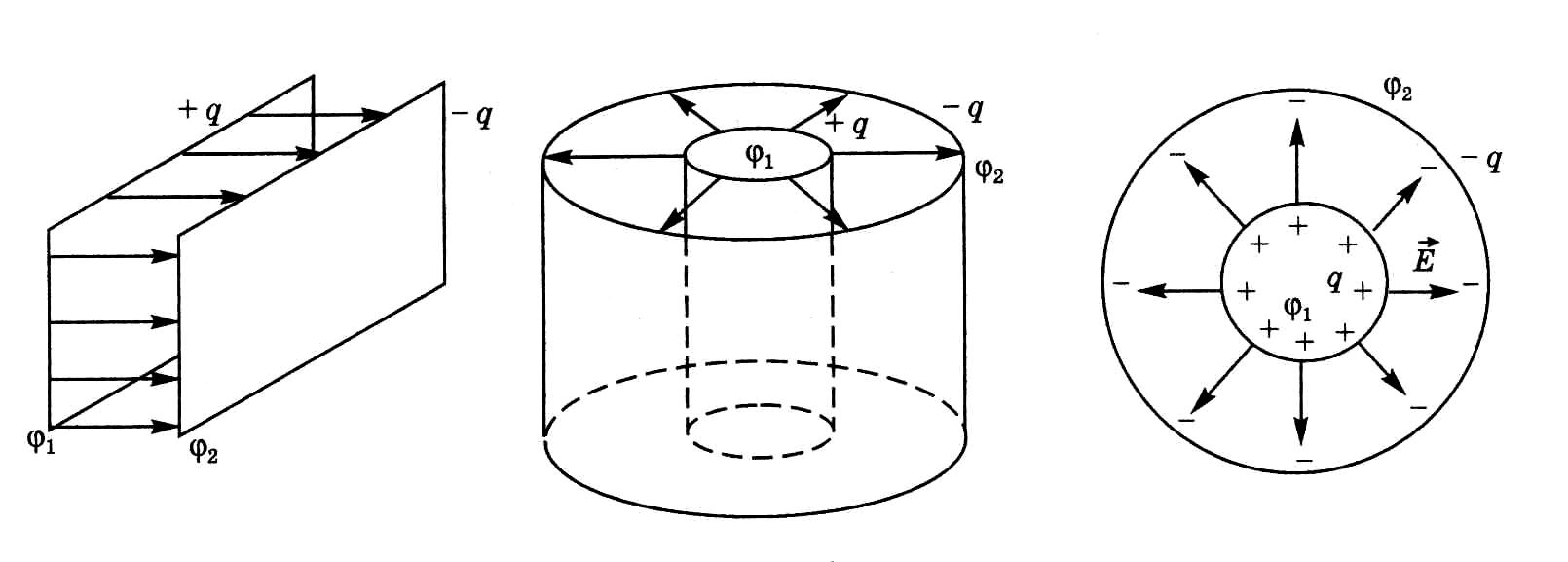
_{На рис. 8.3 приведено схематическое изображение плоского, цилиндрического и}

_с

Рис. 8.3

ферического конденсаторов.

_{Электроемкость конденсатора вводится по формуле}

_(8.4)

_{где q – заряд положительно заряженной пластины конденсатора, φ1 – φ2 – разность потенциалов между его обкладками.}

_{Запишем формулы для электроемкости конденсаторов разного вида.}

1. _{Плоский конденсатор.}

_(8.5)

2. _{Цилиндрический конденсатор.}

_(8.6)

3. _{Сферический конденсатор.}

_(8.7)