6.4. Связь между потенциалом и напряженностью

_{Элементарная работа, совершенная при бесконечно малом перемещении заряда q в электрическом поле}

_{и dA = – dU = – d(qφ). Так как q = const, а , то}

_(6.9)

_{где El – проекция вектора на произвольное направление. В соответствии с формулой (6.9)}

_а

_(6.10)

_{Напряженность в какой-либо точке электростатического поля равна градиенту потенциала (см. Приложение) в этой точке, взятому с обратным знаком.}

_{Из выражений (6.2) и (6.4) можно получить интегральную формулу связи и φ, в которую входят две точки поля:}

_(6.11)

6.5. Графическое изображение электростатических полей

Для графического изображения электростатических полей используют линии вектора _{- они проводятся так, чтобы в каждой точке вектор был направлен по касательной к ним (рис. 6.2). Линии вектора нигде не пересекаются, они начинаются на положительных зарядах, заканчиваются на отрицательных или уходят в бесконечность. Примеры графического изображения полей точечных зарядов приведены на рис. 6.2б,в,г.}

_{В случае однородного поля (рис. 6.2∂) в каждой точке которого вектор одинаков и по модулю, и по направлению, линии представляют собой прямые, параллельные друг другу и отстоящие друг от друга на одинаковом расстоянии.}

_{Рис. 6.2}

_{Обычно линии проводят так, чтобы их густота в каждой точке поля определяла числовое значение вектора . Под густотой линий понимают количество линий, пронизывающих перпендикулярную к ним плоскую поверхность фиксированной площади.}

_{На рис. 6.2 пунктирными линиями изображены эквипотенциальные поверхности. Эквипотенциальная поверхность – это поверхность равного потенциала, в каждой точке поверхности потенциал φ будет одинаковым. Поэтому элементарная работа по перемещению заряда q по такой поверхности будет равна нулю: dA = – qdφ = 0. Соответственно вектор в каждой точке поверхности будет перпендикулярен к ней, то есть будет направлен по вектору нормали (рис. 6.2е).}

_{Условились проводить эквипотенциальные поверхности так, чтобы разность потенциалов между соседними поверхностями была одинаковой.}

Лекция 7

7.1. Поток и циркуляция вектора электростатического поля.

_{Теорема Гаусса для вектора}

_{Возьмем произвольный контур Г и произвольную поверхность S в неоднородном электростатическом поле (см. рис. 7.1а,б).}

Рис. 7.1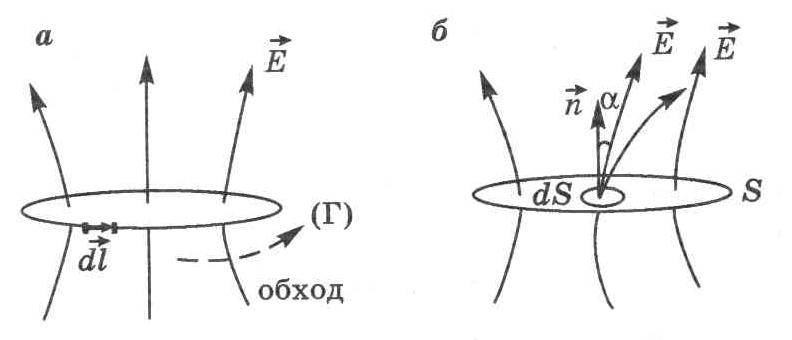

_{Тогда циркуляцией вектора по произвольному контуру Г называют интеграл вида}

_(7.1)

_{а потоком ФЕ вектора через произвольную поверхность S следующее выражение:}

_(7.2)

_{Входящие в эти формулы векторы и определяются следующим образом. По модулю они равны элементарной длине dl контура Г и площади dS элементарной поверхности S. Направление вектора совпадает с направлением обхода контура Г, а вектор направлен по вектору нормали к площадке dS (рис. 7.1).}

_{В случае электростатического поля циркуляция вектора по произвольному замкнутому контуру Г в соответствии с формулой (6.4) будет равна нулю:}

_(7.1а)

_{где Акруг – работа сил поля по перемещению точечного заряда q по этому контуру.}

_{Как отмечено в Прил., этот факт является признаком потенциальности электростатического поля. Следовательно, электрические заряды в электростатическом поле обладают потенциальной энергией.}

_{Уравнение (7.1а) в дифференциальной форме, справедливой для малой окрестности какой-либо точки электростатического поля, можно записать следующим образом (см. Прил. ):}

_(7.1б)

_{Теорема Гаусса в отсутствии диэлектрика (вакуум) формулируется следующим образом: поток вектора через произвольную замкнутую поверхность равен алгебраической сумме свободных зарядов , охватываемых этой поверхностью и деленной на ε0:}

_(7.2)

_{Покажем справедливость теоремы для случая поля точечного заряда. Пусть замкнутая поверхность представляет собой сферу радиусом R, в центре которой находится точечный положительный заряд q (рис. 7.2а).}

Рис. 7.2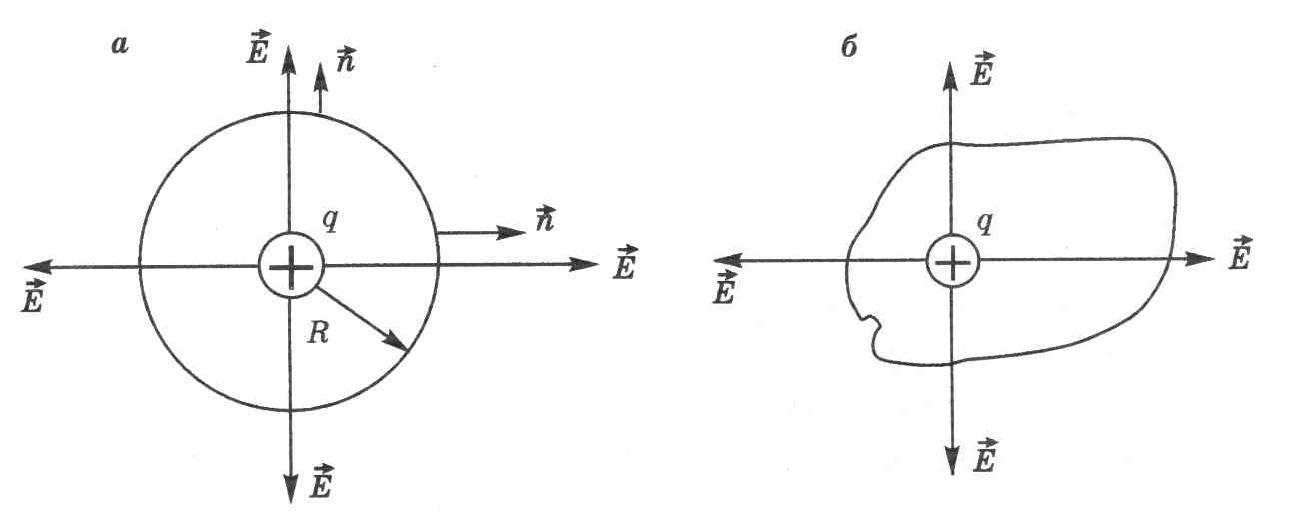

_Тогда

_(7.3)

_{Полученный результат не изменится, если вместо сферы выбрать произвольную замкнутую поверхность (рис. 7.2б), так как поток вектора численно равен количеству линий , пронизывающих поверхность, а число линий в случаях (а)} и (б) одинаково.

Подобные рассуждения с использованием принципа суперпозиции электростатических полей можно привести и в случае нескольких зарядов, попадающих внутрь замкнутой поверхности, что и подтверждает теорему Гаусса.

Запишем дифференциальную форму теоремы Гаусса, справедливую для любой малой окрестности какой-либо точки поля. С учетом формулы (П.10) Прил. получим

_(7.4)

_{где введена объемная плотность ρ свободных электрических зарядов}

_{то есть это заряд, содержащийся в единице объема.}