5.2. Релятивистские выражения массы и импульса тела

_{Уравнения Ньютона инвариантны по отношению к преобразованиям Галилея. Однако по отношению к преобразованиям Лоренца они оказываются не инвариантными, так как при больших скоростях движения масса тел зависит от скорости. Используя постулаты Эйнштейна и преобразования Лоренца, можно показать, что}

_{, (5.4)}

_г

Рис. 5.2

де _{m0 – масса покоящегося тела. Зависимость массы от скорости становится заметной только при очень больших скоростях, соизмеримых со скоростью света в вакууме (рис. 5.2). Поэтому в классической механике Ньютона, изучающей движения тел со сравнительно малыми скоростями (v << c), массы тел можно считать постоянными и равными их массам покоя.}

_{Следовательно, релятивистские выражения импульса и основного уравнения динамики поступательного движения имеют вид:}

_(5.5)

_(5.6)

5.3. Релятивистское выражение для энергии

_{Найдем выражение для кинетической энергии материальной точки в релятивистской механике. Приращение dT кинетической энергии материальной точки при элементарном перемещении равно работе ( , совершенной при этом перемещении силой , действующей на точку:}

_или

_{поскольку .}

_{Из основного уравнения релятивистской динамики (5.6) следует, что}

_.

_{Поэтому}

_.

_{Так как и , то}

_.

_{С другой стороны, как видно из формулы (5.4),}

_.

_{Таким образом, при изменении скорости материальной точки изменение ее кинетической энергии и массы пропорциональны друг другу:}

_(5.7)

_{Интегрирование полученного соотношения дает}

_{При v = 0, m = m0 и Т = 0. Отсюда для константы получается значение, равное – m0c}²_{. Следовательно, релятивистское выражение для кинетической энергии частицы имеет вид}

_(5.8)

_{В случае малых скоростей (v << c) формулу (5.8) можно преобразовать следующим образом:}

_{Мы пришли к ньютоновскому выражению для кинетической энергии частицы. Этого и следовало ожидать, поскольку при скоростях, много меньше скорости света, все формулы релятивистской механики должны переходить в соответствующие формулы ньютоновской механики.}

_{Перепишем формулу (5.8) в следующем виде:}

_{Анализируя это соотношение, Эйнштейн предположил, что полная энергия тела должна складываться из энергии его движения (кинетической) и энергии покоящегося тела (внутренней). Поэтому он отождествил второе слагаемое в этой формуле с внутренней энергией тела и назвал ее энергией покоя Е0, а сумму (Т + m0c}²_{) – полной энергией тела Е:}

_{Е0 = m0c}²_{; Е = mc}² _{. (5.9)}

_{Нужно отметить, что энергия покоя и полная энергия не включают в себя потенциальной энергии тела во внешних полях.}

_{Из выражений для импульса (5.5) и энергии (5.9) можно получить полезные формулы связи между ними:}

_;

_{В классической физике}

Лекция 6

6.1. Электрические заряды. Закон Кулона

В природе существует два рода электрических зарядов – положительные и отрицательные. На основании ряда опытов было выявлено, что электрический заряд любого тела состоит из целого числа элементарных зарядов, равных 1,6∙10^-19 Кл.

В замкнутой системе выполняется закон сохранения электрического заряда, который формулируется следующим образом: алгебраическая сумма электрических зарядов частиц замкнутой системы остается постоянной:

q₁ + q₂ + … =const.

Введение электрического заряда позволило сформулировать закон Кулона: силы, с которыми взаимодействуют два неподвижных точечных заряда в вакууме, прямо пропорциональны произведению их зарядов и обратно пропорциональны квадрату расстояния между ними; силы направлены вдоль прямой, соединяющей эти заряды (рис. 6.1а):

Рис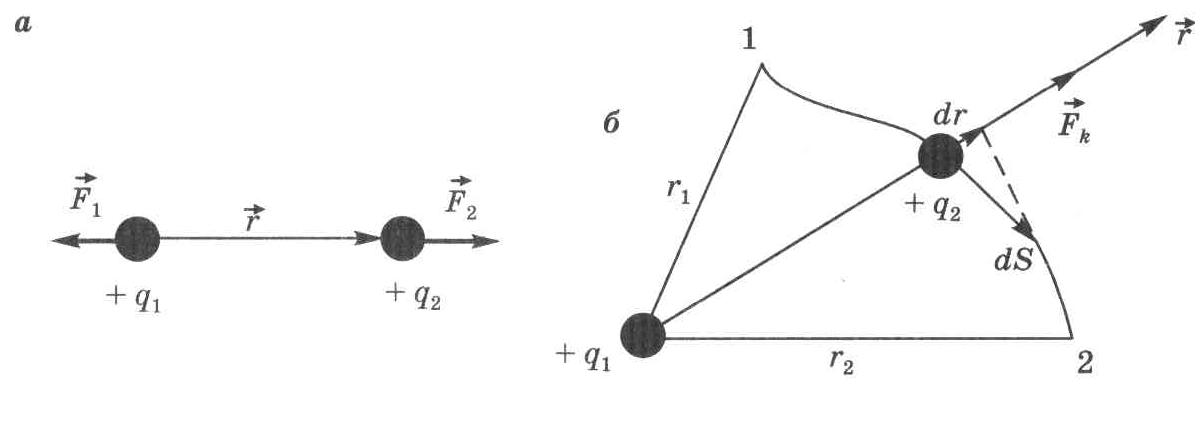. 6.1

_(6.1)

_{Входящая в формулу (6.1) величина ε0 = 8,85∙10}^-12 _{Ф/м называется электрической постоянной, она нужна при записи закона в международной системе единиц СИ.}