4.6. Специальная теория относительности. Постулаты Эйнштейна. Преобразования Лоренца

_{Созданная Эйнштейном в 1905 г. специальная теория относительности представляет собой физическую теорию пространства и времени. Основу этой теории образуют два постулата, которые носят названия принципа относительности Эйнштейна и принципа постоянства скорости света.}

_{Приведем несколько эквивалентных формулировок принципа относительности Эйнштейна:}

1. Никакими физическими опытами, находясь внутри исо, нельзя установить, движется она равномерно и прямолинейно или покоится;

2. Все законы физики выглядят, записываются одинаково во всех исо;

3. Все физические явления протекают одинаково во всех исо;

4. _{все законы физики инвариантны относительно преобразований Лоренца.}

_{Согласно второму постулату специальной теории относительности скорость света в вакууме одинакова во всех ИСО и не зависит от движения источника и приемника света.}

_{С помощью постулатов Эйнштейна можно показать, что координаты и время в разных системах отсчета связаны следующими соотношениями:}

_{Переход из К}^' _{в К: Переход из К в К}^'_:

_{y = y' y' = y}

_{z = z' z' = z}

_,

_{где β = v/c – относительная скорость. Записанные соотношения называют преобразованиями Лоренца. Преобразования Лоренца – это более общие, по отношению к преобразованиям Галилея, преобразования. Преобразования Лоренца справедливы для любых скоростей движения, а преобразования Галилея только для малых (v << c).}

Лекция 5

5.1. Следствия из преобразований Лоренца

Одновременность событий в разных системах отсчета. Пусть в системе К в точках с координатами х₁ и х₂ происходят одновременно два события в момент времени t₁ = t₂ = b. В соответствии с преобразованиями Лоренца в системе К' этим событиям будут соответствовать моменты времени

_.

_{Из данных формул видно, что в случае, если события в системе К пространственно разобщены (х1 ≠ х2), то в системе К' они не будут одновременными (t1}^' _{≠ t2}^'_{). Знак разности t2}^' _{– t1}^' _{определяется знаком выражения (β/c)(x1 – x2); следовательно, в разных системах К' (при разных β) разность t2}^' _{– t1}^' _{будет различна по величине и может отличаться по знаку. Это означает, что в одних системах событие 1 будет предшествовать событию 2, в других системах, наоборот, событие 2 будет предшествовать событию 1. Заметим, что сказанное относится лишь к событиям, между которыми отсутствует причинная связь.}

_{Продолжительность явления. Пусть в одной и той же точке с координатой х}^' _{= а системы К' происходит явление, которое начнется в момент времени t1}^' _{и закончится в момент времени t2'. Согласно преобразований Лоренца этим событиям соответствуют в системе К моменты времени}

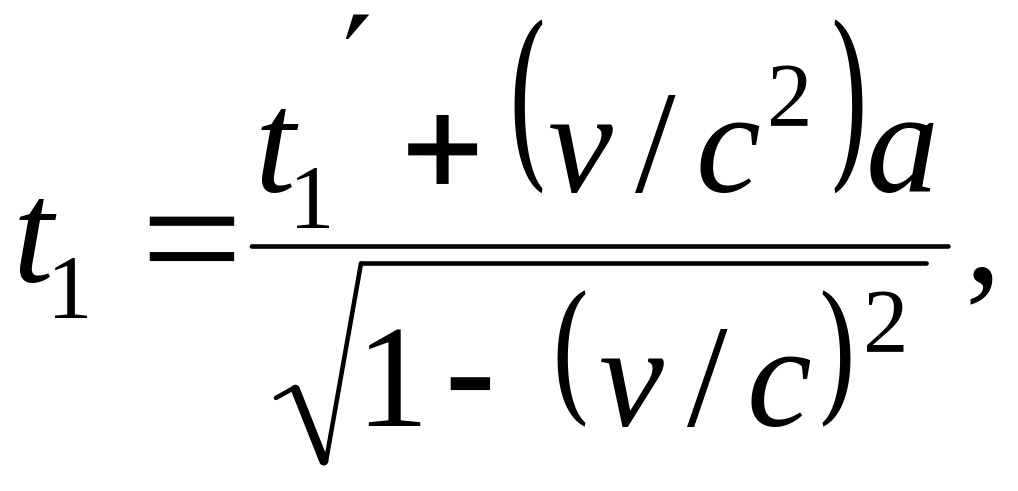
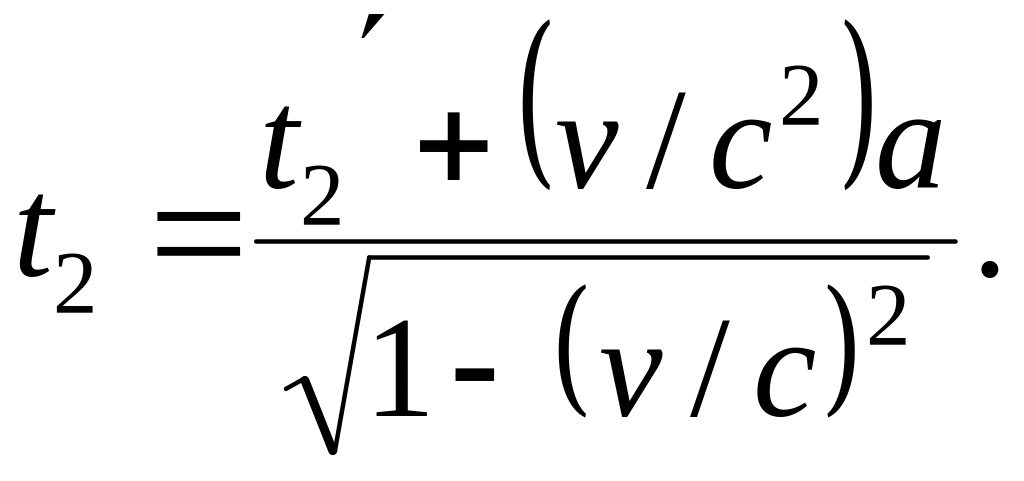_Отсюда

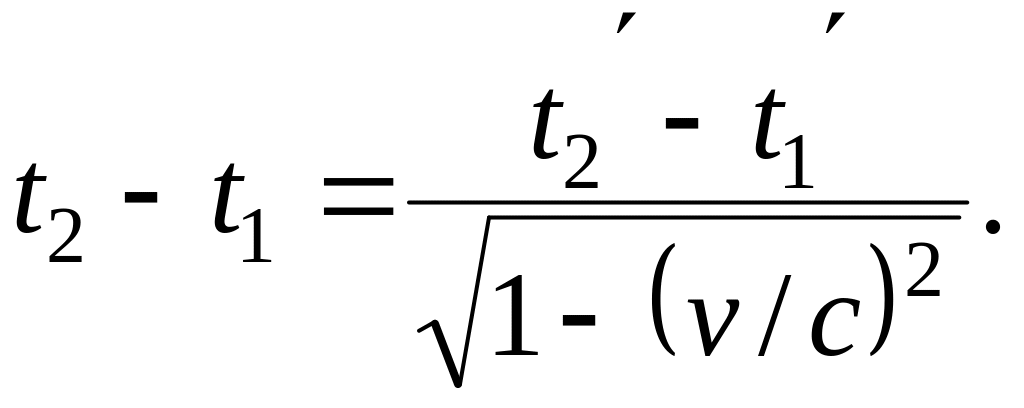
_{Введя обозначение t2 – t1 = ∆t и t2}^' _{– t1}^' _{= ∆t' , получим формулу}

_(5.1)

_{которая связывает промежутки времени между двумя событиями, измеренные в системах К и К}^'_{. Допустим, что оба события происходят с одной и той же частицей, которая покоится в системе К' и движется относительно системы К со скоростью v . Тогда ∆t' можно трактовать как промежуток времени, измеренный по часам, неподвижным относительно частицы, или, иными словами, измеренный по часам, движущимся вместе с частицей. Время, отсчитанное по часам, движущимся вместе с телом, называется собственное время этого тела и обозначается буквой τ. Таким образом, ∆t' = τ. С учетом этого формуле (5.1) можно придать вид}

_(5.2)

_{Длина тел в разных системах. Рассмотрим стержень, расположенный вдоль оси х' и покоящийся относительно системы отсчета К}^' _{(рис. 5.1). Длина его в этой системе l0 = x2'- x1}^'_{, где х1}^' _{и х2}^' _{– не изменяющиеся со временем t}^' _{координаты концов стержня. Относительно системы К стержень движется со скоростью v. Для определения его длины в этой системе нужно отметить координаты концов стержня} х₁ и х₂ в один и тот же момент времени t₁= t₂ = b. Их разность l = x₂ – x₁ дает длину стержня, измеренную в системе К. Чтобы найти соотношения между l₀ и l, следует взять ту из формул преобразований Лоренца, которая содержит х^', х и t.

Рис. 5.1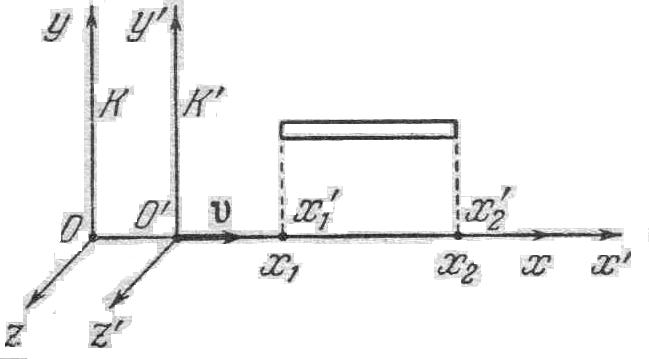

_откуда

_{или (5.3)}

_{Таким образом, длина стержня l, измеренная в системе отсчета, относительно которой он движется, оказывается меньше длины l0, измеренной в системе, относительно которой стержень покоится.}

_{Заметим, что в направлении осей y и z размеры стержня одинаковы во всех системах отсчета. Итак, у движущихся тел размеры их в направлении движения сокращаются тем больше, чем больше скорость движения. Это явление называют лоренцевым сокращением.}

_{Релятивистский закон сложения скоростей.}

_{Пусть вдоль совпадающих осей Ох и О}^'_х^' _{систем отсчета К и К}^' _{в их положительном направлении с постоянной скоростью движется тело. Проекция вектора скорости тела на координатные оси в СОК и К}^' _{соответственно равны:}

_СОК^'_{: u}^' _{= u}^'_{x = dx}^'_/dt^'_{, u}^'_{y = 0, u}^'_{z = 0;}

_{СОК: u = ux = dx/dt, uy = 0, uz = 0.}

_{Необходимо найти формулы связи между u и u}^'_{; в данном случае между ux и u}^'_{x. Для этого в преобразованиях Лоренца возьмем бесконечно малые приращения координат и времени:}

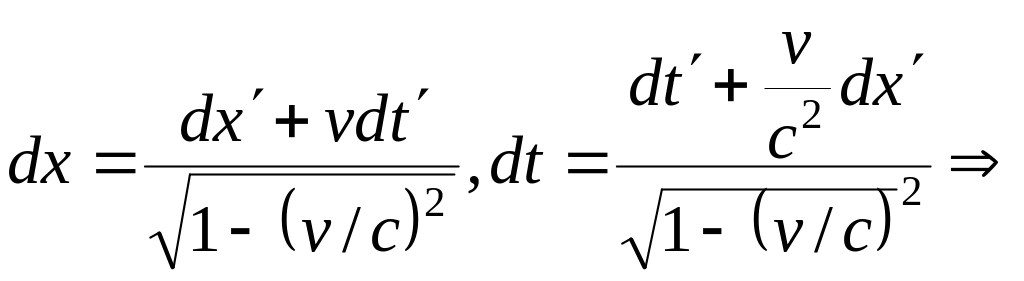
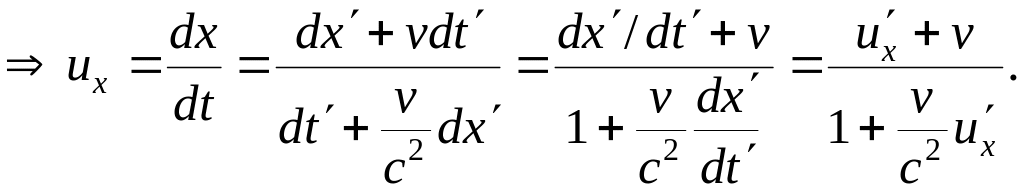
_Итак,

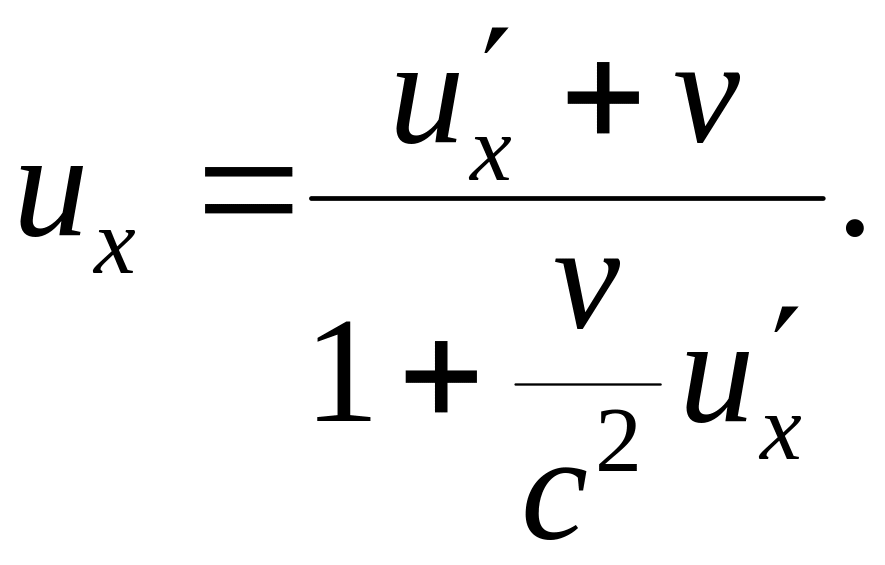_(5.4)

_{Аналогично можно получить обратную формулу связи}

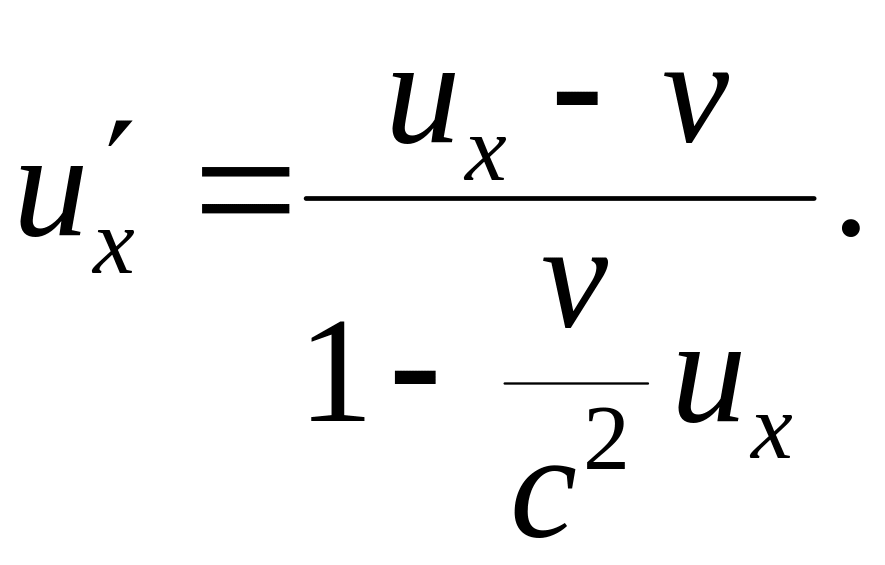_(5.5)

_{Формулы (5.4) и (5.5) представляют собой закон сложения скоростей в релятивистской механике. При малых скоростях движения тел (v << c) эти формулы переходят в закон сложения скоростей классической механики.}

_{Из закона сложения скоростей следует, что скорость движения тел не может быть больше скорости света в вакууме. Приведем в подтверждение этому факту пример.}

_{Пусть световой сигнал в СОК}^' _{распространяется вдоль оси О}^'_х^'_{, т. е. u}^' _{х = с. Тогда согласно формуле (5.4)}

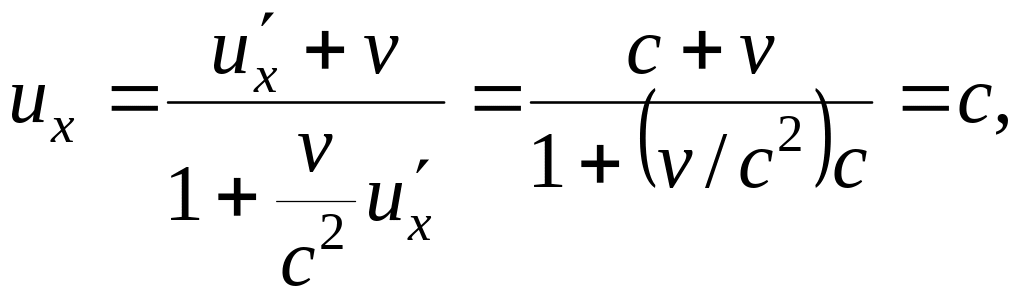
_{Что и должно было получиться.}