Создание планового съемочного обоснования на карьере.

Задание. Определить плановое положение точки Р, начала съемочного обоснования, геодезическими засечками.

Прямая геодезическая засечка.

Для решения прямой геодезической засечки графоаналитическим способом необходимо на план поверхности в масштабе 1:2000 по известным координатам Х_I, Y_I, Х_II, Y_II, Х_III, Y_III наносим пункты опорной сети.

Таблица 1. Координаты пунктов опорной сети:

Номера пунктов	Х, м	Y, м
I	29.2	59.5
II	229.6	118.9
III	239	299.4
IV	209.3	468.8

Для расчета координат точки Р₁ на исходных пунктах I, II, III измерим углы r₁ и r₂ в одном треугольнике и r₃ и r₄ во втором. Дополнительно, для повышения точности расчета, берём значения углов ₁, ₂.

Рассмотрим треугольник I-II-P₁.

Таблица 2. Исходные данные для вычисления координат пункта Р₁ из треугольника II-III-P₁.

Вершины	Углы, град	Х, м		У, м
II	r2=54o	229.6		118.9
I	r1=70o	29.2		59.5
P1	1=56o

Рассчитываем координаты пункта P₁ по следующим формулам:

, ,

где r – углы при пунктах опорной сети.

Для контроля рассчитаем координаты пункта I:

Рассмотрим треугольник II-III -P₁.

Таблица 3. Исходные данные для вычисления координат пункта Р₁ из треугольника II-III -P₁.

Вершины	Углы, град	Х, м		У, м
III	r4=77o	239		299.4
II	r3=55o	229.6		118.9
P1	2=48o

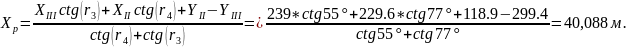
Из решения двух треугольников разница в координатах точки Р₁ составляет

, которая не превышает 0,6 мм на плане в масштабе съёмки (1,2м).

Среднее значение координат точки Р₁ из двух треугольников:

X_P1=39,98, Y_P1=260,361

Рассчитаем среднеквадратическую погрешность М_Р.

Для треугольника I-II-P₁

0,027

Для треугольника II-III -P₁.

Где =15 - средняя квадратическая ошибка измерения углов;

=206265 ;

В₁=209, В₂=180,7 – базисы прямой засечки (расстояние между пунктами опорной сети) определяется решением обратной геодезической засечки.

В результате средняя квадратическая погрешность положения пункта P₁ относительно пунктов опорной сети из двух треугольников составила 0,032м и не превышает допустимой величины (0,8м).