7. Общие сведения о магнитных цепях аппаратов и магнитных материалах: величины, характеризующие магнитные цепи, аналогия с электрическими цепями.

Магнитной цепью называется совокупность деталей, через которые замыкается магн. поток. Она состоит из магнитопровода, источника МДС и возд. зазора. В замкн. системах зазор отсутствует. Магн. цепь хар – ся след. параметрами: магн. потоком Ф[Вб] , магн. индукцией В=Ф/S[Вб/м²], напряженностью магн. поля Н [А/м], магн. проницаемостью µ=В/Н [Вб/А·м] µ₀ = 4*π*10^-7[В/(А·м)], МДС F= i·w [A], магн. проводимостью G [Вб/А].

Магнитная цепь Электрическая цепь

Магнитный поток Ф, Вб Ток I, А

Намагничивающая сила Iω, А Напряжение U, В

Напр. магн. поля Н, А/м Плотность тока j, А/м2

Индукция В, Т=Вб/м2 Напр. эл. поля Е, В/м

Магн. прониц. µ, Г/м Уд. проводимость σ, 1/(Ом·м)

Уд. магн. сопротивление ρм , м/Г Уд. эл. сопротивление ρэ , Ом·м

Магн. сопр. Rм , 1/Г Эл. сопр. Rэ , Ом

Магн. проводимость Gм , Г Эл. проводимость Gэ , 1/Ом

В качестве материалов исп – ся магнитомягкие материалы, обладающие узкой петлей гистерезиса и высокой магн. проницаемостью, и магнитотвердые, обладающие широкой петлей гистерезиса и малой проницаемостью. Все они делятся на ферросплавы и ферриты. Ферросплавы – мат – лы, в кот. входят в основном Fe. Ферриты – прессованные материалы из смеси окислов железа с окислами никеля, цинка, свинца и др. К ферросплавам относят электротехнические стали (сплавы железа в основном с кремнием) и пермаллои (сплав железа с никелем). Электротехн. стали и железо имеют высокие индукции насыщения, поэтому широко применяются в электромагнитах, т.к. это позволяет создать большие тяговые усилия. Для ферритов характерно очень высокое эл. сопротивление, поэтому их применяют при очень высоких частотах полей без существенных потерь на вихревые токи. Индукция насыщения и магн. прониц. ферритов невысокие.

8. Тяговые силы в электромагнитах: расчет для электромагнита постоянного тока, статическая тяговая характеристика.

Расчет силы тяги электромагнита постоянного тока.

Средняя сила тяги на ходе якоря от δ1 до δ₂

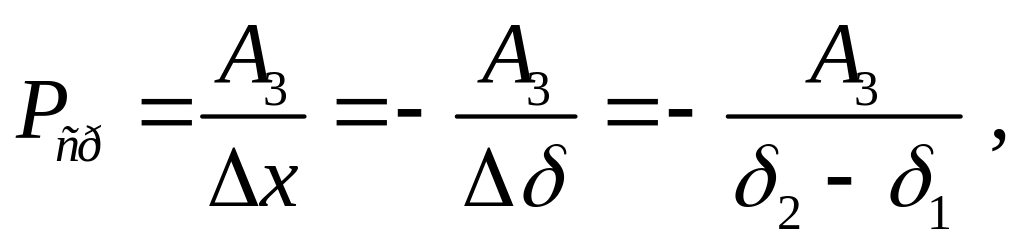
Где ∆х: — перемещение якоря, а ∆ δ — изменение зазора.

Таким образом, тяговая сила, развиваемая на ходе яко­ря ∆х равна работе, совершенной электромагнитом, делен­ной на это перемещение ∆х. Если перейти на бесконечно малое изменение зазора dx и учесть, что

Зависимость Ψ(i) при неизменном I_y в обмотке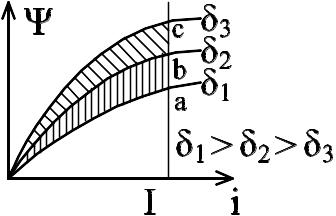

x= δ_1-б и dx = -d δ, получим .

Сила тяги Р действует в сторону уменьшения зазора. Очевидно, что для каждого элементарного перемещения якоря можно определить свое значение А₃ и найти среднюю силу тяги, развиваемую на данном участке хода якоря. Если при перемещении якоря ток в обмотке можно счи­тать неизменным и равным I, то функции W(i) для различных за­зоров представляются кривыми на рисунке.

Зависимость тяговой силы электромагнита от рабочего зазо­ра при неизменном токе в обмот­ке называется статической тяговой характеристи­кой электромагнита. Ес­ли в электромагните вместо ли­нейного перемещения якоря пре­дусмотрен его поворот, то под ста­тической тяговой характеристи­кой понимается зависимость мо­мента М на якоре от угла его поворота а, снятая при не­изменном токе в обмотке.

Для зазора δ_1cp= (δ1+ δ2)/2 силу тяги можно найти как

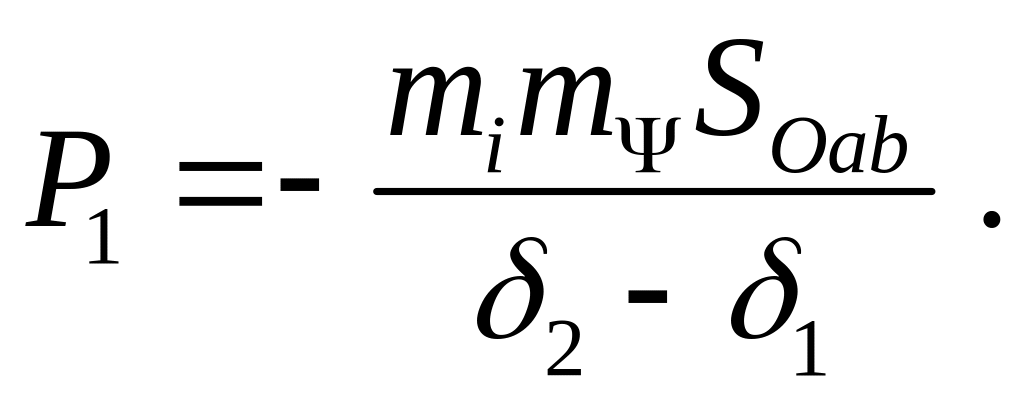
Для зазора δ_2cp= (δ2+ δ3)/2

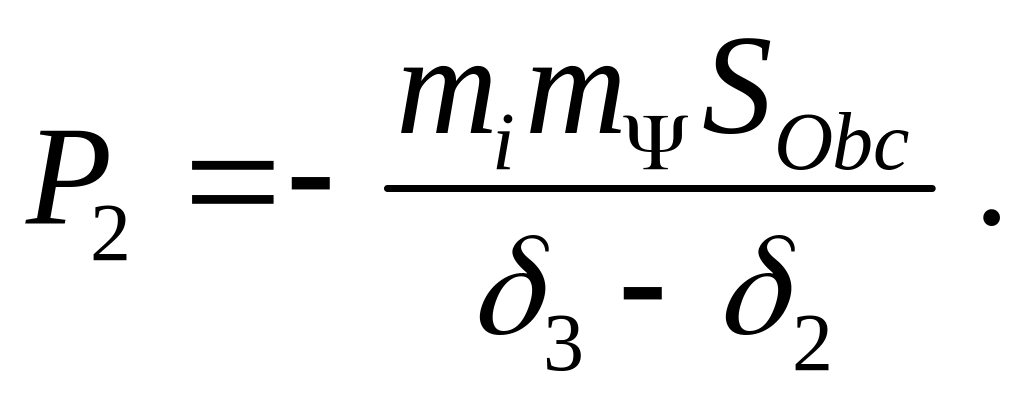
Для снятия статической характеристики в рабочий за­зор электромагнита ставится немагнитная прокладка, пос­ле чего к электромагниту подводится напряжение. С помо­щью динамометра постепенно увеличивается противодей­ствующая сила до тех пор, пока якорь не оторвется от сердечника. Эта сила в момент отрыва будет равна стати­ческой силе тяги при зазоре, равном толщине прокладки. После этого меняют толщину прокладки и опыт повторяют при новом значении рабочего зазора.

Сила тяги, развиваемая электромагнитом, может быть рассчитана с помощью формулы Максвелла, полученной из анализа магнитного поля, действующего на поверхности по­люсов. Если поле в рабочем зазоре равномерно и по­люсы ненасыщены, то для электромагнита с одним рабочим зазором формула Максвелла имеет вид:

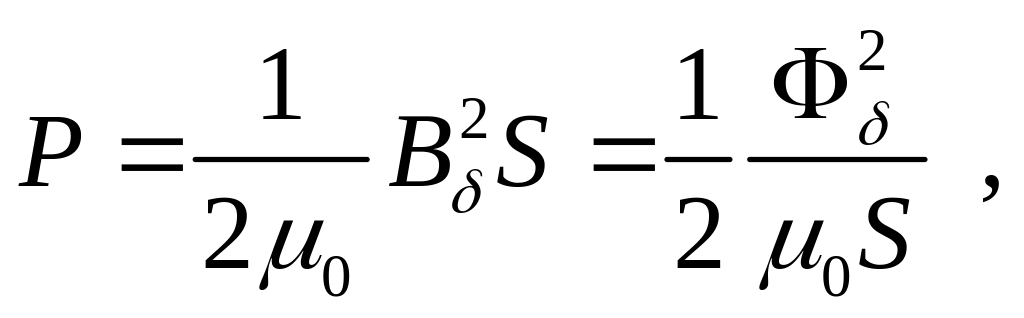
где В_δ и Ф_δ — индукция, Тл, и магнитный поток, Вб, в ра­бочем зазоре; S — площадь полюса, м².

Если клапанный электромагнит имеет два рабочих за­зора при том же значении Ф_δ магнитного по­тока в зазоре, то сила тяги удваивается: