Примерный ответ на билет №5
Прямоугольные проекции. Использование их в практической деятельности
Если проецирующие лучи , с помощью которых строится проекция предмета, параллельны друг другу , проецирование называется параллельным. В том случае , когда проецирующие лучи перпендикулярны плоскости проекции, т.е. составляют с ней угол 90 градусов, проецирование называется прямоугольным . Полученная при этом проекции называется прямоугольной.
Прямоугольное проецирование широко используется для построения изображений на чертежах.
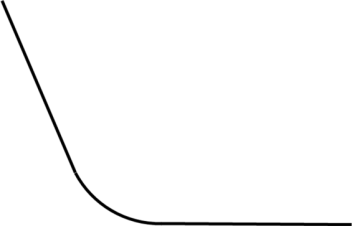
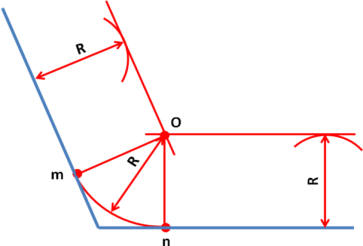
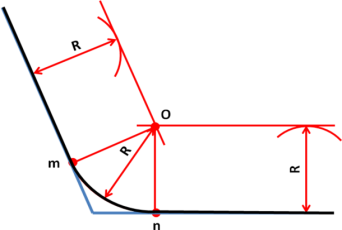
2.Сопряжение тупого, прямого и острого угла
Для построения сопряжения надо найти центр сопряжения и точки сопряжения, знать радиус сопряжения .
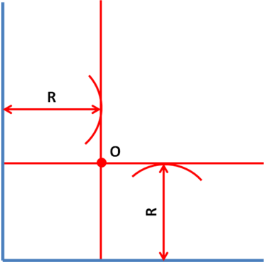
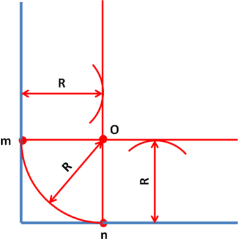
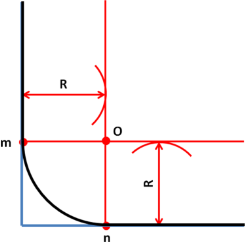
- Аналогично строим сопряжение двух прямых, составляющих острый угол. (Учащиеся, которые поняли алгоритм построения, могут самостоятельно выполнить чертеж.)
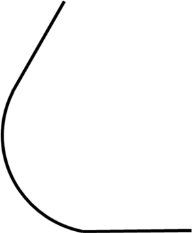
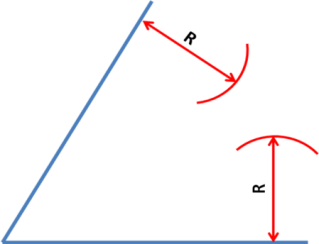
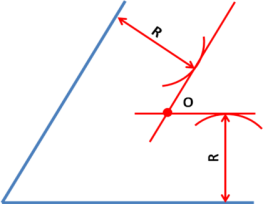
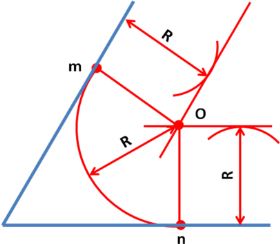
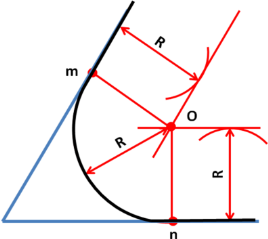
- Сопряжение двух прямых, составляющих тупой угол, выполнить самостоятельно.
Примерный ответ на билет №7
Разрезы: назначение , получение, классификация
У деталей , имеющих внутренние пустоты( отверстия, вырезы и др.) , надо по возможности четче показать на чертеже их контуры. Поэтому в этом случае применяют разрез.
Разрез- это изображение предмета, мысленно рассеченного плоскостью( или несколькими плоскостями ). На разрезе показывают то, что находиться в секущей плоскости и за ней.
Если секущая плоскость совпадает с плоскостью симметрии детали и разрез расположен в проекционной связи, его не обозначают. В остальных случаях обозначают так же, как сечения разомкнутой линией. Стрелки с буквами показывают направление взгляда. Над разрезом пишут те же буквы через тире.
Разрез на чертеже выделяют штриховкой, которую наносят тонкими линиями под углом 45граусов.
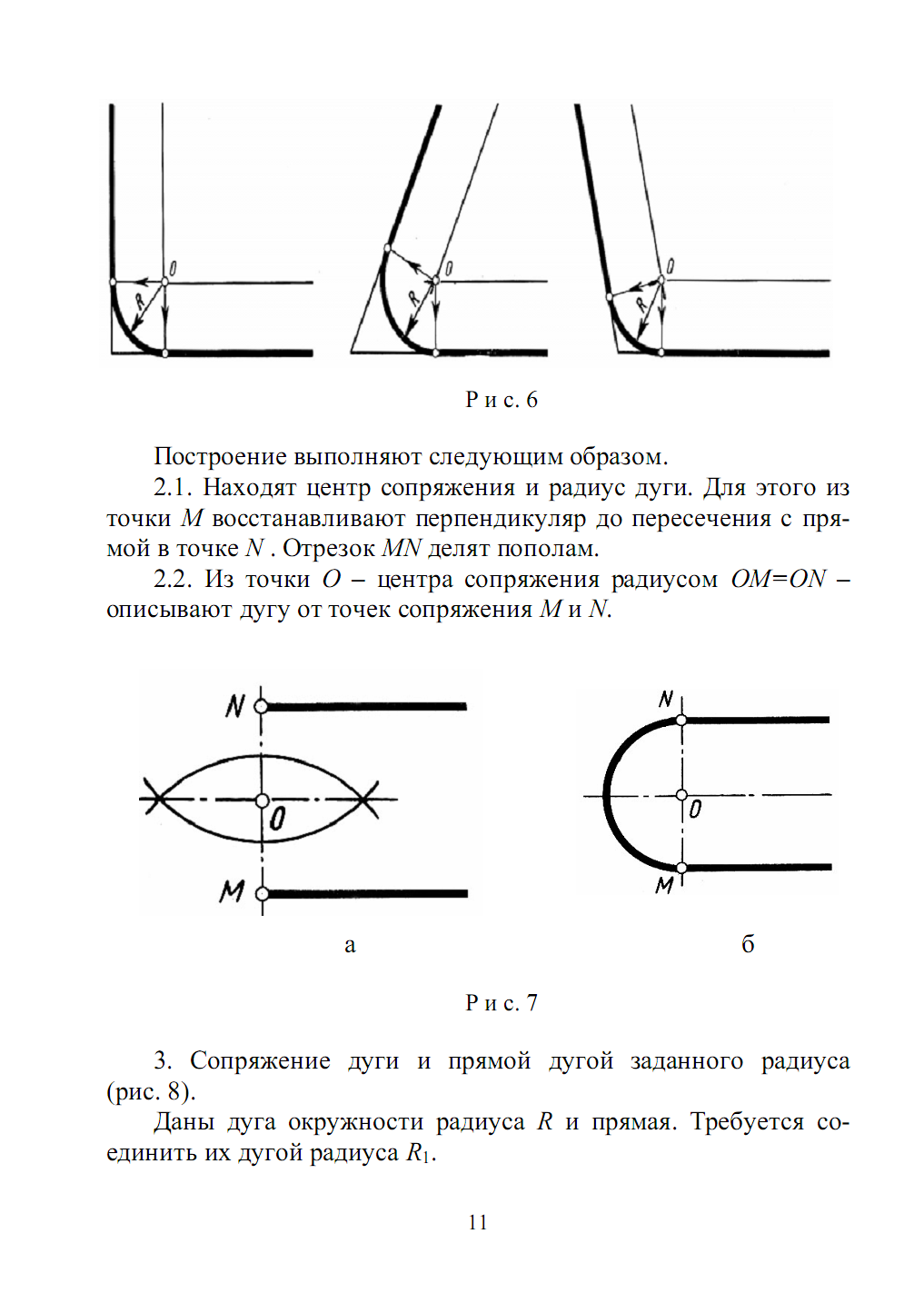
Сопряжение двух параллельных прямых
- Находят центр сопряжения и радиус дуги . Для зтого из точки М восстанавливают перпендикуляр до пересечения с прямой в точке N. Отрезок МN делят пополам.
- Из точки О- центра сопряжения радиусом ОМ=ОN- описывают дугу от точек сопряжения М и N.
Примерный ответ на билет №8
Простые разрезы
Разрез , полученный рассечением детали одной плоскостью, называется простым. В зависимости от положения секущей плоскости простые разрезы делятся на фронтальные, горизонтальные, профильные.
На одном чертеже может быть несколько разрезов. Но каждый из них должен быть целесообразным.
Разрезы обычно располагаются в проекционной связи : фронтальный – на месте главного вида, профильный на месте – вида слева, горизонтальный – на виде вида сверху.
«Сопряжение двух окружностей дугой заданного радиуса»(внутреннее)
Даны две окружности, наша задача построить внутреннее сопряжение заданным радиусом.
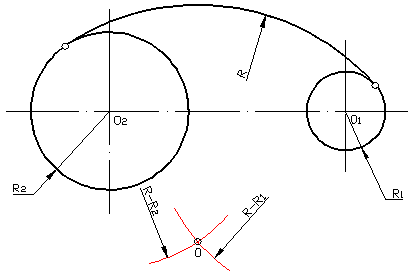
Находим центр сопряжения, для этого ставим ножку циркуля в центры окружностей и проводим дугу радиусом равным радиус сопряжения - радиус окружности. Получили точку пересечения – это и есть центр сопряжения точка Ос.
Находим точки сопряжения, для этого соединяем центр сопряжения с центрами окружностей и на дугах окружностей получаем точки пересечения – это и есть точки сопряжения.
3. Проводим дугу из центра сопряжения, радиусом равным радиусу сопряжения, соединяя точки сопряжения.Получили:
внутреннее сопряжение двух окружностей дугой заданного радиуса.