1.2. Соединение в треугольник
Если три фазы приемника
с фазными сопротивлениями
,
,
,
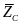включить
непосредственно между линейными
проводами трехпроводной цепи, то получим
соединение приемников треугольником
(рис. 3).
Так как при соединении треугольником к концам каждой фазы потребителя приложено линейное напряжение, то линейные напряжения будут являться одновременно и фазными, т. е.
(1)
Рис. 3. Схема соединение потребителей треугольником
Если пренебречь сопротивлениями линейных проводов, то фазные напряжения приемника равны соответствующим линейным напряжениям источника питания, а они практически неизменны.
.
Фазные и линейные токи не равны между собой, соотношение между ними можно получить по первому закону Кирхгофа, записанному для узлов схемы геометрической форме
.
Из уравнений (2) следует, что любой из линейных токов равен геометрической разности токов тех двух фаз нагрузки, которые соединяются с данным линейным проводом.
Независимо от характера нагрузки геометрическая сумма линейных токов в трехпроводной цепи равна нулю:
.
Если сопротивления фаз приемника известны, то пренебрегая сопротивлением линейных проводов, величину фазных токов определяют по закону Ома
При симметричной нагрузке линейные и фазные токи равны по величине, причем
.
Активная и реактивная мощности определятся с учетом выражения(1) для симметричной цепи таким образом:
В случае, когда сопротивлениями в линейных проводах нельзя пренебрегать, расчет такой цепи может быть выполнен по любому известному методу, например, методу контурных токов.
Пример 2. Расчет трехфазной цепи соединенной в треугольник методом контурных токов. Расчетная схема приведена на рис. 4.
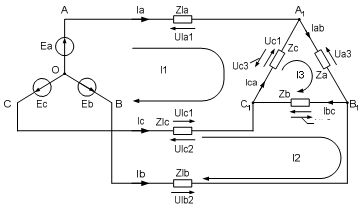
Рис. 4. Расчетная схема трехфазной цепи при соединении нагрузки в треугольник для метода контурных токов
% Программа расчета цепи трехфазного тока звезда/треугольник
% методом контурных токов
% Исходные данные
clc
E=220;
Zla=5+5*j;
Zlb=6-3*j;
Zlc=7+5*j;
Za=50+50*j;
Zb=75+20*j;
Zc=45+10*j;
% РЕШЕНИЕ
% Определяем фазные и линейные напряжения генератора
Ea=E;
Eb=E*(-0.5-0.866*j);
Ec=E*(-0.5+0.866*j);
Eab=Ea-Eb;
Ebc=Eb-Ec;
Eca=Ec-Ea;
% Вводим матрицы коэффициентов уравнений по законам Кирхгофа
A=[(Zla+Zlc+Zc) -Zlc -Zc;
-Zlc (Zlb+Zb+Zlc) -Zb;
ZcZb-(Zc+Za+Zb)];
B=[(Ea-Ec) 0 0;
(Ec-Eb) 0 0;
0 0 0];
I=(A\B);
disp('Контурные токи выводятся в следующем порядке: I1,
I2, I3, А')
k=1:1:3;
I=I(k,1)
disp('Реальные токи будут равны, А:')
Ia=I(1,1)
Ib=-I(2,1)
Ic=I(2,1)-I(1,1)
Iab=I(3,1)
Ibc=I(3,1)-I(2,1)
Ica=I(3,1)-I(1,1)
% Определяем фазные напряжения и потери в линии
disp('Фазные напряжения:Ua, Ub, Uc, В')
Ua=Za*Iab
Ub=Zb*Ibc
Uc=Zc*Ica
disp('Действующие значения фазных напряжений:Ua, Ub,Uc, В')
Uda=abs(Ua)
Udb=abs(Ub)
Udc=abs(Uc)
disp('ПотеривлинииUIa, UIb, UIc, В')
Ula=Zla*Ia
Ulb=Zlb*Ib
Ulc=Zlc*Ic
%Мощность генератора Sg:
Sg=Ia'*Ea+Ib'*Eb+Ic'*Ec;
%МощностьнагрузкиSn:
Sn=abs(Iab)^2*Za+abs(Ibc)^2*Zb+abs(Ica)^2*Zc+abs(Ia)^2*Zl
a+abs(Ib)^2*Zlb+abs(Ic)^2*Zlc;
Sb=Sg-Sn;
disp([' Мощностьгенератора, ВАSg =',num2str(Sg)])
disp([' Мощностьнагрузки, ВАSn =',num2str(Sn)])
disp([' Балансмощности, ВАSb =',num2str(Sb)])
clearall
В результате выполнения программы имеем:
Контурные токи выводятся в следующем порядке: I1, I2, I3, А
I =
7.6485 - 4.8642i
5.2643 + 3.5032i
3.9671 - 0.53968i
Реальные токи будут равны, А:
Ia =7.6485 - 4.8642i
Ib =-5.2643 - 3.5032i
Ic =-2.3842 + 8.3675i
Iab =3.9671 - 0.53968i
Ibc =-1.2972 - 4.0429i
Ica =-3.6814 + 4.3245i
Фазные напряжения: Ua, Ub, Uc, В.
Ua =
225.34 + 171.37i
Ub =
-16.431 - 329.16i
Uc =
-208.91 + 157.79i
Действующие значения фазных напряжений: Ua, Ub, Uc, В.
Uda =
283.1
Udb =
329.57
Udc =
261.8
Потери в линии UIa, UIb, UIc, В.
Ula =
62.564 + 13.922i
Ulb =
-42.096 - 5.2264i
Ulc =
-58.527 + 46.651i
Мощность генератора, ВА Sg =4785.6232+2153.9125i
Мощность нагрузки, ВА Sn =4785.6232+2153.9125i
Баланс мощности, ВА Sb =0-4.5475e-013i
Как видим, и в примере 1 и в примере 2 баланс мощности сошелся, значит, расчет выполнен, верно.
Приложение 2