Приклад виконання завдання
Розглянемо
приклад виконання завдання для заданих
спостережень обсягів перевезень
пасажирів на маршруті по днях місяця:
54, 53, 53, 55, 59, 52, 57, 59, 59, 64, 56, 52, 64, 52, 58, 61, 62, 64, 54, 62, 51, 61, 58, 61, 61.
Розв’язок.
1.
Розрахунок
значень
,
,
,
виконуємо в таблиці 1.3.
Таблиця 1.3 – Розрахунок значень , , ,
t |
|
|
|
|
|
1 |
54 |
– |
– |
– |
– |
2 |
53 |
0 |
1 |
1 |
–1 |
3 |
53 |
0 |
0 |
0 |
0 |
4 |
55 |
1 |
0 |
1 |
1 |
5 |
59 |
1 |
0 |
1 |
1 |
6 |
52 |
0 |
1 |
1 |
–1 |
7 |
57 |
0 |
0 |
0 |
0 |
8 |
59 |
0 |
0 |
0 |
0 |
9 |
59 |
0 |
0 |
0 |
0 |
10 |
64 |
1 |
0 |
1 |
1 |
11 |
56 |
0 |
0 |
0 |
0 |
12 |
52 |
0 |
0 |
0 |
0 |
13 |
64 |
0 |
0 |
0 |
0 |
14 |
52 |
0 |
0 |
0 |
0 |
15 |
58 |
0 |
0 |
0 |
0 |
16 |
61 |
0 |
0 |
0 |
0 |
17 |
62 |
0 |
0 |
0 |
0 |
18 |
64 |
0 |
0 |
0 |
0 |
19 |
54 |
0 |
0 |
0 |
0 |
20 |
62 |
0 |
0 |
0 |
0 |
21 |
51 |
0 |
1 |
1 |
–1 |
22 |
61 |
0 |
0 |
0 |
0 |
23 |
58 |
0 |
0 |
0 |
0 |
24 |
61 |
0 |
0 |
0 |
0 |
25 |
61 |
0 |
0 |
0 |
0 |
|
|
|
|
r = 6 |
d = 0 |
2.
За
табл. 1.1
для
n = 25
знаходимо: μ = 5,593;
= 1,78;
= 2,363.
3. Використовуючи формули (1.2), обчислюємо значення критерію Стьюдента для випадкових величин r і d:
; 
.
4. За таблицею квантилей розподілу Стьюдента (додаток А) для рівня значимості α = 0,05 і кількості ступенів вільності f = 25 – 3 = 22 знаходимо критичне значення =2,07.
5.
Так як
і
,
то попит на перевезення пасажирів на
приміському маршруті вважаємо
стаціонарним
і в середньому і в дисперсії.
Графік попиту на перевезення наведений
на рисунку 1.1.
yt
t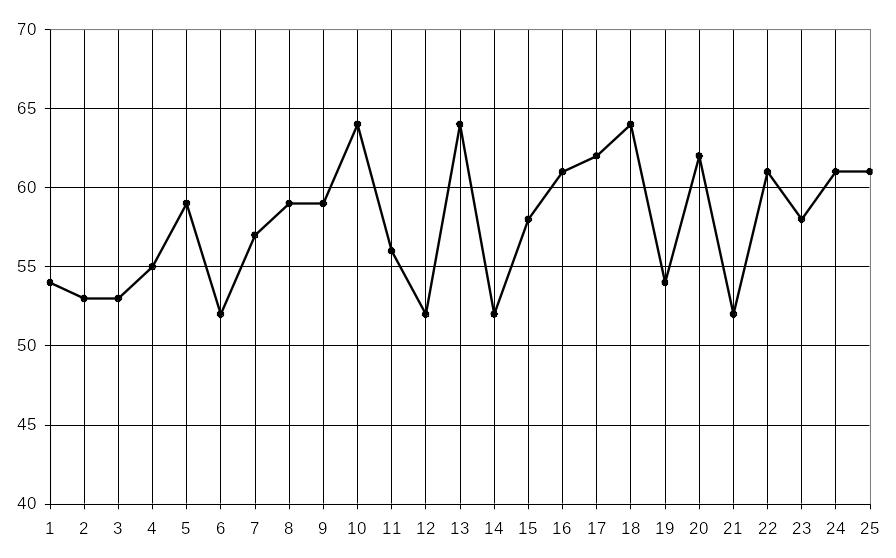
Рисунок 1.1 – Динаміка попиту на пасажирські перевезення
на приміському маршруті