Контрольні запитання
1. Дайте визначення наступним визначенням: прогноз, динамічний ряд, рівень динамічного ряду, період упередження.
2. Які види прогнозів розрізняють за тривалістю періоду упередження ?
3. У чому полягає сутність методу ковзної середньої?
4. Викладіть порядок розрахунків прогнозу методом експоненціального згладжування за лінійною та квадратичною моделями. З яких міркувань обирають константу згладжування ?
5. Яким чином оцінюють похибку та якість вироблених прогнозів ?
Практичне заняття №2 моделювання сезонних коливань обсягів вантажопереробки
Мета заняття: закріплення знань і придбання навичок використання математико-статистичних методів дослідження і аналізу величини фактичного обсягу вантажопереробки в окремі періоди часу планового періоду.
Стисла теоретична довідка
При періодичних (сезонних) коливаннях обсягів перевезень і вантажообігу шукану функцію, що виражає змінювання досліджуваних показників у часі, подають нескінченим рядом синусоїдних і косинусоїдних функцій з певним періодом (рядом Фур’є).
Кожен член суми є гармонікою, причому період першої гармоніки дорівнює довжині заданого основного періоду, другої – половині основного періоду, третьої – третині основного періоду і т.д.
У
загальному випадку, якщо є п
спостережень, то кількість гармонік
k
не перевищує
.
Відповідні їм значення функції
записуються сумою
,
(2.1)
де п – повний період (загальна кількість спостережень);
k – номер гармоніки.
Використовуючи метод найменших квадратів, параметри ряду Фур’є визначають за формулами.
;
(2.2)
;
(2.3)
.
(2.4)
Для
зручності розрахунків основний період
доцільно поділити на 12 частин. Тоді для
окремих часових періодів величина
змінної
в формулах (2.3) і (2.4) приймає значення,
наведені в таблиці 2.1.
Таблиця 2.1 – Величина змінної
t |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
z |
|
|
|
|
|
|
|
|
|
|
|
|
Приймаючи кількість гармонік k = 1, 2, 3, … визначають всі значення sin(kz) і cos(kz) (таблиця 2.2).
Таблиця 2.2 – Значення sin(kz) і cos(kz) для т = 6 гармонік
t |
sin(kz) |
cos(kz) |
||||||||||
k |
k |
|||||||||||
1 |
2 |
3 |
4 |
5 |
6 |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
0,500 |
0,866 |
1 |
0,866 |
0,500 |
0 |
0,866 |
0,500 |
0 |
-0,500 |
-0,866 |
-1 |
2 |
0,866 |
0,866 |
0 |
-0,866 |
-0,866 |
0 |
0,500 |
-0,500 |
-1 |
-0,500 |
0,500 |
1 |
3 |
1,000 |
0,000 |
-1 |
0,000 |
1,000 |
0 |
0,000 |
-1,000 |
0 |
1,000 |
0,000 |
-1 |
4 |
0,866 |
-0,866 |
0 |
0,866 |
-0,866 |
0 |
-0,500 |
-0,500 |
1 |
-0,500 |
-0,500 |
1 |
5 |
0,500 |
-0,866 |
1 |
-0,866 |
0,500 |
0 |
-0,866 |
0,500 |
0 |
-0,500 |
0,866 |
-1 |
6 |
1,000 |
0,000 |
0 |
0,000 |
0,000 |
0 |
-1,000 |
1,000 |
-1 |
1,000 |
-1,000 |
1 |
7 |
-0,500 |
0,866 |
-1 |
0,866 |
-0,500 |
0 |
-0,866 |
0,500 |
0 |
-0,500 |
0,866 |
-1 |
8 |
-0,866 |
0,866 |
0 |
-0,866 |
0,866 |
0 |
-0,500 |
-0,500 |
1 |
-0,500 |
-0,500 |
1 |
9 |
-1,000 |
0,000 |
1 |
0,000 |
-1,000 |
0 |
0,000 |
-1,000 |
0 |
1,000 |
0,000 |
-1 |
10 |
-0,866 |
-0,866 |
0 |
0,866 |
0,866 |
0 |
0,500 |
-0,500 |
-1 |
-0,500 |
0,500 |
1 |
11 |
-0,500 |
-0,866 |
-1 |
-0,866 |
-0,500 |
0 |
0,866 |
0,500 |
0 |
-0,500 |
-0,866 |
-1 |
12 |
0,000 |
0,000 |
0 |
0,000 |
0,000 |
0 |
1,000 |
1,000 |
1 |
1,000 |
1,000 |
1 |
Наприклад, перша гармоніка ряду Фур’є
,
де
;
;
.
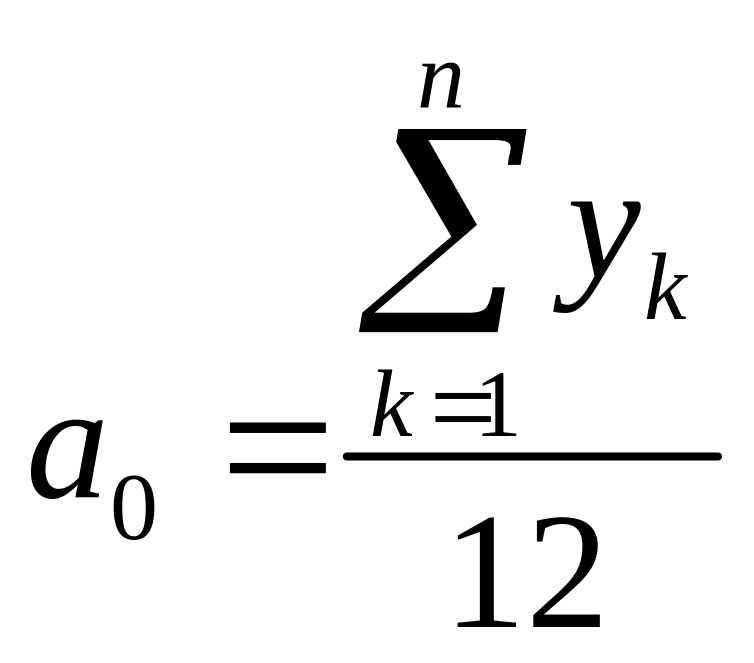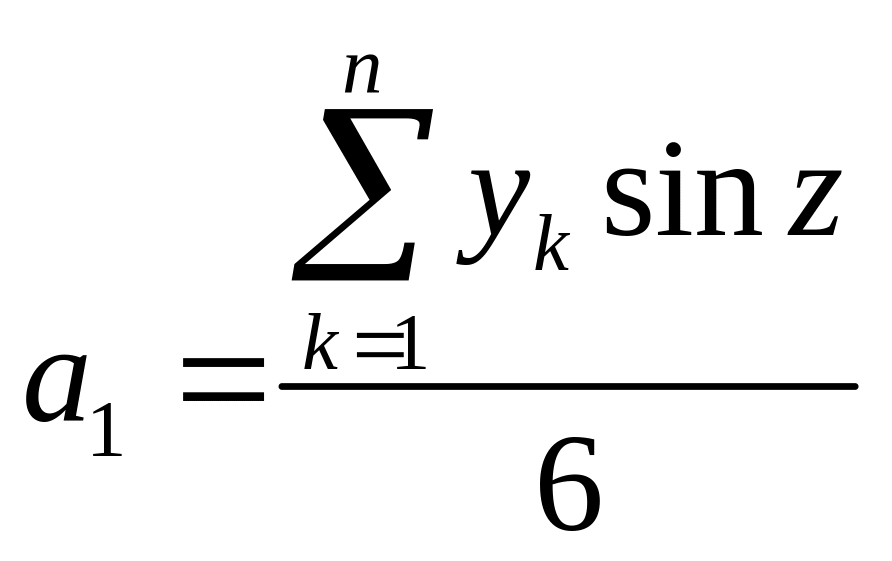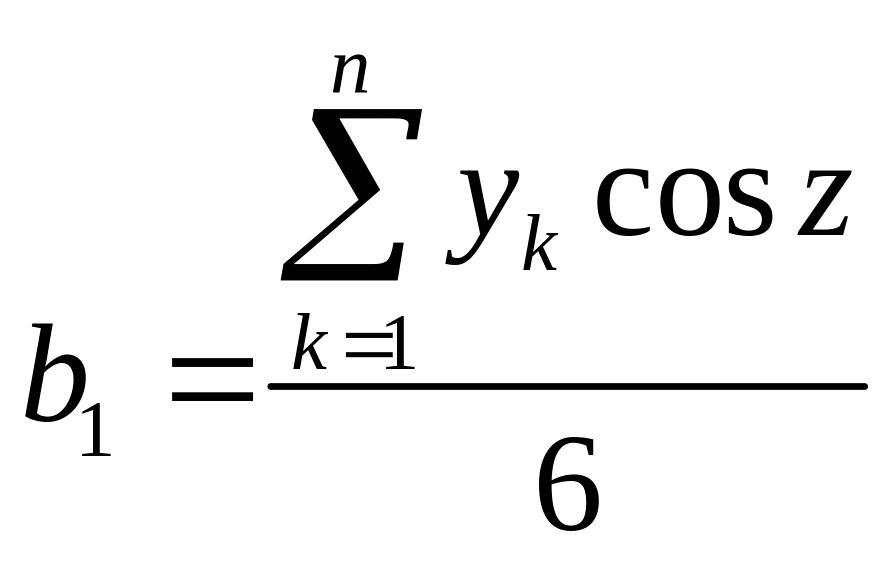Ряд Фур’є з двома гармоніками має вигляд
.
Тут
;
.
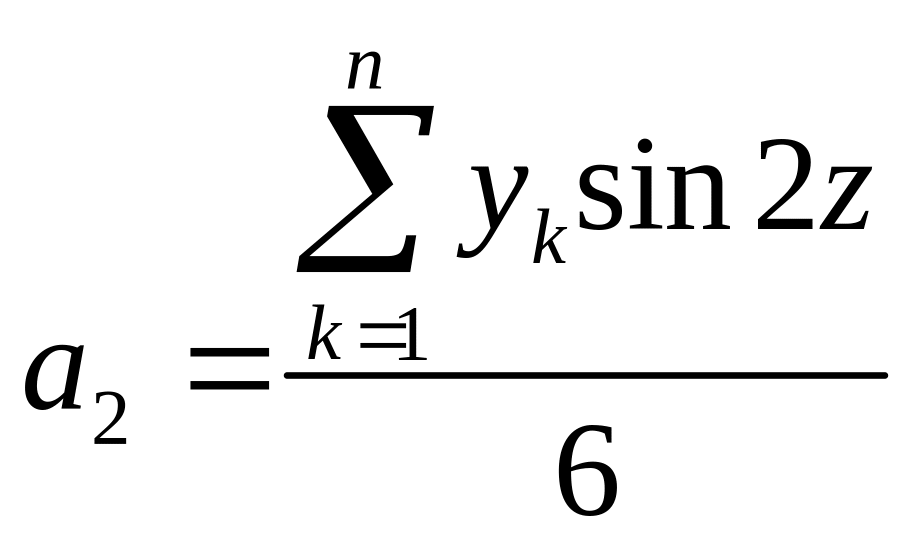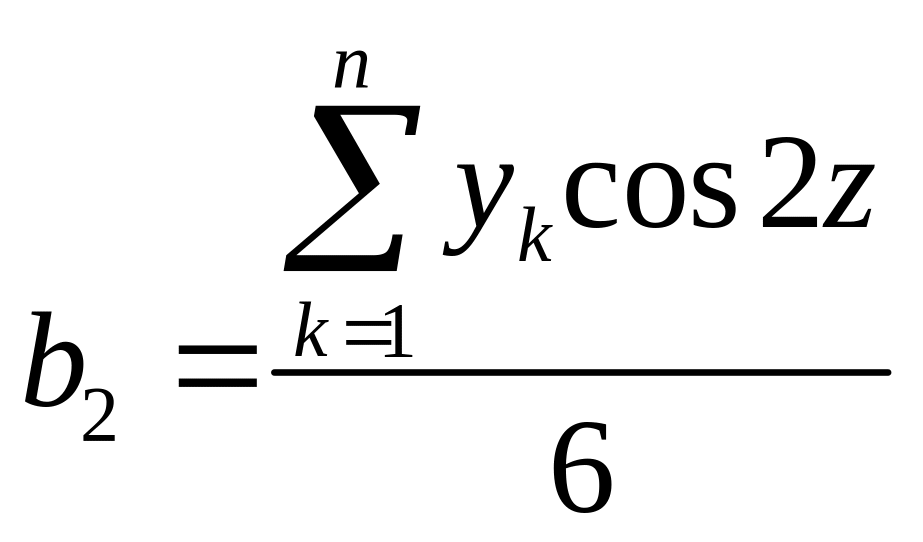Кількість гармонік k, яка включається в математичну модель, визначається мінімальним значенням основної похибки моделі
,
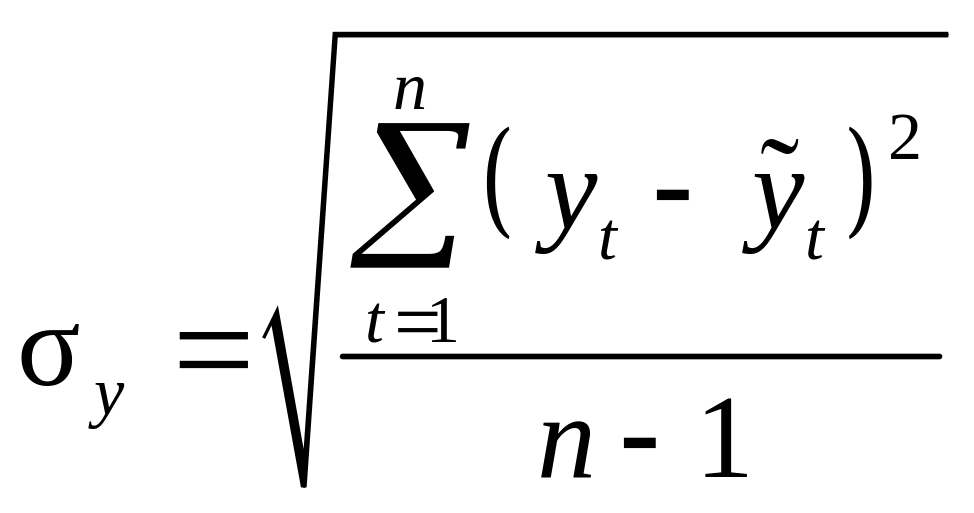(2.5)
де yt – фактичні значення показника;
– теоретичні
значення показника, обчислені з
використанням гармонічного ряду;
п – кількість спостережень.