
- •Тема 1. Вероятностные пространства 30
- •Тема 2. Основные вероятностные схемы испытаний 60
- •Тема 3. Случайные величины 87
- •Тема 4. Математическая статистика 140
- •Введение Место теории вероятностей и математической статистики в современной математической науке и их роль в экономических исследованиях
- •Особенности изучения теории вероятностей и математической статистики менеджером
- •Краткие сведения
- •Тема 1. Вероятностные пространства Лекция 1. Пространство случайных событий
- •Основные понятия теории вероятностей
- •Случайные события
- •Понятие случайного эксперимента
- •Пространство элементарных событий
- •Наступление события, благоприятствующие исходы
- •Совместные (совместимые), несовместные (несовместимые) события
- •Достоверное и невозможное события
- •Алгебра событий Операции над событиями (сумма, разность, произведение)
- •Свойства операций над событиями
- •Алгебра и сигма-алгебра событий
- •Общее определение вероятности
- •Классическое определение вероятности события. Случаи равновероятных исходов
- •Статистическое определение вероятности события. Случаи неравновероятных исходов
- •Геометрические вероятности
- •Аксиоматическое построение теории вероятностей
- •, Т.Е. Вероятность достоверного события равна единице;
- •Вероятность события , заключающееся в том, что наступит одно из попарно несовместных событий ( ), составляет
- •Полная группа событий
- •Условная вероятность
- •Формула умножения вероятностей
- •Формула сложения вероятностей
- •Независимость событий
- •Простейшие свойства вероятностей
- •Свойства условных вероятностей
- •Формула полной вероятности. Формула Байеса
- •Контрольные вопросы к теме №1
- •Тема 2. Основные вероятностные схемы испытаний Лекция 2. Основные формулы вычисления вероятностей
- •Классическая вероятностная схема
- •Правила суммы и произведения
- •Схемы выбора. Основные понятия комбинаторики
- •Выбор без возвращения, с учетом порядка
- •Выбор без возвращения, без учета порядка
- •Выбор с возвращением и с учетом порядка
- •Выбор с возвращением и без учета порядка
- •Урновая схема
- •Наивероятнейшее число наступления событий в схеме Бернулли
- •Предельные теоремы для схемы Бернулли
- •Локальная теорема Муавра–Лапласа
- •Интегральная теорема Муавра – Лапласа
- •Теорема Пуассона
- •Понятие потока событий
- •Полиномиальная схема
- •Понятие цепи Маркова
- •Однородные цепи Маркова
- •Равенство Маркова
- •Предельные вероятности
- •Контрольные вопросы к теме №2
- •Тема 3. Случайные величины Лекция 3. Одномерные случайные величины
- •Непрерывные и дискретные случайные величины
- •Закон распределения случайной величины
- •Функция распределения случайной величины и ее свойства
- •Свойства функции распределения
- •Числовые характеристики непрерывных случайных величин Математическое ожидание случайной величины, его вероятностный смысл и свойства
- •Свойства математического ожидания
- •Дисперсия случайной величины и ее свойства
- •Среднеквадратическое отклонение
- •Начальные и центральные моменты
- •Основные примеры распределений дискретной случайной величины
- •Биномиальное распределение, его математическое ожидание, дисперсия
- •Распределение Пуассона
- •Геометрическое распределение
- •Непрерывные случайные величины Функция и плотность распределения вероятностей
- •Числовые характеристики непрерывных случайных величин
- •Основные примеры распределений непрерывной случайной величины Равномерное распределение
- •Показательное распределение
- •Нормальное распределение
- •Свойства функции Гаусса
- •Центральная предельная теорема
- •Вероятность попадания нормальной случайной величины в заданный интервал
- •Функция Лапласа и ее свойства
- •Вычисление вероятности заданного отклонения. Правило «трех сигм»
- •Лекция 4. Многомерные случайные величины
- •Закон распределения вероятностей двумерной случайной величины
- •Совместная функция распределения двумерной случайной величины
- •Свойства совместной функции распределения двумерной случайной величины
- •Плотность совместного распределения вероятностей непрерывной двумерной случайной величины
- •Свойства двумерной плотности вероятности
- •Условное математическое ожидание
- •Независимые случайные величины
- •Числовые характеристики системы двух случайных величин
- •Корреляционный момент
- •Коэффициент корреляции
- •Свойства коэффициента корреляции
- •Линейная регрессия. Метод наименьших квадратов
- •Распределение 2
- •Распределение Стьюдента
- •Распределение Фишера
- •Предельные теоремы теории вероятностей Закон больших чисел. Неравенство Чебышева. Теорема Чебышева
- •Контрольные вопросы к теме №3
- •Тема 4. Математическая статистика Лекция 5. Основы математической статистики
- •Выборочный метод и его основные понятия
- •Способы отбора
- •Вариационный ряд для дискретных и непрерывных случайных величин
- •Полигон и гистограмма
- •Эмпирическая функция распределения и ее свойства
- •Свойства эмпирической функции распределения
- •Статистические оценки параметров распределения. Состоятельность и несмещенность статистических оценок
- •Выборочные среднее и дисперсия
- •Надежность и доверительный интервал
- •Определение доверительных интервалов Доверительный интервал для математического ожидания нормального распределения при известной дисперсии
- •Доверительный интервал для математического ожидания нормального распределения при неизвестной дисперсии
- •Доверительный интервал для оценки среднего квадратического отклонения нормального распределения
- •Проверка статистических гипотез
- •Статистический критерий
- •Критическая область. Область принятия гипотезы. Критические точки
- •Критерий согласия Пирсона о виде распределения
- •Элементы теории корреляции
- •Выборочные уравнения регрессии
- •Линейная регрессия
- •Множественная линейная регрессия
- •Нелинейная регрессия
- •Логарифмическая модель
- •Обратная модель
- •Степенная модель
- •Показательная модель
- •Цепи Маркова Цепи Маркова с дискретным временем
- •Однородные цепи Маркова
- •Переходные вероятности. Матрица перехода
- •Равенство Маркова
- •Цепи Маркова с непрерывным временем
- •Уравнения Колмогорова
- •Финальные вероятности состояний системы
- •Предельные вероятности
- •Контрольные вопросы к теме №4
- •Экзаменационные вопросы
- •Литература
- •Теория вероятностей и математическая статистика Курс лекций
- •220007, Г. Минск, ул. Московская, 17.
Финальные вероятности состояний системы
Если
процесс, протекающий в системе, длится
достаточно долго, то имеет смысл говорить
о предельном поведении вероятностей
при
![]() .
В некоторых случаях существуют финальные
(предельные) вероятности состояний:
.
В некоторых случаях существуют финальные
(предельные) вероятности состояний:
![]() ,
,
![]() .,
.,
не зависящие от того, в каком состоянии
система находилась в начальный момент.
Говорят, что в системе устанавливается
предельный стационарный режим,
при котором она переходит из состояния
в состояние, но вероятности состояний
![]() уже не меняются во времени.
Система, для которой существуют финальные
состояния, называется эргодической,
а соответствующий случайный процесс –
эргодическим.
уже не меняются во времени.
Система, для которой существуют финальные
состояния, называется эргодической,
а соответствующий случайный процесс –
эргодическим.
Финальные
вероятности системы могут быть получены
путем решения системы линейных
алгебраических уравнений,
которые получаются из дифференциальных
уравнений Колмогорова, если приравнять
производные к нулю, а вероятностные
функции состояний
в правых частях уравнений Колмогорова
заменить на неизвестные финальные
вероятности
![]() .
.
Таким
образом, для системы с
![]() состояниями получается система
линейных однородных алгебраических
уравнений с
неизвестными
,
которые можно найти с точностью до
постоянного множителя. Для нахождения
их точных значений к уравнениям добавляют
нормировочное условие
состояниями получается система
линейных однородных алгебраических
уравнений с
неизвестными
,
которые можно найти с точностью до
постоянного множителя. Для нахождения
их точных значений к уравнениям добавляют
нормировочное условие
![]() ,
пользуясь которым можно выразить любую
из вероятностей через другие и отбросить
одно из уравнений.
,
пользуясь которым можно выразить любую
из вероятностей через другие и отбросить
одно из уравнений.
Р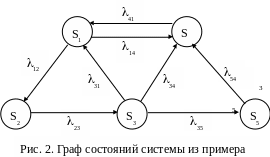 ассмотрим
следующий пример. Имеется размеченный
граф состояний системы
(рис.2). Необходимо составить систему
дифференциальных уравнений Колмогорова
и записать начальные условия для решения
этой системы, если известно, что в
начальный момент система находилась в
состоянии
ассмотрим
следующий пример. Имеется размеченный
граф состояний системы
(рис.2). Необходимо составить систему
дифференциальных уравнений Колмогорова
и записать начальные условия для решения
этой системы, если известно, что в
начальный момент система находилась в
состоянии
![]() .
.

Решение. Согласно приведенному выше мнемоническому правилу, система дифференциальных уравнений Колмогорова имеет вид:

Начальные
условия при
![]() :
:
![]() .
.
При
![]() функции
стремятся к предельным (финальным)
вероятностям состояний системы. Поскольку
финальные вероятности не зависят от
времени, в системе дифференциальных
уравнений Колмогорова все левые части
принимаем равными нулю. При этом система
дифференциальных уравнений превратится
в систему линейных алгебраических
уравнений вида:
функции
стремятся к предельным (финальным)
вероятностям состояний системы. Поскольку
финальные вероятности не зависят от
времени, в системе дифференциальных
уравнений Колмогорова все левые части
принимаем равными нулю. При этом система
дифференциальных уравнений превратится
в систему линейных алгебраических
уравнений вида:

Решая
ее с учетом условия
![]() ,
получим все предельные вероятности.
Эти вероятности представляют собой
среднее относительное время пребывания
системы в каждом из состояний.
,
получим все предельные вероятности.
Эти вероятности представляют собой
среднее относительное время пребывания
системы в каждом из состояний.
Финальные состояния марковской системы с непрерывным временем существуют при следующих условиях:
плотности вероятности всех переходов не должны зависеть от времени
 ;
;из любого состояния системы возможен переход в любое другое состояние за конечное число шагов.
Например, для системы, изображенной на рис. 3, финальные вероятности не существуют.
В заключение рассмотрим одну из наиболее простых и часто встречающихся на практике разновидностей дискретных марковских цепей с непрерывным временем – так называемую схему гибели и размножения.

Схема гибели и размножения
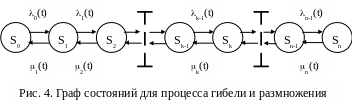
Марковский
процесс с дискретными состояниями
называется процессом гибели и
размножения, если все состояния
можно вытянуть в цепочку, в которой
каждое из промежуточных состояний
![]() может переходить только в соседние
состояния, а крайние состояния
может переходить только в соседние
состояния, а крайние состояния
![]() переходят лишь в состояния
и
переходят лишь в состояния
и
![]() соответственно. Граф состояний такой
системы приведен на рис.4.
соответственно. Граф состояний такой
системы приведен на рис.4.
Название
схемы взято из биологических задач, где
состояние популяции
![]() означает наличие в ней
особей.
означает наличие в ней
особей.
На рис.4
переход вправо соответствует увеличению
популяции, влево – ее уменьшению. Таким
образом, можно определить
![]() как интенсивности размножения, а
как интенсивности размножения, а
![]() – как интенсивности гибели. Используется
следующее соглашение: буквам
и
– как интенсивности гибели. Используется
следующее соглашение: буквам
и
![]() приписывается индекс того состояния,
из которого выходит стрелка.
приписывается индекс того состояния,
из которого выходит стрелка.
Марковским процессом гибели и размножения с непрерывным временем называется такой случайный процесс, исследуемый параметр которого может принимать только целые неотрицательные значения. Изменения рассматриваемого параметра могут происходить в любой момент времени, т.е. в любой момент времени он может либо увеличиться, либо уменьшиться на единицу.
Процессом чистого размножения называется такой процесс, у которого интенсивности всех потоков гибели равны нулю; аналогично процессом чистой «гибели» называется процесс, у которого равны нулю интенсивности всех потоков размножения.
Предельные (финальные) вероятности состояний для простейшего эргодического процесса гибели и размножения, находящегося в стационарном режиме, определяются по следующим формулам:

В качестве примера решения системы уравнений схемы гибели и размножения рассмотрим эксплуатацию автомобилей в крупной транспортной фирме.
Интенсивность
поступления автомобилей на предприятие
равна
![]() .
Каждый поступивший на предприятие
автомобиль списывается через случайное
время
.
Каждый поступивший на предприятие
автомобиль списывается через случайное
время
![]() .
Срок службы автомобиля
распределен по показательному закону
с параметром
.
Процесс эксплуатации автомобилей
является случайным процессом.
.
Срок службы автомобиля
распределен по показательному закону
с параметром
.
Процесс эксплуатации автомобилей
является случайным процессом.
![]() – число автомобилей данной марки,
находящихся в эксплуатации в момент
времени
.
– число автомобилей данной марки,
находящихся в эксплуатации в момент
времени
.
Рассмотрим два случая: 1) нет ограничений на число эксплуатируемых автомобилей, 2) на предприятии может эксплуатироваться не более автомобилей.
Если в
начальный момент
![]() на предприятии не было ни одного
автомобиля, то решать систему уравнений
нужно при начальных условиях:
на предприятии не было ни одного
автомобиля, то решать систему уравнений
нужно при начальных условиях:
![]() .
.
Аналогично, если при эксплуатировалось автомобилей, то начальные условия имеют вид:
![]()
Решение системы дифференциальных уравнений Колмогорова при произвольном виде функции не может быть найдено в аналитическом виде. Однако при постоянных интенсивностях потоков гибели и размножения и конечном числе состояний будет существовать стационарный режим. Система в этом случае является простейшей эргодической системой.
Если интенсивности потока поступления и списания автомобилей постоянны, то оказываются справедливы формулы:
1. Максимальное число автомобилей не ограничено:
 .
.
2. Математическое ожидание (среднее значение) числа эксплуатируемых автомобилей:
![]() ;
;
При ограниченном

В этом случае математическое ожидание равно:

