16. Сущность средних величин и правила их применения
Средняя величина – обобщающая количественная характеристика признака в статистической совокупности в конкретных условиях места и времени.
Сущность средней величины состоит в том, что через единичное и случайное выявляется общее и необходимое, выявляется тенденция и закономерность в развитии массовых явлений. Средняя отображает что-то общее, которое складывается в определенном единичном объекте. В средней величине отражается характерный, типичный, реальный уровень изучаемых явлений. Задачей средних величин является характеристика этих уровней и их изменений во времени и пространстве.
Условия применения средних величин:
• качественная однородность изучаемой совокупности;
• совокупность должна включать большое число факторов (событий), т.к. только в ней может проявиться закон больших чисел, обеспечивающий устойчивость средних.
Средние величины применяются: • для оценки достигнутого уровня изучаемого показателя, при анализе и планировании производственно-хозяйственной деятельности предприятий (объединений), фирм, банков и других хозяйственных единиц; • при выявлении взаимосвязей явлений, при прогнозировании, а также расчете нормативов.
Расчет средних величин необходим для:
• характеристики типичного уровня по данной совокупности;
• сравнения типичных уровней по 2 и более совокупностям;
• как нормы при установлении плановых заданий, уровней договорных обязательств.
В зависимости от характера первичных данных, области применения и способа расчета в статистике различают следующие основные виды средних: средняя арифметическая, средняя гармоническая, средняя геометрическая и средняя квадратическая.
17. Средняя арифметическая величина. Ее свойства и способы вычисления
Средняя арифметическая – такое среднее значение признака, при вычислении которого общий объем признака в совокупности сохраняется неизменным (это среднее слагаемое). Для того чтобы определить среднюю арифметическую, необходимо иметь ряд вариантов (х) и частот (f).
Средняя арифметическая бывает простая и взвешенная.
Средняя
арифметическая простая
применяется, если отдельное значение
признака встречается 1 раз или одинаковое
число раз. Она равна сумме отдельных
значений признака (хi),
деленной на число этих значений (n):
.
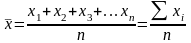Средняя
арифметическая взвешенная
используется если значения признака
(варианты) встречаются неодинаковое
число раз, то:
,
где хi
– варианты
значений признака, fi
– частота.
Основные свойства средней арифметической:
1. От уменьшения или увеличения частот каждого значения признака х в n раз величина средней арифметической не изменится. Если все частоты разделить или умножить на какое-либо число, то величина средней не изменится.
2. Общий множитель индивидуальных значений признака может быть вынесен за знак средней:
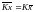
3. Средняя суммы (разности) двух или нескольких величин равна сумме (разности) их средних:
4. Если х
= с, где с
– постоянная величина, то
.
5. Сумма отклонений
значений признака x
от средней арифметической х
равна нулю:
