Лабораторная работа № 3 Тема: Измерение модуля упругости (модуля Юнга) резины

Цель: опытным путем измерить модуль Юнга резины и сравнить полученный результат с табличным.

Средства измерения: динамометр, штангенциркуль, линейка.

Оборудование: штатив с муфтой и лапкой, резиновый шнур, грузы массой по 100 г.

Теоретические сведения:

Модуль Юнга определяется из закона Гука по формуле:

E - модуль Юнга (Па);

F - сила упругости, возникающая в

растянутом шнуре и равная весу

п

рикрепленных к шнуру грузов (Н);

S - площадь поперечного сечения деформированного шнура (м²);

l₀ - расстояние между метками А и В на нерастянутом шнуре (м);

l - расстояние между этими же метками на растянутом шнуре (м).

1.Если поперечное сечение шнура имеет форму круга, то площадь поперечного сечения выражается через диаметр шнура:

π=3,14

D – диаметр шнура, измеренный штангенциркулем (м).

2. Если поперечное сечение шнура имеет форму прямоугольника, то площадь (S) вычисляется по формуле:

,

a-длина прямоугольника (измеряется линейкой) (м);

b-ширина прямоугольника (измеряется штангенциркулем) (м).

Расчетные формулы:

Для шнура, имеющего круглого сечения:

E_пр =

Для шнура, имеющего прямоугольное сечение:

E_пр =

Ход работы:

1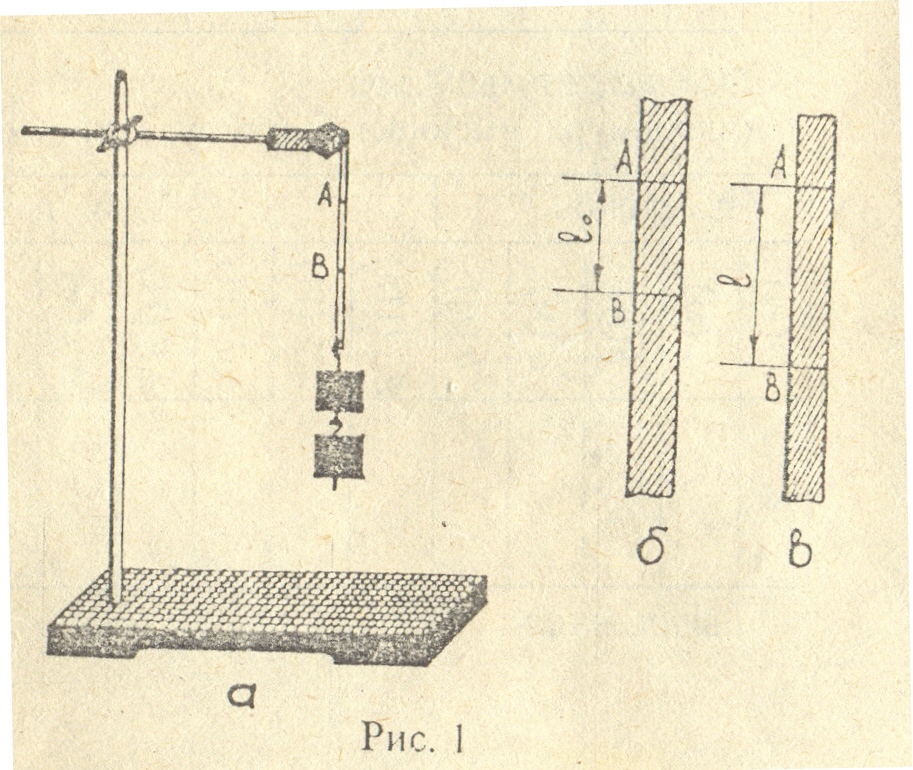 .Собираем экспериментальную установку, изображенную на рисунке 1а.

2. На резиновой шнур наносим карандашом (ручкой) метки А и В. Между метками линейкой измеряем расстояние (l_o) (см. рис.1б).

3.К нижнему концу шнура подвешиваем грузы. Вес грузов определяем предварительно с помощью динамометра. Это будет значение силы (F).

4.Измеряем расстояние (l) между метками на растянутом шнуре (см. рис. 1в).

5. Если шнур имеет круглое сечение, то измеряем диаметр шнура (D) штангенциркулем.

Если шнур имеет прямоугольное сечение, то измеряем его длину (а) линейкой и ширину (b) штангенциркулем в растянутом состоянии.

6. Модуль Юнга вычисляем с помощью расчетной формулы, результат сравниваем с табличным значением модуля Юнга для резины.

7. Результаты измерений и вычислений заносим в таблицу.

Таблица результатов

(для шнура, имеющего круглое сечение):

Измерено

В ы ч и с л е н о

F(H)

l0(м)

l(м)

D(м)

Епр(Па)

∆иF(Н)

∆0F(H)

∆F(H)

∆иl(м)

∆0l(м)

∆l(м)

∆иD(м)

∆oD(м)

∆D(м)

εЕ(%)

∆E(Па)

Таблица результатов

(для шнура, имеющего прямоугольное сечение):

Измерено

В ы ч и с л е н о

F(H)

l0(м)

l(м)

a (м)

b (м)

Епр(Па)

∆иF(Н)

∆0F(H)

∆F(H)

∆иl(м)

∆0l(м)

∆l(м)

∆иb(м)

∆ob(м)

∆b(м)

εЕ(%)

∆E(Па)

Вычисления: