2.3. Байес формуласы

Ықтималдықтарды көбейту теоремасы және толық ықтималдықтық формуласының салдары ретінде Бейес формуласы деп аталатын формуланы келтіріп шығарайық.

Толық жиын құратын өзара үйлесімсіз H₁ ,H₂,…,H_n оқиғалары берілген. H₁ ,H₂,…,H_n оқиғалар болжам, гипотеза деп те аталады. Бұл гипотезалардың тәжірибеге дейінгі ықтималдықтары белгілі болып, олар сәйкес сандарына тең болсын. Тәжірибе жүргізіліп, оның нәтижесінде қандай да А оқиғасы жүзеге асты делік. А оқиғасының пайда болуына байланысты болжам ықтималдықтары қалай өзгереді, соны қарастырайық.

Басқаша айтқанда: ,

шартты ықтималдықтарды табайық.

Ықтималдықдарды көбейту теоремасы бойынша:

Бұдан ,

немесе

Мұндағы P(A)-ны толық ықтималдықтың формуласымен алмастырайық:

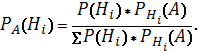
Бұл формула Байес формуласы деп аталады.

3 мысал. Екі атқыш бір-біріне тәуелсіз бір нысанаға әрқайсысы бір реттен атады. Бірінші атқыштың нысанаға тигізу ықтималдығы 0,8 , реттен екіншісікі 0,4. Ату таусылғаннан кейін нысанада бір тесік табылған (А оқиғасы). Осы тесіктің бірінші атқышқа тиісті болу ықтималдылығын табайық.

Шешімі: Тәжірибеге дейін мынадай гипотелазалар болуы мүмкін: Н₁ ̶ бірінші атқыштікі де, екінші атқыштікі де тимейді: Н₂ ̶ екі атқыштікіде тиеді; біріншінікі тиеді, екіншінікі тимейді;

Оқиғалардың толық тобын құрайтын бір-бірімен үйлеспейтін оқиғалардың біреуі А оқиғасынан орындалатын болса. Онда А оқиғасының ықтималдығы:

формуласымен анықталады, мұнда Р(В₁А),... бір-бірімен үйлеспейтін оқиғалардың ықтималдығы теңдеулермен анықталады.

4 мысал. Складта әр заводтан келген магнитофондар бар.

№1-ден – 12, №2 – 20, №3 – 18. №1-ден келген магнитофондардың сапасы өте жоғары екендігінің ықтималдығы 0,9, №2, №3-тікі Р(В₂)=0,6 және Р(В₃)=0,9.

Складтан алынған магнитофонның сапасы өте жоғары екендігінің ықтималдығын табыңдар.

Шешуі: А-ден алынған заттың сапасы өте жоғары екендігінің оқиғасы. - №1, №2, №3 заводтарындағы жасалған заттар. -бір-бірімен байланыссыз оқиғалар А оқиғасының орындалуы болып саналады. ( ) – №1 заводта жасалған магнитофонның сапасы өте жоғары екендігін көрсетеді):

Р( )=Р( )·Р_в(А), Р( )=Р( )·Р_в(А), Р( )=Р( )·Р_в(А).

Жауабы: Р(А)=0,78.

2.4. Байланыссыз қайталанатын сынау

Егер А оқиғасының ықтималдығы әр сынаудың нәтижесінде байланыссыз болса, онда ондай сынауларды А оқиғасына қарағанда бір-бірімен байланыссыз сынаулар деп атаймыз.

Есептің шарты: n байланыссыз сынаудың нәтижесінде А оқиғасы m рет пайда болады дегеннің ықтималдығын табу керек, егер әр сынауда осы оқиға белгіленген ықтималдықпен Р(А)=р, (Р( )=1-р-q) пайда болады десек.

Енді Бернулли формуласымен қолданамыз: n сынау кезінде А оқиғасының n рет пайда болуы немесе 0, немесе 1, немесе 2,... толық оқиғасының қатарын құрайды,

яғни _.

Бұл ықтималдықтың биномальдық орналасуы деп аталады, өйткені (q+p)ⁿ ̶ биномының мүшелерімен сәйкес келеді.