20. Правило Лопиталя. Первое правило Лопиталя

Рассмотрим функции , которые бесконечно малЫ в некоторой точке . Если существует предел их отношений , то в целях устранения неопределённости  можно взять две производные – от числителя и от знаменателя. При этом: , то есть при дифференцировании числителя и знаменателя значение предела не меняется.

Примечание: предел  тоже должен существовать, в противном случае правило не применимо.

Второе правило Лопиталя

Брат-2 борется с двумя спящими восьмёрками . Аналогично:

Если существует предел отношения бесконечно больших в точке  функций: , то в целях устранения неопределённости  можно взять две производные – ОТДЕЛЬНО от числителя и ОТДЕЛЬНО от знаменателя. При этом: , то есть при дифференцировании числителя и знаменателя значение предела не меняется.

Примечание: предел  должен существовать

Опять же, в различных практических примерах значение  может быть разным, в том числе, бесконечным. Важно, чтобы была неопределённость .

<Вернуться назад>

21. Многочлен Тейлора, формула Тейлора.

Рассмотрим многочлен -й степени

Его можно представить в виде суммы степеней , взятых с некоторыми коэффициентами. Продифференцируем его раз по переменной , а затем найдем значения многочлена и его производных в точке :

Таким образом, получаем, что

Полученное выражение называется формулой Маклорена для многочлена  степени .

Рассуждая аналогично, можно разложить многочлен  по степеням разности , где  - любое число. В этом случае будем иметь:

Это выражение называется формулой Тейлора для многочлена  в окрестности точки .

Пример

Задание. Разложить в ряд Тейлора функцию  в точке .

Решение. Найдем производные:

Итак, , , . Значение функции в точке

Таким образом,

Ответ. 

Для произвольной функции , не являющейся многочленом, формула Тейлора в окрестности некоторой точки принимает вид:

Последнее слагаемое  называется остаточным членом в форме Пеано.

Замечание

Формула Маклорена является частным случаем формулы Тейлора при .

<Вернуться назад>

22. Остаточный член формулы Тейлора в формах Пеано и Лагранжа.

Формула Тейлора с остаточным членом в форме Пеано. Пусть функция f: [a, b] → R имеет в точке x0 производную n-го порядка. Тогда при x → x0

Если x0 = a или x0 = b, то под производными понимаются соответствующие односторонние производные.

Формула Тейлора с остаточным членом в форме Лагранжа имеет вид

<Вернуться назад>

23. Локальный экстремум функции одного переменного. Необходимое и достаточное условия экстремума.

Определение

Точка  называется точкой локального максимума функции , если существует такая окрестность этой точки, что для всех  из этой окрестности выполняется неравенство: .

Точка  называется точкой локального минимума функции , если существует такая окрестность этой точки, что для всех  из этой окрестности .

Наибольшее или наименьшее значение функции на промежутке называется глобальным экстремумом.

Замечание

Глобальный экстремум может достигаться либо в точках локального экстремума, либо на концах отрезка.

Теорема

(Необходимое условие экстремума)

Если функция  имеет экстремум в точке , то ее производная  либо равна нулю, либо не существует.

Точки, в которых производная равна нулю: , называются стационарными точками функции.

Точки, в которых выполняется необходимое условие экстремума для непрерывной функции, называются критическими точками этой функции. То есть критические точки - это либо стационарные точки (решения уравнения ), либо это точки, в которых производная  не существует.

Замечание

Не в каждой своей критической точке функция обязательно имеет максимум или минимум.

Теорема

(Первое достаточное условие экстремума)

Пусть для функции  выполнены следующие условия:

1. функция непрерывна в окрестности точки ;

2.  или 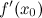 не существует;

3. производная  при переходе через точку  меняет свой знак.

Тогда в точке  функция  имеет экстремум, причем это минимум, если при переходе через точку  производная меняет свой знак с минуса на плюс; максимум, если при переходе через точку  производная меняет свой знак с плюса на минус.

Если производная  при переходе через точку  не меняет знак, то экстремума в точке  нет.

Таким образом, для того чтобы исследовать функцию  на экстремум, необходимо:

1. найти производную ;

2. найти критические точки, то есть такие значения , в которых  или  не существует;

3. исследовать знак производной слева и справа от каждой критической точки;

4. найти значение функции в экстремальных точках.

Пример

Задание. Исследовать функцию  на экстремум.

Решение. Находим производную заданной функции:

Далее ищем критические точки функции, для этого решаем уравнение :

Первая производная определена во всех точках. Таким образом, имеем одну критическую точку . Наносим эту точку на координатную прямую и исследуем знак производной слева и справа от этой точки (для этого из каждого промежутка берем произвольное значение и находим значение производной в выбранной точке, определяем знак полученной величины):

Так как при переходе через точку  производная сменила свой знак с "-" на "+", то в этой точке функция достигает минимума (или минимального значения), причем .

Замечание. Также можно определить интервалы монотонности функции: так как на интервале производная , то на этом интервале функция  является убывающей; на интервале  производная , значит заданная функция возрастает на нем.

Ответ. 

Теорема

(Второе достаточное условие экстремума)

Пусть для функции  выполнены следующие условия:

1. она непрерывна в окрестности точки ;

2. первая производная  в точке ;

3.  в точке  .

Тогда в точке  достигается экстремум, причем, если , то в точке  функция имеет минимум; если , то в точке  функция  достигает максимум.

<Вернуться назад>