15. Таблица производных.
<Вернуться назад>
16. Производные сложной и обратной функции.
-
Таблица производных сложной функции:
-
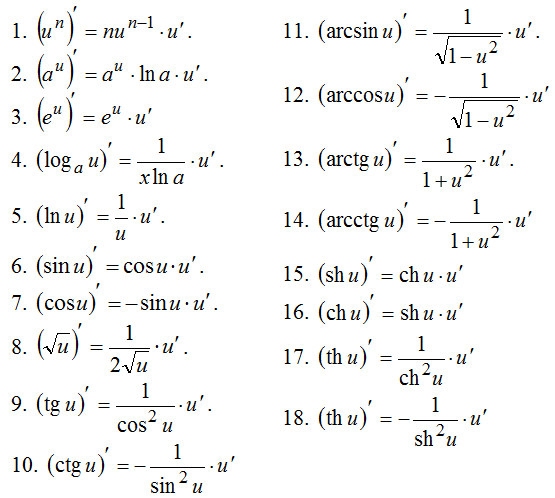
Производная обратной функции:
Если y=f(x) и x=g(y) — пара взаимно обратных функций, и функция y=f(x) имеет производную f'(x), то производная обратной функции g'(x)=1/f'(x).
Доказательство: По условию теоремы функция x = f(y) монотонна и дифференцируема, следовательно, по теореме о существовании обратной функции функция у = f--1(x) существует, монотонна и непрерывна на соответствующем интервале. Дадим аргументу х приращение Δх¹0. Тогда функция у = f--1(x) получит приращение Δу, которое в силу ее монотонности отлично от нуля. Так как функция у = f--1(x) непрерывна, то Δу®0 при Δх®0.
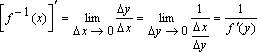
Тогда
<Вернуться назад>
17. Дифференциал, его связь с производной, геометрический смысл, инвариантность.
Дифференциалом
в
точке x, соответствующему
называется
главная линейная
часть приращения функции.
.
То есть если существует
производная, то
при
,
и дифференциал
.
Когда x=const,
то переменной является
и дифференциал будет линейной функцией.
геометрический
смысл дифференциала:
дифференциал функции
в точке
равен приращению ординаты касательной
к графику функции в этой точке, когда
получит приращение
Инвариантность формул первого дифференциала
Пусть существует сложная
функция
,
и существует ее производная:
.
Считая y
независимой переменной, получим формулу
дифференциала:
.
Теперь, если считать y
зависимой от x,
получим:
,
т.к.
.
То есть получается, что формула
дифференциала не зависит от типа
переменной.
<Вернуться назад>
18. Теорема Ролля, её геометрический смысл.
Пусть функция f (x) непрерывна на [a, b], дифференцируема на (a, b) и на концах отрезка принимает равные значения f(a) = f(b). Тогда существует точка c Î (a, b), в которой f ' (c) = 0.
Доказательство. Так как функция f(x) непрерывна на [a, b], то по свойству непрерывных функций она достигает на этом отрезке максимальное значение М и минимальное значение m. Возможны два случая: максимум и минимум достигаются на концах отрезка или что – либо (или максимум, или минимум) попадает вовнутрь интервала. В первом случае f (x) = const = M = m. Поэтому производная равна нулю f ' (c) = 0 в любой точке отрезка [a, b], и теорема доказана. Во втором случае, так как f (x) дифференцируема в точке c, из теоремы Ферма следует, что f ' (c) = 0.
Геометрически теорема Ролля означает, что у графика непрерывной на отрезке [a, b] и дифференцируемой внутри этого отрезка функции, принимающей на его концах f(a) = f(b) равные значения, существует точка (c; f(c)), в которой касательная параллельна оси Оx.
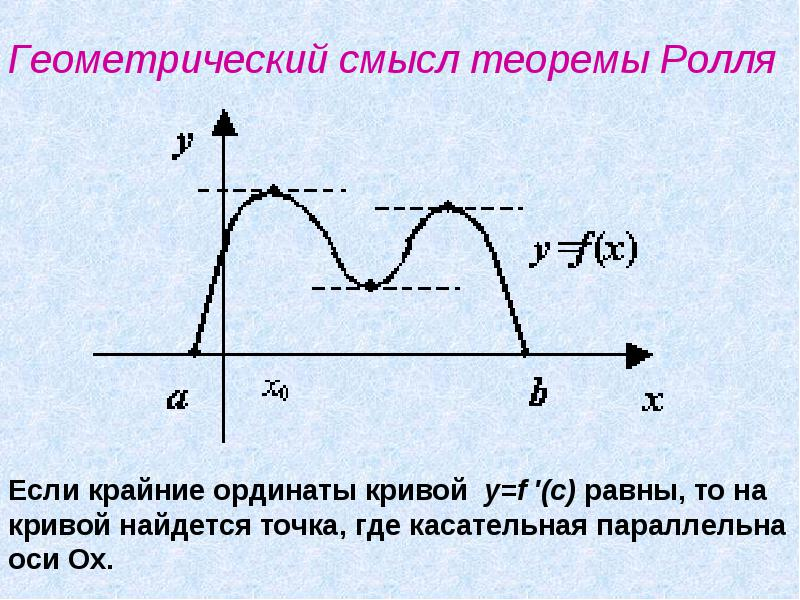
<Вернуться назад>
19. Теорема Лагранджа, ее геометрический смысл. Теорема Коши.
Пусть
функция
дифференцируема в открытом промежутке
и сохраняет непрерывность на концах
этого промежутка. Тогда существует
такая точка
,
что
|
|
|
(13) |
|
Доказательство. Рассмотрим вспомогательную функцию
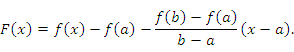
Эта
функция непрерывна и дифференцируема
в промежутке
,
а на его концах принимает одинаковые
значения:
Тогда
удовлетворяет всем условиям теоремы
Ролля и, следовательно, существует точка
,
в которой производная функции
равна нулю:
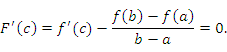
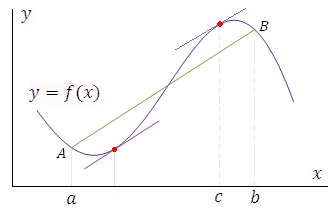
Геометрическая
интерпретация теоремы Лагранжа.
Разностное отношение в правой части
формулы (13) есть угловой коэффициент
секущей, проходящей через точки
и
,
а производная
равна угловому коэффициенту касательной
к графику функции
в некоторой средней точке промежутка
.
Поэтому за теоремой Лагранжа закрепилось
название “теорема о среднем”.
Теорема
Коши. Пусть
функции
и
непрерывны в замкнутом промежутке
;
дифференцируемы в открытом промежутке
;
в открытом промежутке
.
Тогда существует такая точка
,
что
|
|
|
Доказательство.
Заметим, что
.
В противном случае – согласно теореме
Ролля – производная
обратилась бы в нуль в некоторой точке
.
Рассмотрим вспомогательную функцию
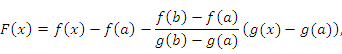
которая
удовлетворяет всем условиям теоремы
Ролля и, в частности, принимает одинаковые
значения на концах промежутка
:
Тогда
существует точка
,
в которой
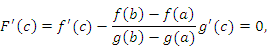
что и требовалось доказать.
<Вернуться назад>