Быстрый переход:
-
Определение предела последовательности. Подпоследовательность. Частичный предел.
-
Критерий Коши. Свойство сходящихся последовательностей. Теорема о пределе промежуточной последовательности.
-
Определение предела функции. Теорема о пределе промежуточной функции. Первый замечательный предел.
-
Бесконечно малые функции. Теорема о связи бесконечно малых и бесконечно больших функций.
(+ определение б/б функций lim f(x) = ∞)
-
Теорема о пределе произведения бесконечно малой и ограниченной функции
-
Второй замечательный предел. Раскрытие неопределенностей
-
Сравнение бесконечно малых. Эквивалентность бесконечно малых. Основные эквивалентности.
-
Теорема о разности эквивалентных бесконечно малых. Теорема о замене эквивалентности в пределе отношения.
-
Непрерывность функции в точке. Теорема о непрерывности арифметических действий. о непрерывности сложной функции.
-
Непрерывность функции на отрезке. Свойства функций непрерывных на отрезке.
-
Точки разрыва и их классификация
-
Производная, ее геометрический и механический смысл
-
Теорема о связи непрерывности и дифференцируемости
-
Арифметические действия с производными
-
Таблица производных
-
Производные сложной и обратной функции
-
Дифференциал, его связь с производной, геометрический смысл, инвариантность.
-
Теорема Ролля, ее геометрический смысл
-
Теорема Лагранджа, ее геометрический смысл. Теорема Коши.
-
Правило Лопиталя.
-
Многочлен Тейлора, формула Тейлора.
-
Остаточный член формулы Тейлора в формах Пеано и Лагранджа
-
Локальный экстремум функции одного переменного. Необходимое и достаточное условия экстремума.
-
Геометрический смысл второй производной. Точки перегиба.
-
Асимптоты графика функции. Существование наклонной асимптоты.
-
Частные производные функции нескольких переменных. Теорема о равенстве смешанных производных.
-
Дифференцируемость функции нескольких переменных. Дифференциал.
-
Локальный экстремум функции нескольких переменных. Необходимое условие экстремума.
Нахождение производных по определению 1
Нахождение производных по определению 2
<Справка>
1. Определение предела последовательности. Подпоследовательность. Частичный предел.
-
Предел числовой последовательности:
Число 
называется
пределом последовательности 
,
если для любого 
существует
номер
такой, что для любого 
выполняется неравенство 
:
-
Подпоследовательность:
Пусть
задана некоторая последовательность {
}
и
есть строго возрастающая последовательность
натуральных чисел.
Тогда
последовательность
называется
подпоследовательностью последовательности
{
}.
Будем
писать:
и
говорить, что последовательность {
}
стремится к плюс бесконечности, если
для каждого числа 
найдется
номер 
,
такой что 
при
любом 
Аналогично
даются определения для случая 
,
-
Частичный предел последовательности:
-
Частичным пределом последовательности называется предел какой-нибудь сходящейся подпоследовательности.
-
Частичным пределом последовательности называется предел какой-либо её подпоследовательности, если существует хотя бы одна подпоследовательность, имеющая предел. В противном случае, говорят, что у последовательности нет частичных пределов.
Пример:
Пусть 
Эта
последовательность расходится, но ее
подпоследовательности 
и 
сходятся
соответственно к 1 и -1.Таким образом эти
числа являются частичными пределами
последовательности 
<Вернуться назад>
2. Критерий Коши. Свойство сходящихся последовательностей. Теорема о пределе промежуточной последовательности.
-
Свойства фундаментальных последовательностей:
Если последовательность 
фундаментальная,
тогда существует такой номер 
,
что в 
-окрестности
точки 
содержатся
все члены последовательности, начиная
с этого номера.
Последовательность 
сходится тогда
и только тогда, когда она
ограниченная и верхний предел
равен нижнему.
<Вернуться назад>
3. Определение предела функции. Теорема о пределе промежуточной функции. Первый замечательный предел.
-
Предел:
-
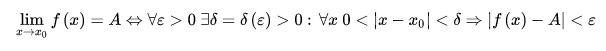
Пределпромежуточной функции
Если имеет
место соотношение 
и 
, 
,
то и 
или говорят: если
функция F(х) заключена между двумя
функциями s(х) и g(х), стремящимися к одному
и тому же пределу, то она также стремится
к этому пределу.
Пример:
Найти предел
функции 
в
точке 
,
если известно, что имеет место
соотношение: 
и
, 
Решение: Найдем
пределы заданных функций 
и 
при 
:
А тогда по теореме о предел промежуточной функции и
Ответ. 
-
Первый замечательный предел:
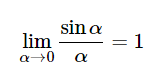
Так как при α→0 имеем sinα→0, то говорят, что первый замечательный предел раскрывает неопределённость вида 0/0. Вместо переменной α под знаком синуса и в знаменателе может быть расположено любое выражение, если:
-
Выражения под знаком синуса и в знаменателе одновременно стремятся к нулю, т.е. присутствует неопределенность вида 0/0.
-
Выражения под знаком синуса и в знаменателе совпадают.
Часто используются также
следствия из первого замечательного
предела:
<Вернуться назад>
4. Бесконечно малые функции. Теорема о связи бесконечно малых и бесконечно больших функций.
-
Бесконечно малые функции:
Функция 
называется бесконечно
малой функцией (б.м или б/м) при 
(или
в точке 
),
если
Пример:
Функция 
является
бесконечно малой (б.м) функцией при 
.
Основные свойства бесконечно малых функций:
1)Сумма конечного числа б.м функций является функцией б.м.
2)Произведение б.м функции на ограниченную есть функция б.м.
3)Произведение двух б.м функций есть функция б.м.
4)Произведение б.м функции на константу является б.м функцией.
5)Частное от деления б.м функции на функцию, предел которой не равен 0, есть функция б.м.
6)Функция 1/f(x), обратная к б.м функции, есть функция бесконечно большая. Верно и обратное.
Теорема:
Пусть 
- предел
функции 
в
точке 
: 
.
Тогда заданную функцию можно представить
в виде 
,
где 
-
б.м.
функция. Верно и обратное утверждение.
-
Теорема о связи бесконечно малых и бесконечно больших функций:
Если
функция
- функция бесконечно малая (
),
то функция
есть бесконечно большая функция и
наоборот.
Доказательство:
Пусть
- бесконечно малая функция при
,
т.е.
.
Тогда для любого числа
существует такое число
,
что для всех
,
удовлетворяющих неравенству
,
выполняется неравенство
,
т.е.
,
т.е.
,
где
.
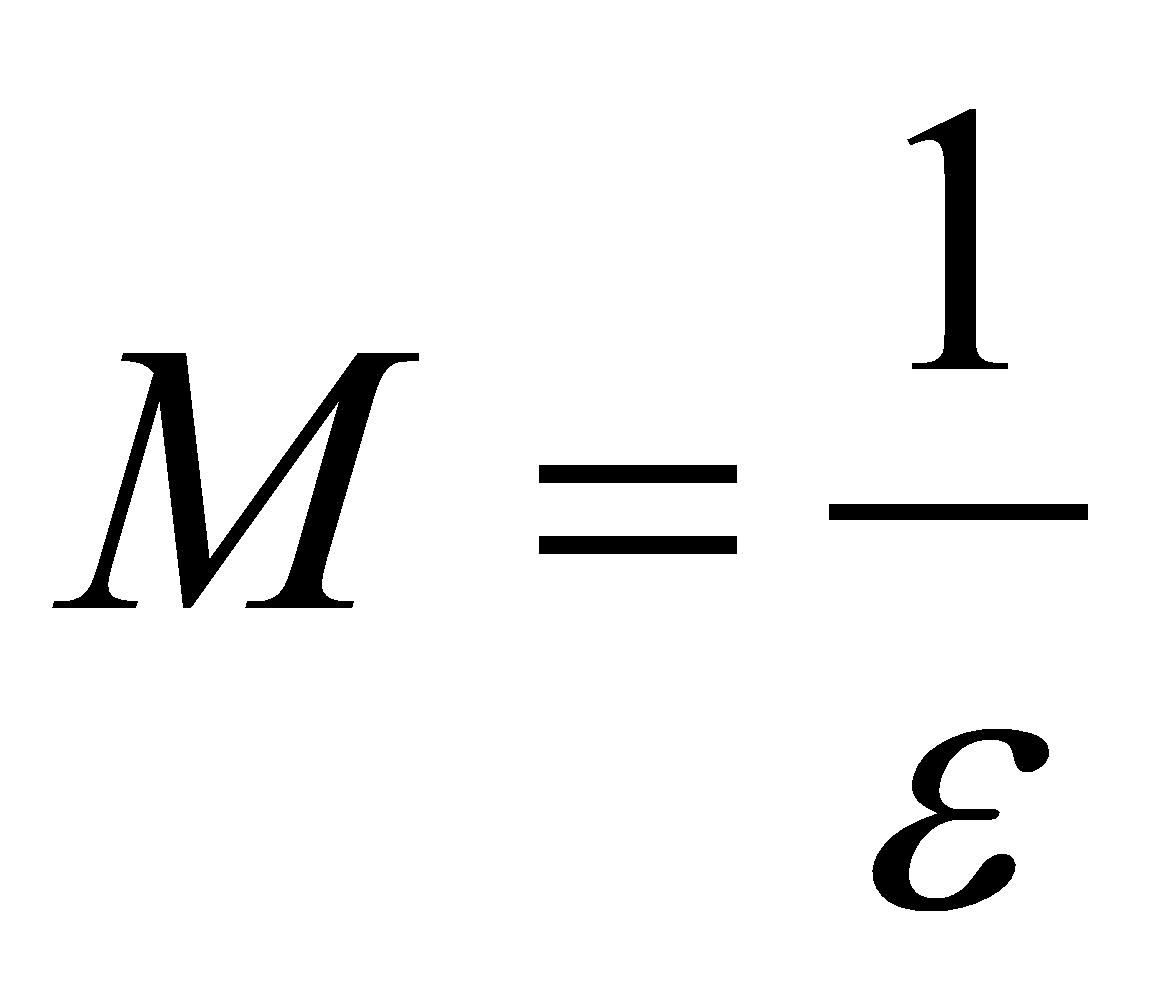А из этого следует, что функция
- бесконечно большая.
<Вернуться назад>