Замкнутые системы

Замкнутая система тел в механике — совокупность физических тел, у которых взаимодействия с внешними телами отсутствуют или скомпенсированы.

Замкнутая термодинамическая система — изолированная термодинамическая система, для которой невозможен обмен с внешней средой путем совершения работы.

Закон сохранения импульса

Зако́н сохране́ния и́мпульса (Зако́н сохране́ния количества движения) утверждает, что сумма импульсов всех тел (или частиц) замкнутой системы есть величина постоянная.

Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил. В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Однако этот закон сохранения верен и в случаях, когда ньютоновская механика неприменима (релятивистская физика, квантовая механика).

Как и любой из законов сохранения, закон сохранения импульса описывает одну из фундаментальных симметрий, — однородность пространства

№8 Второй и третий законы Ньютона Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и получающимся от этого ускорением этой точки. Фактически, второй закон Ньютона вводит массу как мерило проявления инерции материальной точки в выбранной инерциальной системе отсчёта (ИСО).

Второй закон Ньютона утверждает, что В инерциальной системе отсчета ускорение, которое получает материальная точка, прямо пропорционально приложенной к ней силе и обратно пропорционально её массе.

При подходящем выборе единиц измерения, этот закон можно записать в виде формулы:

где — ускорение материальной точки;

— сила, приложенная к материальной точке;

m — масса материальной точки.

В случае, когда масса материальной точки меняется со временем, второй закон Ньютона формулируется с использованием понятия импульс:

В инерциальной системе отсчета скорость изменения импульса материальной точки равна действующей на неё силе.

Третий закон Ньютона

Этот закон объясняет, что происходит с двумя взаимодействующими телами. Возьмём для примера замкнутую систему, состоящую из двух тел. Первое тело может действовать на второе с некоторой силой , а второе — на первое с силой . Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются.

Сам закон: Тела действуют друг на друга с силами, имеющими одинаковую природу, направленными вдоль одной и той же прямой, равными по модулю и противоположными по направлению:

№9 Центр инерции и закон его движения

геометрическая точка, положение которой характеризует распределение масс в теле или механической системе. Координаты Ц. м. определяются формулами

пpоизведение массы системы на ускоpение центpа масс pавно геометpической сумме внешних сил, действующих на тела системы. Как видим, закон движения центpа масс напоминает втоpой закон Ньютона. Если внешние силы на систему не действуют или сумма внешних сил pавна нулю, то ускоpение центpа масс pавно нулю, а cкоpость его неизменна во вpемени по модулю и напpавлению, т.е. в этом случае центp масс движется pавномеpно и пpямолинейно.

В частности, это означает, что если система замкнута и центp масс ее неподвижен, то внутpенние силы системы не в состоянии пpивести центp масс в движение. На этом пpинципе основано движение pакет: чтобы pакету пpивести в движение, необходимо выбpосить выхлопные газы и пыль, обpазующиеся пpи сгоpании топлива, в обpатном напpавлении.

ентp масс тела конечных pазмеpов в поле тяжести (если пpенебpечь сопpотивлением в воздухе) движется с ускорением свободного падения (в общем случае по паpаболе).

№10 Работа и ее выражение через криволинейный интеграл

Механическая работа (более развёрнуто: работа силы F за время Δt процесса γ(t)) — это физическая величина, являющаяся количественной характеристикой действия силы F на процесс γ(t). Если действующая сила F и вектор скорости v процесса γ за всё время наблюдения Δt постоянны, работа численно равна , в противном случае она вычисляется как интеграл:

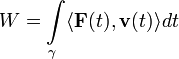Как следствие, если движение процесса ортогонально силе F, её работа равна нулю. Работа силы имеет смысл энергии, которая затрачивается источником силы (силовым полем) на своё влияние на процесс γ, и измеряется в джоулях (система СИ)

№11 Виды энергию . Потенциальная и кинетическая

Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения. Единица измерения в системе СИ - Джоуль.

Работа всех сил, действующих на частицу, идёт на приращение кинетической энергии частицы:

Потенциальная энергия — работа, которую необходимо совершить, чтобы перенести тело из некой точки отсчёта в данную точку в поле консервативных сил. Другое определение: потенциальная энергия - это функция координат, являющаяся слагаемым в лагранжиане системы, и описывающая взаимодействие элементов системы[1].

Потенциальная энергия принимается равной нулю для некоторой точки пространства, выбор которой определяется удобством дальнейших вычислений. Процесс выбора данной точки называется нормировкой потенциальной энергии. Понятно также, что корректное определение потенциальной энергии может быть дано только в поле сил, работа которых зависит только от начального и конечного положения тела, но не от траектории его перемещения. Такие силы называются консервативными.

К примеру, потенциальная энергия тела вблизи поверхности Земли рассчитывается по формуле , где m — масса тела, g - величина ускорения свободного падения, h — высота, на поверхности Земли (h = 0) величина потенциальной энергии принимается равной нулю. Здесь величина потенциальной энергии зависит только от высоты h, но не зависит от траектории, по которой тело переместилось с поверхности Земли в произвольную точку с высотой h.

Примеры полей, в которых можно ввести потенциальную энергию: поле сил всемирного тяготения, электростатическое поле, поле сил упругих деформаций и пр.

№12 Понятие о градиенте скалярной функции

Градиент (от лат. gradiens, род. падеж gradientis — шагающий) — характеристика, показывающая направление наискорейшего возрастания некоторой величины, значение которой меняется от одной точки пространства к другой. Например, если взять высоту поверхности Земли над уровнем моря (2-мерное пространство), то её градиент в каждой точке поверхности будет показывать «в горку». Смысл градиента любой скалярной функции f в том, что его скалярное произведение с бесконечно малым вектором перемещения дает полный дифференциал этой функции при соответствующем изменении координат в пространстве, на котором определена f, то есть линейную (в случае общего положения она же главная) часть изменения f при смещении на