24 Вопрос

Имеется m пунктов S₁, S₂,………….S_m производства однородного продукта (угля, цемента и т.п.), причём объем производства в пункте S_i равен a_i единиц. Произведенный продукт потребляется в пунктах Q₁, Q₂,………..,Q_n, и потребность в нем в пункте Q_j составляет b_j. (j=1,2,….., n). Требуется составить план перевозок из пунктов S_i в пункты Q_j, чтобы удовлетворить потребности в продукте b_j, не допустить затоваривания пунктов производства и минимизировать транспортные расходы.

Введем переменную x_ij, показывающую сколько единиц продукта перевозится из пункта S_i в пункт Q_j. Пусть стоимость перевозок одной единицы продукта равна с_ij. Накладывая условие линейности, будем считать, что при перевозке x_ij единиц продукта, транспортные расходы равны c_ijx_ij, т.е. предполагается, что затраты на перевозку прямо пропорциональны количеству перевозимого товара.

Назовем планом перевозок набор чисел (x_ij), i=1,2,…..,m; j=1,2,…….,n, удовлетворяющий ограничениям

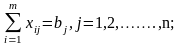
При плане перевозок (x_ij) транспортные расходы составят величину

(4)

Окончательная формулировка транспортной задачи такова: среди всех наборов чисел (x_ij), удовлетворяющих ограничениям, найти набор, минимизирующий выражение (4).

25 Вопрос

Некоторая фирма имеет n пунктов производства однородной продукции: A₁, A₂ ,…, A_n, и m пунктов потребления (рынков сбыта): B₁, B₂,…, B_m.

Предположим, что заданы величины a₁, a₂,…, a_n, b₁, b₂,…, b_m, которые определяют максимальные производительности пунктов производства и минимальные потребности пунктов потребления соответственно.

Обозначим:

c_ij – стоимость перевозок единицы продукции из пункта производства A_i в пункт потребления B_j;

x_ij – количество продукции, направляемое из пункта производства A_i в пункт потребления B_j. Совокупность чисел {x_ij} образует план перевозок.

Требуется определить такой план перевозок, который минимизирует транспортные расходы.

Транспортные расходы составят величину:

.

Неравенство

означает, что количество продукции, вывозимое из пункта производства A_i, не превосходит его максимальной производительности.

Аналогично неравенство

означает, что количество продукции, ввозимое в пункт потребления B_j, не меньше его минимальной потребности.

Таким образом, математически в транспортной задаче требуется найти план перевозок {x_ij}, который минимизирует транспортные расходы

при ограничениях

,

,

x_ij ≥ 0.

Отсюда следует, что транспортная задача является задачей линейного программирования. План перевозок x_ij назовем допустимым, если он удовлетворяет ограничениям. Допустимый план перевозок назовем оптимальным, если на этом плане транспортные расходы минимальны.

Для совместимости ограничений необходимо выполнение неравенства

,

т.е. суммарная производительность всех производств не меньше суммарного минимального потребления.

26 Вопрос

Ситуация, на основе которой обычно ставится задача о назначениях, выглядит достаточно искусственной. Поэтому целесообразность рассмотрения этой задачи объясняется в первую очередь обилием приложений, т.е. можно привести множество примеров, где возникают задачи, которые можно интерпретировать как задачи о назначениях.

В процессе управления производством зачастую возникают задачи назначения исполнителей на различные виды работ. Например, подбор кадров и назначение кандидатов на вакантные должности, распределение источников капитальных вложений между различными проектами научно – технического развития.

Задачу о назначениях можно сформулировать следующим образом. Необходимо выполнить n различных работ. Для их выполнения можно привлечь n рабочих. Каждый из рабочих готов выполнить любую работу, но эффективность использования их на различных работах неодинакова. Требуется так распределить работы между рабочими, чтобы общая эффективность выполнения ими работ была бы максимальной.

Обозначения:

c_ij – мера эффективности назначения, т.е. использования i – го рабочего на j – й работе;

x_ij – переменная задачи;

Модель задачи о назначениях:

Ограничения, отражают следующие условия:

1. каждая работа должна быть выполнена;

2. каждый рабочий может использоваться только на одной работе.

Целевая функция выражает максимум эффекта.

В каноническом виде, когда число исполнителей совпадает с количеством работ, матрица коэффициентов при переменных в ограничениях {c_ij} является квадратной.

Если количество работ меньше исполнителей, необходимо ввести дополнительные работы, чтобы матрица назначений стала квадратной. Соответствующие коэффициенты матрицы назначений можно положить равными нулю.

Задача о назначениях является задачей транспортного типа, поэтому для ее решения можно использовать методы решения транспортной задачи: метод потенциалов и венгерский метод.