17. Очікувана корисність. Теорема Наймана-Моргенштерна

Аксиоматика:

Теорема про очікувану корисність

• Теорема працює з поняттям функції корисності

• Використовує 5 аксіом (аксіома неперервності, незалежності....)

• доведення

Для доведення аксіоми незалежності використовуємо Нерівність Йєнсена - обов"язково ознайомитись

Важливий наслідок з Нерівності Йєнсена:

Якщо функція корисності g, тоді:

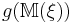•  - впевнений виграш для Того хто Приймає Рішення

•  - випадковий виграш для ТПР

Ідея в тому, що для ТПР що опуклі (їх функція увігнута вниз) вибір буде за випадковий виграш, для увігнутих ТПР (їх функція увігнута вгору) вибір буде за впевнений виграш.

Тобто, для перших: 

Для других: 

18. Функція втрат. Невід’ємна функція витрат

Згадаємо поняття корисності та функції корисності, а вже від цього зробимо визначення функції втрат.

На множині нехай задано функцію корисності . Вважається, що функція може бути виміряна відносно існуючої алгебри підмножин .Для будь якого фіксованого рішення функція індукує імовірнісний розподіл на множині доходів . При будь якому значення визначається наступним чином .

Для цього необхідне виконання наступних умов : при будь якому множина належить алгебрі . Припустимо, що дана умова виконується для будь якого рішення . Тоді для будь якого імовірнісного розподілу , для якого функція є інтегрованою, середню корисність можно обрахувати за формулою

Коли рішення приймається без інформації про стан експерименту, називається параметром, а множина параметричним простором. В задачах рішення зазвичай кожному рішенню прийнято співставляти не корисність, як це робилось раніше, а втрати, що мають за сутність від’ємну корисність. Більш точно для всіх станів та всіх рішень втрати визначаються рівністю :

Видно, що задача рішень визначається параметричним простором , простором рішень та дійсною функцією втрат , що задана на декартовому добутку . Нехай імовірнісний розподіл параметру . При будь якому рішенні середні втрати , що називаються ризиком, визначаються за формулою

Слід зауважити, що інтеграл дискретний при всіх . Статистик має намагатися прийняти рішення яке буде мінімізувати ризик .

Невід’ємність втрат :

Нехай розподіл параметру в деякій задачі рішення є . Нехай далі є деяка стала, та - дійсна функція на параметричному просторі така, що інтеграл

(17.1)

дискретний. Розглянемо тоді нову функцію втрат , що визначена за початковою функцією втрат, та вона виглядає так : , Для будь якого рішення нехай позначує ризик, що відповідає початковій функції втрат , а - ризик, що відповідає новій функції втрат . Тоді для будь яких рішень відношення та рівносильні. Тобто рішення є тоді тільки баєсівським рішенням за розподілу для початкової функції, коли це рішення є баєсівським рішенням і для нової функції втрат, за того ж розподілу. Розглянемо тепер функцію , що задана для всіх формулою

Якщо інтеграл від функції задовольняє умові (17.1), то ми можемо замінити новою функцією втрат , що визначена для всіх параметрів та рішень рівністю

Функція має наступні властивості :для всіх параметрів та рішень, що належать відповідних просторам маємо :

та . В багатьох задачах зручніше мати справу з не від’ємними функціями втрат вказаного вигляду, хоча і здається, що в цьому випадку і здається, що у даному випадку статистик завжди приймає рішення, що не дає позитивного виграшу.

Функція втрат L(ω, d), задана на Ω X D. При будь-якому (ω,d)   Ω X D число

L(ω, d) – втрата статистика при прийнятті рішення d у випадку, коли значення параметра Ω = ω.

Вважаємо, що L( , d) при всіх d   D є А-вимірною функцією над простором Ω.

(X, F) і (Y, G) – дві множини з виділеними сигма-алгебрами підмножин.

Тоді функція f: X   Y називається F/G-вимірною, якщо повний прообраз довільної множини з G належить F.

Тобто ∀ B ∈ G: f ^-1 (B) ∈ F.

• f ^-1(B) – повний прообраз множини F.

• G – сигма-алгебра, породжена борелівськими множинами.

• Борелівська множина – будь-який інтервал

• Борелівська сигма-алгебра містить зліченні об’єднання і перетини інтервалів

Сигма-алгебра – сімейство А ∈ 2^Х, якщо:

• ø ∈ А

• А ∈ А   !А ∈ А

• А₁, А₂,…, А_n,…   А₁∪А₂∪…А_n∪… ∈ А

[ред.]=================

Функція L₀(ω, d) має властивість невід’ємності, якщо:

• L₀(ω, d) ≥ 0

• ∀ ω ∃ d: L₀(ω, d) = 0

L₀(ω, d) = L(ω, d) – - знаходимо в кожному рядочку мінімум. Від решти елементів рядка віднімаємо цей мінімум.

/*якусь інфу просто по функції втрат не знайшов, «шо віжу то пою».*/

Отже, звичайна функція втрат, -- це просто якась функція, яка задана на множині двох параметрів -- ω , d. Фактично, вона показує які втрати несе той хто приймає рішення, коли вибере це рішення, а параметр (ω) стане саме так. Позначається – L(ω,d).

L(ω,d)= - U [σ (ω,d)]