
- •Система прийняття рішень. Загальна задача прийняття рішення.
- •2. 3,4, Параментричні і непараметричні Ср. Лотерейна та Матрична ср. Приклади
- •Непараметричні ситуації прийняття рішень. Приклади.
- •5,6 Перетворення мсср у лсср. Перетворення лсср у мсрр. Еквівалентність
- •6.Перехід від лотерейної до матричної ситуації прийняття рішень та повернення до тієї ж лспр.
- •5.Перехід від матричної моделі до лотерейної
- •11, 12. Перетворення ммср і лмср при стохастичній закономірності
- •1 3. Функція корисності
- •17. Очікувана корисність. Теорема Наймана-Моргенштерна
- •18. Функція втрат. Невід’ємна функція витрат
- •19. Критерій Вальда
- •20. Критерій Севіджа
- •21. Критерій Гуровіця
- •22. Критерій Лапласа
- •23. Система принятия решения и задача решения
- •24. Частково впорядкована множина[ред.]
- •Спеціальні типи частково впорядкованих множин [ред.] Лінійно впорядковані множини [ред.]
- •Цілком впорядковані множини [ред.]
- •Повна частково впорядкована множина [ред.]
- •25. Баєсівський ризик та баєсівське рішення
- •Байєсівський ризик
- •26. Увігнутість баєсівського рішення
- •27,Рандомізація у теорії ігор та теорії рішень.
- •27 Рандомизация и смешанные решения
- •29. Допустима та баєсівська границі у зр зі скінченними просторами
- •33. Побудова байєсівських вирішуючих функції екстенсивним методом
- •35 Лема Неймана –Пірсона.
- •36. Опуклі функції. Нерівність Єнсена
- •39,Системи Підтримки прийняття рішень
- •Класифікація сппр
- •42. Вибірковий простір. Події та їх ймовірності.
- •43 Залежні й незалежні випадкові події,
- •44 Умовна ймовірність та її властивості.
- •45. Случайные величины и их распределения
11, 12. Перетворення ммср і лмср при стохастичній закономірності
Дана
матрична модель, тобто
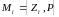 яка
складається з матричної схеми
яка
складається з матричної схеми
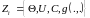 ,
,
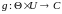 та інформації
.
та інформації
.
Треба
перетворити її в лотерейну модель, тобто
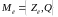 ,
яка
складається з лотерейної схеми
,
яка
складається з лотерейної схеми

 та
інформації
.
та
інформації
.
Треба
побудувати відображення
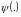 ,
яке задовільняє умову
,
яке задовільняє умову
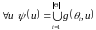
Отже:
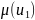 ={
={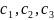 }
}
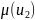 ={
}
={
}
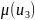 ={
}
={
}
Тепер
треба перенести інформацію. При дії
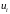 наслідок
наслідок
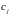 наступає при будь-якому значенні
параметра
наступає при будь-якому значенні
параметра
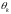 ,
для якого
,
для якого
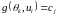 .
Тому розумно встановити між розподілами
.
Тому розумно встановити між розподілами
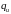 і
таку залежність
і
таку залежність

Оскільки
ми вважаємо, що є тільки одне істинне
значення параметра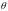 ,
то події
,
то події
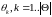 є несумісними, а отже для будь якої їх
суми справедливо
є несумісними, а отже для будь якої їх
суми справедливо
Тому
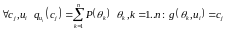
Побудувати модель МСПР по заданій моделі (зі стохастичною закономірністю) ЛСПР
Перевести
МОДЕЛЬ=перевести СХЕМУ+перевести
ІНФОРМАЦІЮ. Схему
переводимо аналогічно до Матрична
ситуація прийняття рішень.
Розподіл на W будуємо так: для кожного
параметру ймовірність його появи
визначатимемо, як добуток ймовірностей
настання відповідних наслідків за
кожної дії P(ω)=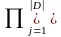 Pdj(g(ω,dj))
Pdj(g(ω,dj))

Побудувати модель ЛСПР по заданій моделі (зі стохастичною закономірністю) МСПР
ZМ ZЛ - так як і в Лотерейна ситуація прийняття рішень
IМ
IЛ:
Pdj(ci)=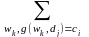 P(ωk)
P(ωk)
dj
D,
ci
C,
j
1..|D|, i=1..|C|
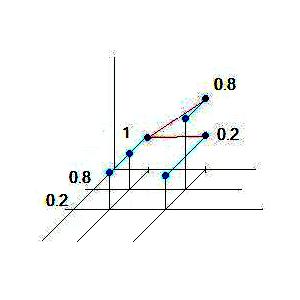
1 3. Функція корисності
Для
будь якого розподілу та будь якої
дійсної функції на множині , існує
позначимо через
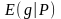 математичне очікування функції
математичне очікування функції
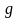 відносно розподілу
відносно розподілу
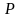 .
Іншими словами :
.
Іншими словами :
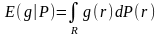
Дійсна
функція
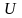 ,
задана на множині
,
задана на множині
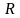 ,
називається функцією корисності, якщо
вона має наступні властивості :
,
називається функцією корисності, якщо
вона має наступні властивості :
Нехай
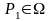 та
та
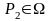 - два розподіли, для яких існує середнє
- два розподіли, для яких існує середнє
 та
та
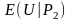 .
Тоді
.
Тоді
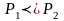 в тому і тільки в тому випадку, коли
в тому і тільки в тому випадку, коли
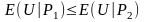 .
Для будь якого доходу
.
Для будь якого доходу
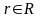 число
число
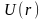 називається корисністю
називається корисністю
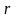 .
.
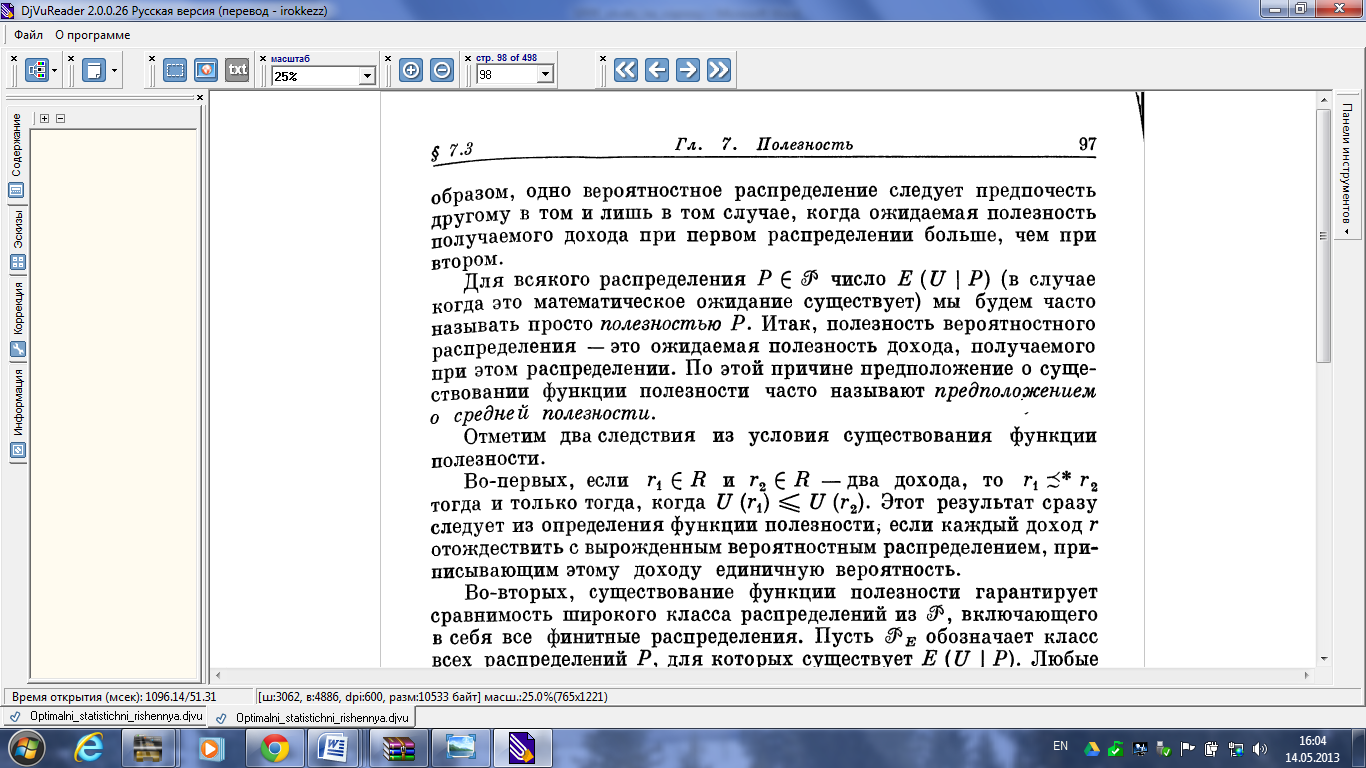
Таким чином, один імовірнісний розподіл варто вибирати ніж інший, тільки в тому випадку, коли очікувана корисність отримуваного доходу при першому розподілі більше, ніж при другому.
Корисність імовірнісного розподілу – це очікувана корисність доходу, отримуваного при даному розподілі.
Існує два важливих наслідки із слідства існування функції корисності :
по
перше, якщо
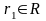 та
та
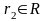 - два доходи, то
- два доходи, то
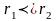 тоді і тільки тоді, коли
тоді і тільки тоді, коли
 .
Цей результат є слідством із визначення
функції корисності.
.
Цей результат є слідством із визначення
функції корисності.
По
друге, існування функції корисності
гарантує спів ставність, широкого класу
розподілів
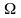 .
.
Відношення
 визначає деяку функцію корисності.
Наступна лема показує, що у випадку
існування функції корисності деякі її
лінійні перетворення є також функціями
корисності.
визначає деяку функцію корисності.
Наступна лема показує, що у випадку
існування функції корисності деякі її
лінійні перетворення є також функціями
корисності.
Лема
1.
Нехай
- функція корисності на
.
Тоді будь яка функція
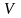 вигляду
вигляду
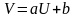 ,
де
,
де
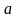 та
та
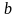 - сталі
- сталі
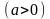 ,
також є функцією корисності.
,
також є функцією корисності.
Доведення.
Для будь якого розподілу
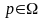 середнє
середнє
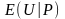 існує тільки тоді, коли існує
існує тільки тоді, коли існує
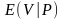 .
Нехай
та
- два розподіли з кінцевими середніми
.
Нехай
та
- два розподіли з кінцевими середніми
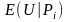 ,
,
 .
Так як
- функція корисності, то
в тому випадку коли
.
.
Так як
- функція корисності, то
в тому випадку коли
.
Але
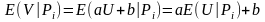
та
в силу позитивності
нерівність
рівносильна нерівності
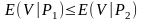 .
Відповідно
- функція корисності.
.
Відповідно
- функція корисності.
14.
У моделі ТПР проектор - функція Π: (S × Βc) → Βu (див. ТПРК1:Лекція2), який показує, як ТПР обирає своє відношення переваг на наслідках і будує відношення переваг на діях. Теорема про очікувану корисність - це спроба описати проектор.
Нехай
можна впорядкувати множину наслідків
C. Наприклад: ![]() .
Така множина наслідків називається доходами.
Тоді можна ввести "грошовий еквівалент".
Тобто співставити наслідкам дійсні
числа. У випадку скінченної множини C
маємо монотонно-зростаючу функцію. За
накладання додаткових умов на множину
наслідків ця функція може бути лінійною.
Ця функція називається функцією
корисності.
.
Така множина наслідків називається доходами.
Тоді можна ввести "грошовий еквівалент".
Тобто співставити наслідкам дійсні
числа. У випадку скінченної множини C
маємо монотонно-зростаючу функцію. За
накладання додаткових умов на множину
наслідків ця функція може бути лінійною.
Ця функція називається функцією
корисності.
Функція корисності позначається через U (utility function). Можна стверджувати, що якщо існує функція корисності U, то існує відповідна їй функція втрат L (loss function), і це однозначна відповідність.
Теорема фон Неймана-Моргенштерна, яка дозволяє побудувати лінійну функцію корисності, була доведена для лотерейної моделі. Тобто її умова має вигляд:
S1 = (Z1,I1)
![]()
![]()
де Qu - розподіл ймовірностей на множині наслідків для дії u.
монотонність функції корисності
Дійсна
функція L, визначена на множині C, є
функцією корисності, або відповідно
втрат, якщо вона є монотонна: ![]()
Якщо C - скінченна, то функцією корисності можуть бути індекси впорядкованої послідовності.
Маємо лотерейну модель непараметричної ситуації, тобто

яка складається з лотерейної схеми
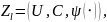

та інформації – розподілу ймовірностей на Cu
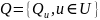
Потрібно побудувати матричну модель, тобто
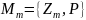
яка складається з матричної схеми
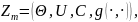
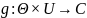
та
інформації P,
тобто розподілу
ймовірностей
на
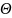 .
.
U
і
C є по умові, треба знайти
,
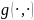 та P.
і
мають
задовольняти умову:
та P.
і
мають
задовольняти умову:
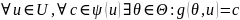
По
іншому кожне значення параметру
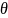 можна приймати як елемент декартового
добутку підмножин наслідків, які
відповідають кожній дії:
можна приймати як елемент декартового
добутку підмножин наслідків, які
відповідають кожній дії:
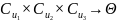
Після
цього можна побудувати розподіл
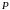 на
на
 .
Подія
полягає в одночасному настанні подій
.
Подія
полягає в одночасному настанні подій
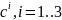 ,
,
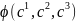 ,
тобто
,
тобто
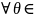
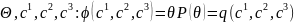
де
q
- розподіл на
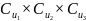
В
нашій задачі ми вважаємо настання
наслідків при різних діях незалежними
подіями, тому природньо дати
 властивість
властивість
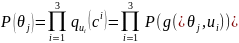
Перехід від матричної моделі до лотерейної можна сформулювати наступним чином. Дана матрична модель, тобто
яка складається з матричної схеми
та інформації P.
Треба перетворити її в лотерейну модель, тобто
яка складається з лотерейної схеми
та інформації Q.
Для
цього переходу треба побудувати
відображення
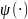 ,
яке задовольняє умову
,
яке задовольняє умову
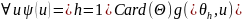
Тепер
треба перенести інформацію. При дії ui
наслідок
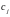 наступає при будь-якому значенні
параметра
наступає при будь-якому значенні
параметра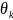 ,
для якого
,
для якого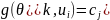 .
Тому розумно встановити між розподілами
.
Тому розумно встановити між розподілами
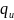 і
таку залежність
і
таку залежність
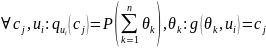
Так
як допускається, що природа знаходиться
в одному певному стані (тобто існує
реально має місце лише одне з значень
параметра
),
то події
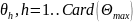 є
несумісними, а отже
є
несумісними, а отже
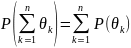
Тому
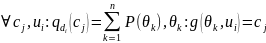
16.Оптимальним рішенням називається те, при якому досягається найкращий середній виграш.
Або те, яке приносить найкращий наслідок з найбільшою ймовірностю.
