42. Вибірковий простір. Події та їх ймовірності.

Випадкова подія — подія, яка при заданих умовах може як відбутись, так і не відбутись, при чому існує визначена ймовірність p (0 ≤ p ≤ 1) того, що вона відбудеться при заданих умовах. Випадкова подія є підмножиною простору елементарних подій.

Те, що випадкова подія має деяку ймовірність проявляється в поведінці її частоти: якщо вказані умови повторити   раз, а подія   відбудеться при цьому   раз, то частота   реалізації події   при великих   стає близькою до  .

Подія може вважатися випадковою лише коли вона може повторитись довільну кількість разів.

Ймовірнісний простір — поняття, введене А. М. Колмогоровим в 30-х роках XX століття для формалізації поняття ймовірності, яке дало початок бурхливому розвитку теорії ймовірностей як строгої математичної дисципліни.

Ймовірнісний простір — це трійка  , де

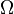•  — довільна множина, елементи якої називаються елементарними подіями, сама множина називається простором елементарних подій;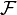

•  — сигма-алгебра підмножин  , званих (випадковими) подіями;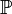

•  — ймовірнісна міра або ймовірність, тобто сигма-адитивна скінченна міра, така що  .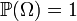

• Розглянемо експеримент з киданням урівноваженої монети. Тоді природним чином задати ймовірнісний простір буде: 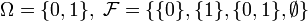  і визначити ймовірність таким чином: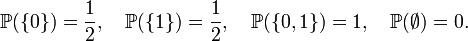

• 

43 Залежні й незалежні випадкові події,

Події В і С називаються залежними, якщо ймовірність однієї з них змінюється залежно від того, відбулась друга подія чи ні. У противному разі події називаються незалежними. Нехай подія А є сумою двох подій В і С. Тоді:

а) якщо події В і С несумісні, то P(A)=P(BC)=P(B)+P(C);

б) якщо події В і С сумісні, то P(A)=P(BC)=P(B)+P(C)-P(BC).

Формули множення ймовірностей для залежних та незалежних випадкових подій.

Нехай подія А є добутком двох подій В і С. Тоді:

а) якщо події В і С незалежні, то P(A)=P(BC)=P(B)*P(C);

б) якщо події В і С залежні, то P(A)=P(BC)=P(B)*P(C/B).

44 Умовна ймовірність та її властивості.

Імовірність події A, визначена за умови, що подія В відбулася, називається умовною і позначається P(A/B). P(A/B)= P(A B) / P(B), P(B) 0. Властивості умовної ймовірності:

1. P(A/B)=0, якщо =

2. P(A/B)=1, якщо =B

3. у решті випадків 0<P(A/B)<1.

45. Случайные величины и их распределения

Основные определения. Результат любого случайного эксперимента можно характеризовать качественно и количественно. Качественный результат случайного эксперимента - случайноесобытие. Любая количественная характеристика, которая в результате случайного эксперимента может принять одно из некоторого множества значений, - случайная величина.Случайная величина является одним из центральных понятий теории вероятностей.

Пусть   - произвольное вероятностное пространство. Случайной величинойназывается действительная числовая функция x =x (w ), w   W , такая, что при любом действительном x  .

Событие   принято записывать в виде x < x. В дальнейшем случайные величины будем обозначать строчными греческими буквами x , h , z , …

Случайной величиной является число очков, выпавших при бросании игральной кости, или рост случайно выбранного из учебной группы студента. В первом случае мы имеем дело сдискретной случайной величиной (она принимает значения из дискретного числового множества M={1, 2, 3, 4, 5, 6} ; во втором случае - с непрерывной случайной величиной (она принимает значения из непрерывного числового множества - из промежутка числовой прямойI=[100, 3000]).

Функция распределения случайной величины. Её свойства

Каждая случайная величина полностью определяется своей функцией распределения.

Если x .- случайная величина, то функция F(x) = F_x (x) = P(x < x) называется функцией распределения случайной величины x . Здесь P(x < x) - вероятность того, что случайная величина x принимает значение, меньшее x.

Важно понимать, что функция распределения является “паспортом” случайной величины: она содержит всю информация о случайной величине и поэтому изучение случайной величины заключается в исследовании ее функции распределения, которую часто называют простораспределением.

Функция распределения любой случайной величины обладает следующими свойствами:

• F(x) определена на всей числовой прямой R;

• F(x) не убывает, т.е. если x₁ 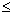x₂, то F(x₁)  F(x₂);

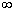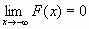• F(- )=0, F(+ )=1, т.е.   и  ;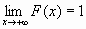

• F(x) непрерывна справа, т.е. 

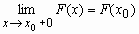
Функция распределения дискретной случайной величины

Если x - дискретная случайная величина, принимающая значения x₁ < x₂ < … < x_i < … с вероятностями p₁ < p₂ < … < p_i < …, то таблица вида

x1	x2	…	xi	…
p1	p2	…	pi	…

называется распределением дискретной случайной величины.

Функция распределения случайной величины, с таким распределением, имеет вид

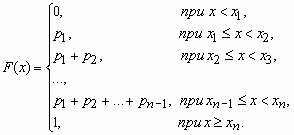
У дискретной случайной величины функция распределения ступенчатая. Например, для случайного числа очков, выпавших при одном бросании игральной кости, распределение, функция распределения и график функции распределения имеют вид:

1	2	3	4	5	6
1/6	1/6	1/6	1/6	1/6	1/6

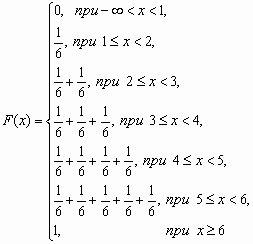
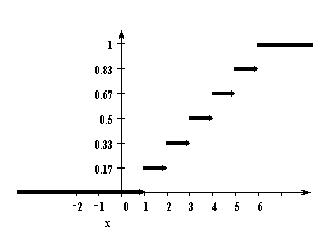
Функция распределения и плотность вероятности непрерывной случайной величины

Если функция распределения F_x (x) непрерывна, то случайная величина x называетсянепрерывной случайной величиной.

Если функция распределения непрерывной случайной величины дифференцируема, то более наглядное представление о случайной величине дает плотность вероятности случайной величины p_x (x), которая связана с функцией распределения F_x (x) формулам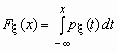и

 и  .

Отсюда, в частности, следует, что для любой случайной величины  .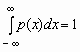

46. Моменти випадкових величин

Початкові та центральні моменти

Узагальненими числовими характеристиками випадкових величин є початкові та центральні моменти.

Початковим моментом k-го порядку випадкової величини Х називають математичне сподівання величини Х ^k:

. (98)

Коли 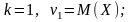коли k = 2, 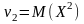і т. д.

Для дискретної випадкової величини Х

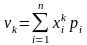; (99)

для неперервної

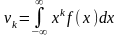. (100)

Якщо Х  [а; b], то

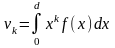. (101)

Центральним моментом k-го порядку називається математичне сподівання від (Х – М(Х))^k:

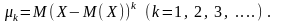(102)

Коли

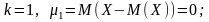
коли k = 2, ;

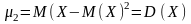коли k = 3,

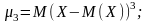
коли k = 4, .

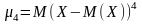Для дискретної випадкової величини

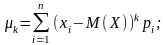(103)

для неперервної

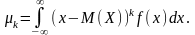(104)

Якщо Х  [а; b], то

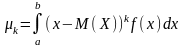. (105)

47 Динамічне програмування дозволяє розв’язувати поставлену задачу на основі об’єднання розв’язків знайдених для допоміжних задач.

При цьому варто зазначити, що термін програмування в даному контексті базується на основі табличного методу, а не написанні комп’ютерної програми. Крім того, якщо в методові розбиття задача ділиться на декілька незалежних між собою задач, кожна з яких вирішується рекурсивно, після чого із розв’язків проміжних задач і формується розв’язок початкової задачі, то динамічне ж програмування, навпаки, застосовується тільки тоді, коли проміжні задачі не є незалежними, тобто різні допоміжні задачі використовують розв’язки одних і тих же підзадач, причому в алгоритмі динамічного програмування кожна проміжна задача вирішується тільки один раз, після чого відповідь зберігається в таблиці. Останнє дає можливість уникати одних і тих же обрахувань кожного разу, коли працюємо з даною підзадачею.

Динамічне програмування, як правило, використовується для задач оптимізації, для яких можлива наявність багатьох рішень. Кожному варіанту розв’язку можна співставити деяке значення і нам потрібно знайти серед них той, який є оптимальним (мінімальним або максимальним). Такий розв’язок називають одним із можливих оптимальних розв’язків. Враховуючи те, що таких розв’язків може бути декілька, їх варто розрізняти від єдиного оптимального рішення.

Процес розробки алгоритмів динамічного програмування можна розбити на 4 нижченаведені етапи:

1. Опис структури оптимального розв’язку.

2. Рекурсивне визначення значення, що відповідає оптимальному розв’язку.

3. Обчислення значення, що відповідає оптимальному рішенню за допомогою методу висхідного аналізу.

4. Отримання оптимального розв’язку на основі інформації, отриманої на попередніх кроках.

Етапи 1-3 складають основу методу динамічного програмування. Етап 4 можна пропустити, якщо треба дізнатись тільки значення, що відповідає оптимальному. На 4 кроці інколи використовується додаткова інформація, отримана із попереднього, щоб полегшити процес побудови оптимального рішення.

49 Принцип оптимальності Белмана

Теорія рішень

Динамічне програмування – собливий метод оптимізації, який використовується при багатокрокових операціях.

Нехай О* - деяка операція, яка розбивається на m послідовних кроків.

Нехай W – міра ефективності цієї операції, припустимо, що вона складається з суми ефективностей на кожному кроці:

Позначимо X=(x₁,x₂,…x_m) – (х_i відповідає і-ому кроку) послідовність дій яка впливає на виграш(ефективність) в цілому і на виграш на кожному кроці або просто керування. Задача зводиться до пошуку такого Х^* при якому W=> max, його будемо називати оптимальним управлінням, а виграш на ньому:

W=max{W(x)}

З першого погляду здається, що дію на кожному кроці треба обирати за принципом максимального виграшу на поточному кроці – А хрін там! Управління повинно обиратись з врахуванням його наслідків у майбутньому – на інших кроках.

Тобто управління на і-ому кроці повинне обиратися таким чином, щоб максимальною була сума виграшів на усіх кроках, що залишились включаючи поточний – Це і є принцип оптимальності Белмана.

50. 11. Теорема Севіджа про суб’єктивну імовірність.