29. Допустима та баєсівська границі у зр зі скінченними просторами

Розглядається спеціальна задача рішення, в якій простір Ω складається з k (k>1) точок, а простір рішень D – з m точок (m>1).

Тобто, D, Ω -- скінченні.

Всі змішані рішення задаються ймовірностями p₁, p₂… p_m. Для задання будь-якого рішення /*(і чистого і рандомізованого )*/ нам достатньо задати ймовірності на кожному з чистих рішеннях, що призводять до такого рішення.

Тоді зрозуміло, що вектор втрат задається так: (позначимо через y(d)):

y(d) = [L(w(₁,d),… , L(w(,d)]

Рішення d є M називається допустимим, якщо не існує іншого рішення d’, при якому L(w_i,d’) =< L(w_i,d),

при i=1,…,k, і що L(w_i,d’) < L(w_i,d) хоча б для одного значення і.

Припустима границя множини G:

Г_п(G)={x є G : не існує y є G, такий що, для всіх i, y_i =< x_i i = 1..k.,

Існує j, y_j < x_j, j=1..k}

Баєсівська границя множини G:

Г_б (G) = {x є G : не існує y, є G, для всіх i, y_i<x_i}

Теорема:

Вектор y(d*) належить баєсівській границі тоді і тільки тоді,

коли існує розподіл ξ параметра W, при якому d* -- баєсівське рішення.

Доведення:

1) припустимо, що d* -- баєсівське рішення при розподілі ξ ={ξ₁, … ξ_k}. І нехай y(d*)=(y*₁,… y*_k). І для всіх інших d, y(d)=(y₁,… y_k). Тоді ξy(d*) =< ξy, оскільки ξk _і >= 0 при i=1..k, і ξ_i > 0 хоча б для одного значення i. Нерівність y_i < y*_i при будь-якому і неможлива /*(бо y* -- баєсівська)*/, тому y(d*) лежить на баєсівській границі G.

2) Тепер нехай y(d*) – точка баєсівської границі. Тоді, а точці y(d*) існує опорна гіперплощина a’x=c така, що всі компоненти вектора a=(a₁… a_і)’ невід’ємні. Поділивши всі компоненти вектора а і сталу с на суму a_і, отримаємо те ж рівняння гіперплощини, але всі компоненти вектора a будуть невід’ємні і в сумі дорівнюватимуть 1. інакше кажучи, його можна буде взяти за ймовірнісний розподіл параметра Ω. З означення опорної гіперплощини, а’у(d*)=c, a’ y>=c для всіх y є G. із цих співвідношень видно, що y(d*) дає найменше значення a’y серед всіх векторів y є G. Отже, d* -- баєсівське рішення а.

Важливий висновок з означень баєсівської/ допустимої границі –

допустима границя – це підмножина баєсівської границі. /*всі допустимі рішення – є баєсівським.*/

30. Два типи спостережень (експериментів) у задачах прийняття рішень (ЗПР).

Існує два типи спостережень у ЗПР :

1. Експеремент проводиться перед тим як прийняти рішення. Досліджуються параметри середовища(параметри що впливають на дії).

y = Function(θ,Ω)

y - результат експеременту для певного параметра. . Де Ω - множина параметрів. ξ - похибка приладу. Сприймайте функцію Function як функцію-експеремент.

2. Експеремент проводиться після приняття рішення. Досліджуються наслідки минулого рішення.

y = Function(c,Ω)

- наслідок з множини наслідків.

У другому типі експеременту наявна дінаміка, тому що поточне рішення приймається спираючись на результат минулого. Тобто дінамічно.

Загальним ризиком від спостереження X і прийняття вирішальної функції називається сума ризику 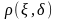й середньої ціни спостереження 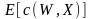. Статистик повинен вибрати спостереження X з деякого класу доступних спостереженню випадкових величин і відповідну байєсівскую вирішальну функцію , яка мінімізує загальний ризик. Виражаючи загальний ризик у вигляді суми ризику вирішальної функції й середньої ціни спостереження, ми неявно використаємо припущення про аддитивності корисностей статистика.

Розглянемо приклад. Припустимо тепер, що ціна спостереження випадкової величини X дорівнює 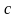, . Статистик може або прийняти рішення, не спостерігаючи X, або заплатити суму й спостерігати X перед ухваленням рішення. При заданому апріорному розподілі 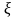запитується, на яку суму с варто погоджуватися статистику?

Для рішення цього завдання треба порівняти мінімальне значення ризику 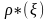без обліку ціни спостереження с, що може бути отримане на основі спостереження X, з мінімальним ризиком 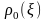, що відповідає байєсівскому рішенню при відсутності спостережень. Функція 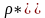вже знайдена. Функція має вигляд

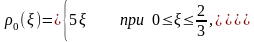(2)

Графіки функцій і зображені на мал. 8.7. Із цього малюнка видно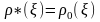, що , якщ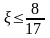о або 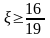. Отже, при значенні апріорної ймовірності , що лежить в одному із цих інтервалів, статистик може досягти й без спостереження X того ж значення ризику, що й при спостереженні X

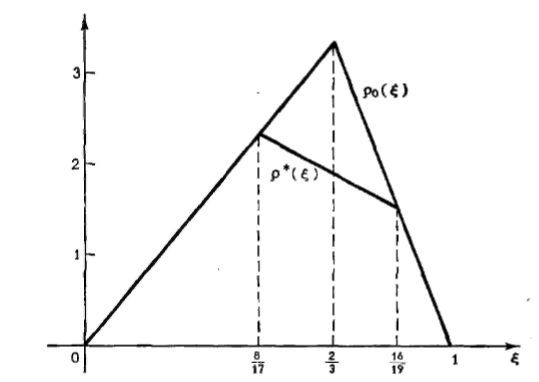
Рис. 8.7. Ризики та із приклада 1.

Якщо ж 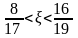, то 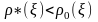за можливість спостереження величини X перед ухваленням рішення статистику треба погоджуватися на будь-яку ціну , таку, що 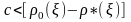, Різницю між ризиками 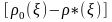максимальна для 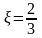, де вона дорівнює .

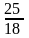У багатьох статистичних задачах рішення спостереження випадкової величини X пов'язане з певними витратами, які повинні враховуватися статистиком при розрахунку ризику від прийняття вирішальної функції, що використає результати спостереження X. Ця обставина грає особливо важливу роль у випадку, коли статистику треба вирішити, яку з декількох випадкових величин краще спостерігати, або вирішити, чи робити спостереження взагалі. Нехай 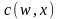позначає ціну спостереження значення х величини X, якщо . 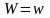Тоді, якщо є о. в. п. випадкової величини W, то середня ціна спостереження дорівнює

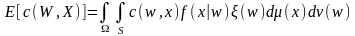
31.

32. Побудова байєсівських вирішуючих функцій нормальним методом.

Апріорний розподіл - розподіл на Ω, який відомо до експерименту.

Апостеріорний розподіл - умовний розподіл на Ω за умови, що ми спостерігали .

Апостеріорний розподіл дає нам додаткову інформацію про параметр і може зменшити байєсівський ризик.

Формула Байєса для обчислення апостеріорного розподілу

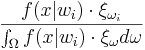
ξω(X)=

-ймовірність настання параметра ω, якщо спостерігали .