2.3.8. Диэлектрическая дисперсия в однородных диэлектриках при наличии двух времен релаксации.
Если диэлектрик имеет диполи двух видов, имеющих разные времена релаксации, то частотная зависимость и будет характеризоваться наличием двух максимумов.
Диэлектрическая
проницаемость изменяется так, что при
выполнении условий
и
,
обнаруживаются перегибы на кривой
.
Максимум определяется условием
;
,
(296)
-
промежуточное значение между
и
.
Диаграмма Коула-Коула будет состоять из двух полуокружностей. Два времени релаксации могут быть вызваны сочетанием двух механизмов релаксации: дипольно-релаксационной и ионно-релаксационной. Если у нас больше двух времен релаксации, то зависимость более сложная.
Если в диэлектрике может быть набор релаксаторов с различными временами релаксации, то они могут создавать непрерывный набор (спектр) времен релаксации, заключающийся в некотором интервале времени. Будем считать такой спектр непрерывным, поэтому можно будет применять интегрирование.
Обозначим
через
относительную вероятность того, что
время релаксации равно
.
Если у всех релаксаторов одно и то же
время релаксации
,
то
.
При наборе времен релаксации
- есть вероятность того, что время
релаксации лежит в интервале от
до
,
причем
.
Действительная и мнимые диэлектрические проницаемости определяются :
,
(297)
,
(298)
При одном времени релаксации они переходят в формулу Дебая. В общем случае необходимо знать функцию .
Практически
из экспериментально полученных
зависимостей
и
можно найти вид функции
.
Диаграмма
Коула-Коула в случае спектра времен
релаксации
представляет собой часть дуги окружности.
Центр этой дуги окружности расположен
под осью абсцисс.
При этом:
,
(299)
где
число в интервале
и характеризующее распределение по
времени релаксации. Зависимость
в
этом случае может быть записана в виде
,
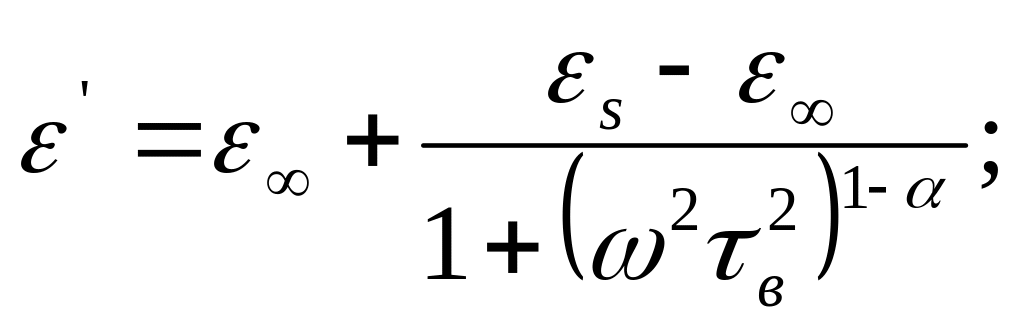(300)
а в виде:
,
(301)
где
- среднее время релаксации.
2.3.9. Температурная зависимость диэлектрических параметров.
Время релаксации является функцией температуры. В частности, при дипольно-релаксационной и ионно-релаксационной поляризации:
,
(302)
С увеличением температуры убывает по экспоненциальному закону.
Проанализируем, как будут изменяться и с изменением температуры для этого подставим (302) в (277) и (279).
,
(303)
,
(304)
1.В
области низких температур
действительная и мнимая части
диэлектрической проницаемости будут
определяться:
и
,
(305)
В области высоких температур
действительная диэлектрическая
проницаемость равна
,
а мнимая часть диэлектрической
проницаемости:
,
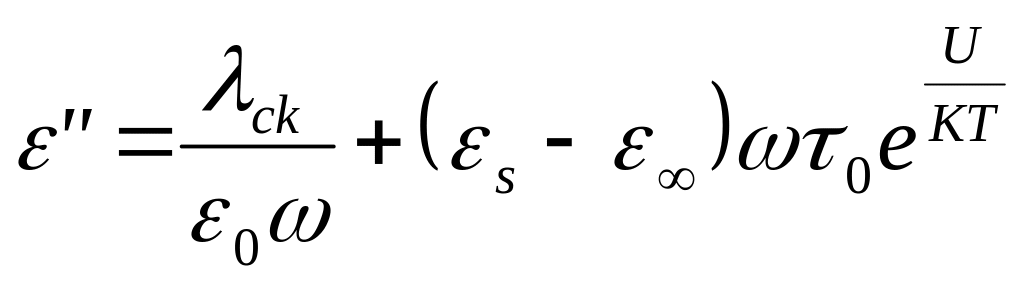(306)
Если
увеличить частоту электрического поля
до
,
при этом (
,
то максимум диэлектрических потерь
сместится в область высоких температур.
Такое смещение максимума позволяет
экспериментально довольно просто
определить энергию активации процесса
релаксации.
;
,
(307)
,
(308)
Поделим соотношение (307) на (308):
,
(309)
Преобразуем (309) и прологарифмируем правую и левую часть:
,
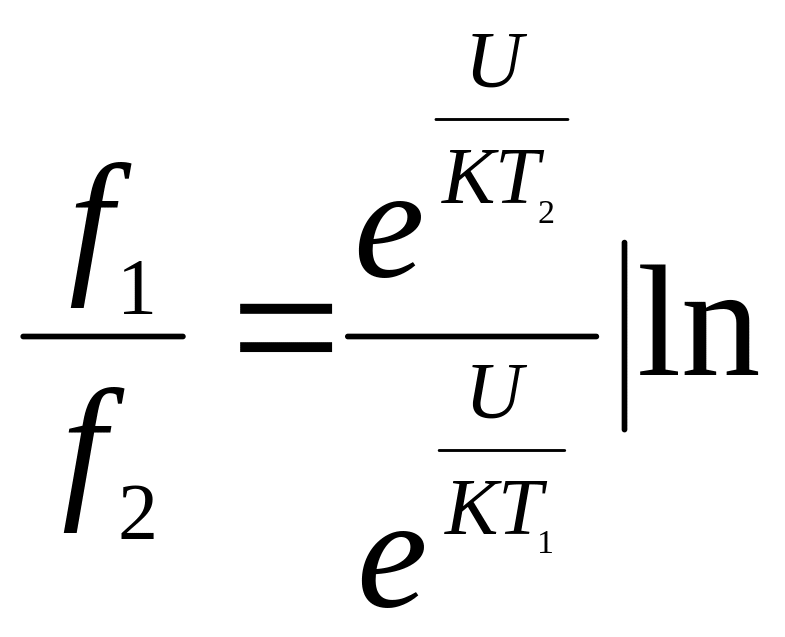(310)
и найдем выражение для энергии активации:
,
(311)