Глава 2. Диэлектрик в переменном электрическом поле

Электроны, ионы и диполи, находящиеся в диэлектрике под действием внешнего периодически изменяющегося электромагнитного или электрического поля могут смещаться относительно своего первоначального положения, обуславливая поляризацию диэлектрика.

2.1 Микроструктура диэлектрической постоянной в поле световой волны

Для описания поведения электрона в поле световой волны используют модель упруго-связанного электрона (раздел 1). Предположим, что электромагнитная волна распространяется по оси х, а напряженность электромагнитного поля изменяется по оси z . На электрон в поле световой волны действует электрическая сила:

F_э,=eE_х , (122)

которая смещает его от первоначального состояния, упругая сила связи электрона с атомом :

F_г = -Кx , (123)

и сила лучистого трения :

, (124)

Движение упруго-связанного электрона в электрическом поле световой волны будет описываться уравнением Ньютона:

, (125)

Подставим соотношения (123) и (124) в (125) и получим:

, (126)

Изменение напряженности поля световой волны вдоль оси х определяется соотношением:

, (127)

При z=0

, (128)

Волна распространяется по оси x, а напряженность по оси z. Второй член отбросим, так как атом фиксирован в одной точке.

, (129)

Необходимо учесть магнитную энергию электромагнитного поля

и в уравнение (129) записать силу Лоренца , но величина мала, и ей можно пренебречь.

Предположим, что электрон совершает вынужденные колебания с той же частотой, что и напряженность поля в световой волне

, (130)

Найдем первую, вторую и третью производную смещения атома по времени:

, (131)

, (132)

, (133)

Подставим найденные соотношения (132), (133) в (129) и получим:

, (134)

Обозначим выражение:

, (135)

тогда амплитуда вынужденных колебаний электрона будет равна:

, (136)

Если бы не было не электрического поля, ни лучистого трения, тогда , (137)

и электрон совершал бы собственные колебания под действием упругой силы, которая возникает в атоме за счет тепловой энергии.

Смещение атома при этом описывается выражением:

, (138)

где - частота собственных колебаний электрона и а- амплитуда колебаний.

Найдя первую и вторую производную:

, (139)

подставив соотношение (139) в (137) получим:

, (140)

Из (140) следует, что собственная частота электрона связана с коэффициентом упругой связи и его массой соотношением:

, (141)

Подставляя (141) в (136) получим выражение для амплитуды вынужденных колебаний:

, (142)

Тогда смещение атома согласно (130), (142) будет определяться выражением:

(143)

Дипольный момент атома будет определяться величиной смещения электрона под действием электрического поля и равен p=ex

, (144)

Сопоставим формулу (144) с (8) получим:

, (145)

тогда диэлектрическая проницаемость будет равна:

, (146)

Подставляя (135) в (146) и разделив числитель и знаменатель дроби на массу электрона m получим:

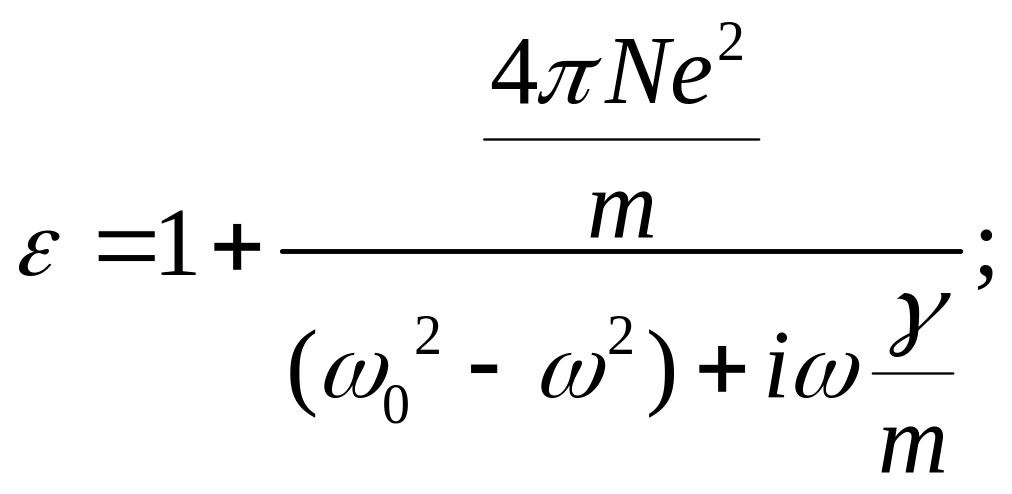, (147)

где соответствует выражению плазменной частоты возведенному в квадрат.

Обозначим и получим:

, (148)

Проанализируем полученное выражение. Отделим мнимую и действительную часть соотношения (148) умножив числитель и знаменатель дроби на комплексно-сопряженное слагаемое

, (149)

Приведем дробь к наименьшему знаменателю и сократим подобные члены:

, (150)

Диэлектрическая проницаемость представляет собой комплексную величину и определяется соотношением:

, (151)

где действительная часть равна:

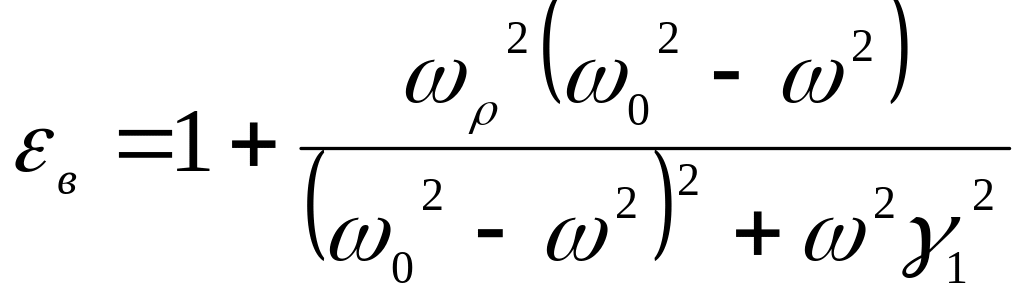, (152)

мнимая часть диэлектрической проницаемости:

, (153)

В общем виде:

, (154)

Если не было бы трения , то не было бы и мнимой части. Выясним физический смысл и . Будем использовать для этого первое уравнение Максвелла:

, (155)

Используя известные соотношения:

, (156)

, (157)

, (158)

, (159)

получим, что:

, (160)

, (161)

Если j=0, то

, (162)

С учетом соотношения (161) следует, что:

(163)

Таким образом, мнимая часть диэлектрической проницаемости обусловлена электропроводностью системы и характеризует превращение электромагнитной энергии в тепловую энергию в соответствии с законом Джоуля - Лентца .