9) Всякое каким-то образом выделенное множество объектов, которые могут отличаться друг от друга значением некоторой определенной характеристики, называется генеральной совокупностью.

Часть генеральной совокупности, случайным образом отобранная для наблюдений, называется случайной выборкой или, для краткости, выборкой.

Число элементов выборки называется ее объемом.

Репрезентативность выборки - основное свойство выборки, способность ее воспроизводить и представлять характеристики ГС. Выборка должна быть моделью ГС. Это свойство воспроизводить статистическую структуру ГС в отношении изучаемых характеристик. Она является основным условием формирования и проектирования выборки.

В идеале выборка должна быть репрезентативна по всем изучаемым характеристикам.

Вариационный ряд — упорядоченная по величине последовательность выборочных значений наблюдаемой случайной величины

равные между собой элементы выборки нумеруются в произвольном порядке; элементы вариационного ряда называются порядковыми (ранговыми) статистиками; число λ_m =m / n называется рангом порядковой статистики 

Вариационный ряд используется для построения эмпирической функции распределения. Если элементы вариационного ряда независимы и имеют общую плотность распределения f, то совместная плотность распределения элементов вариационного ряда имеет вид

Имеются данные о количестве студентов в 30 группах физико-математического факультета:

26	25	25	26	25	23
23	24	19	23	20	19
22	24	24	23	20	23
24	19	21	18	21	18
20	18	18	21	15	15

Найти вариационный ряд количества студентов в группах и размах варьирования. Построить полигон частот.

Решение. Записывая исходные данные в порядке возрастания, составим вариационный ряд:

	15	18	19	20	21	22	23	24	25	26
	2	4	2	4	3	1	5	4	3	2

Размах варьирования  .

Для построения полигона частот обозначим на оси абсцисс возможные значения признака, а на оси ординат соответствующие частоты   и полученные точки соединим отрезками.

Рис. 96

Характеристики выборки:

• Качественная характеристика выборки – кого именно мы выбираем и какие способы построения выборки мы для этого используем.

• Количественная характеристика выборки – сколько случаев выбираем, другими словами объём выборки.

10) Основными параметрами генеральной совокупности являются математическое ожидание (генеральная средняя) М(Х) и среднее квадратическое отклонение s. Это постоянные величины, которые можно оценить по выборочным данным. Оценка генерального параметра, выражаемая одним числом, называется точечной.Точечной оценкой генеральной средней является выборочное среднее  .Выборочным средним называется среднее арифметическое значение признака выборочной совокупности.

Если все значения x₁, x₂,..., x_n признака выборки различны (или если данные не сгруппированы), то:

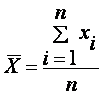
Если же все значения признака x₁, x₂,..., x_n имеют соответственно частоты n₁, n₂,..., n_k, причем n₁ + n₂ +...+ n_k = n (или если выборочное среднее вычисляется по вариационному ряду), то

В том случае, когда статистические данные представлены в виде интервального вариационного ряда, при вычислении выборочного среднего   значениями вариант считают середины интервалов.

Интервальная оценка

Интервальная оценка включает в себя два компонента:

• Интервал в котором ожидается обнаружить оцениваемый параметр генеральной совокупности;

• Вероятность обнаружения параметра в данном интервале.

1. Определить какой статистикой необходимо пользоваться и найти соответствующую таблицу.

2. Задавшись некоторой доверительной вероятностью, по выбранной таблице для заданной вероятности определить такое Дельта, чтобы в пределах Альфа +- дельта лежало 95% площади кривой.

3. Из ген совокупности извлекается случайная выборка и вычисляется значение статистики А. таким образом А +- Дельта и есть искомый 95%-й доверительный интервал.