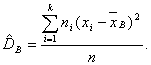15. Функция и плотность распределения вероятности.
F(x) = Р{Х ≤ х}
Функция распределения полностью характеризует случайную величину, однако, имеет один недостаток. По функции распределения трудно судить о характере распределения случайной величины в небольшой окрестности той или иной точки числовой оси.
Плотностью распределения вероятностей непрерывной случайной величины Х называется функция f(x) – первая производная от функции распределения F(x).
Смысл плотности распределения состоит в том, что она показывает как часто появляется случайная величина Х в некоторой окрестности точки х при повторении опытов.
16. Мат. Ожидание и дисперсия непрерывной случайной величины.
Математическое ожидание непрерывной случайной величины X, возможные значения которой принадлежат всей осиОх, определяется равенством:
Дисперсия непрерывной случайной величины X, возможные значения которой принадлежат всей оси Ох, определяется равенством:
17. Равномерное распределение.
В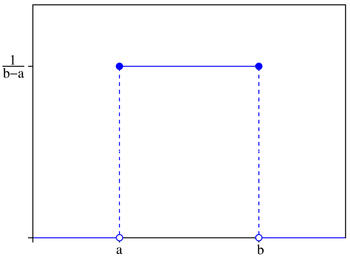
теории
вероятностей случайная
величина имеет дискретное равномерное
распределение,
если она принимает конечное число
значений с равными вероятностями.
Непреры́вное равноме́рное распределе́ние — в теории вероятностей - распределение случайной вещественной величины, принимающей значения, принадлежащие интервалу [a, b], характеризующееся тем, что плотность вероятностина этом интервале постоянна.
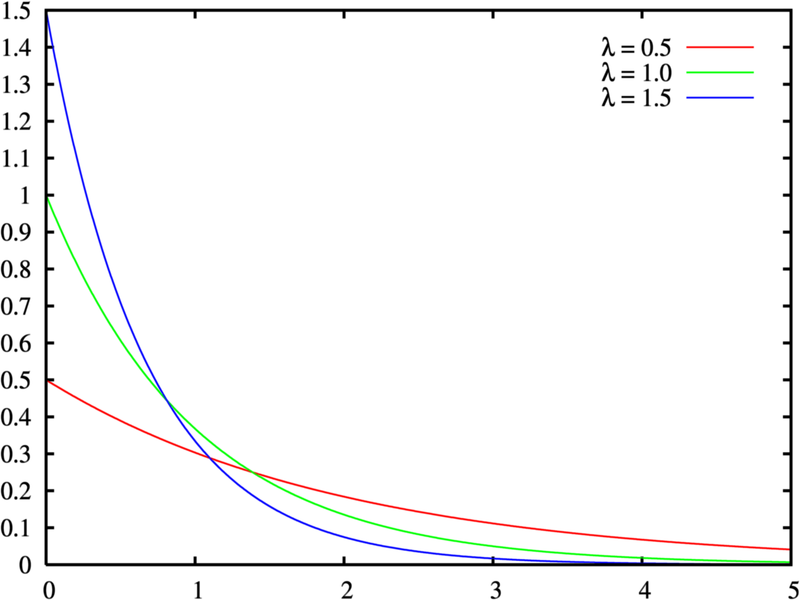
18. Экспоненциальное распределение.
Экспоненциальное распределение — абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события.
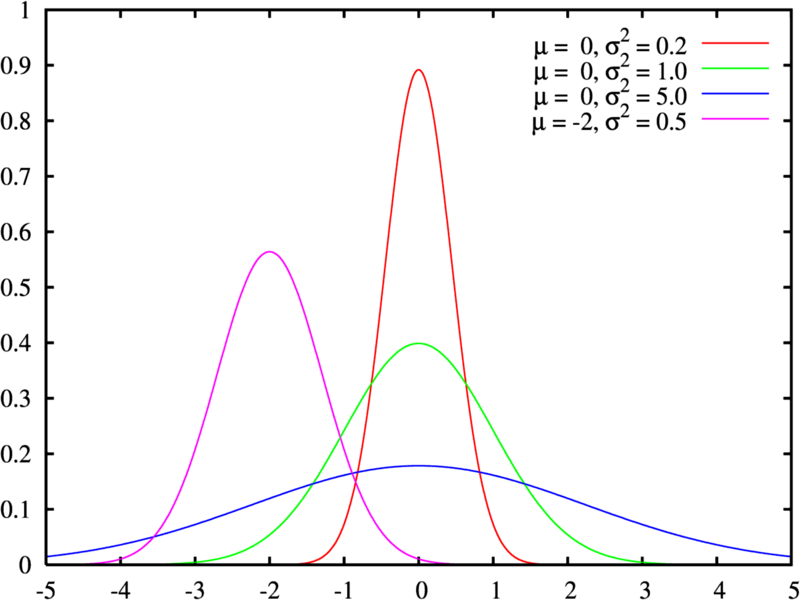
19. Нормальное распределение.
Нормальным называют распределение, при котором намименьшие и наибольшие значения имеют наименьшую плотность распределения вероятностей, а самую большую плотность имеют средние значения.
20. Выборочная и генеральная совокупности. Типы выборок. Статистическое распределение выборки.
Выборочной совокупностью называют совокупность случайно отобранных объектов.
Генеральной совокупностью называют совокупность всех объектов, из числа которых производилась выборка.
Объемом совокупности называют число объектов в совокупности.
Типы:
|
|
21. Эмпирическая функция распределения.
Эмпирической функцией распределения называют функцию, определяющую для каждого значения х относительную частоту события Х<х: f(x)=nx/n
22. Полигон и гистограмма.
Полигоном частот называют ломаную, отрезки которой соединяют точки (x1n1), (x2n2) и т.д.
По оси x откладывают варианты, по оси y – частоты.
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основанием которых служат частичные интервалы длиной h, а высоты равны отношению ni/h
23. Несмещенные и эффективные состоятельные оценки.
Несмещенной называют статистическую оценку, математическое ожидание которой равно оцениваемому параметру.
Эффективной называют статистическую оценку, которая имеет наименьшую возможную дисперсию.
Состоятельной называют статистическую оценку, которая при n→∞ стремится по вероятности к оцениваемому параметру.
24. Выборочная средняя.
Выборочной средней называют среднее арифметическое значение признака выборочной совокупности.
Если все значения признака выборки различны, то
если же все значения имеют частоты n1, n2,…,nk, то
Выборочная средняя является несмещенной и состоятельной оценкой генеральной средней.
25. Выборочная дисперсия.
Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения .
Если все значения признака выборки различны, то
если же все значения имеют частоты n1, n2,…,nk, то
